正确理解热力学第三定律

苏许辉

(宁波中学 浙江 宁波 315100)

高中人教版《物理·3-3》主要包括热学的相关内容.热力学的三大定律是热学的基础，课本对热力学第一定律和第二定律已经有了比较详细的介绍，而对第三定律只有简单的一个表述：任何系统都不能通过有限的步骤使自身温度降低到绝对零度，即绝对零度不可达到.

在教学的过程中，每次讲到这里，都有不少同学对此充满好奇，问：为什么绝对零度不能达到呢？由于受到高中物理知识广度和深度方面的限制，许多老师和学生习惯于从分子动理论出发，对热力学第三定律——绝对零度不能达到的原因进行了较片面地理解，不少老师也都是按下面的方法进行解释的.

1 依据分子动理论对“绝对零度不能达到”进行解释

根据经典热力学，温度是物体分子热运动平均动能的标志，它们之间的关系可以表达为

(1)

式中，k为玻尔兹曼常量；i为分子各种运动自由度数，包括分子的平动自由度、转动自由度、振动自由度.

从(1)式可见，由于物体内分子无规则运动的平均能量与温度成正比，因此如果绝对零度能够达到，则分子的平均动能为零，分子将处于完全静止的状态，而这与分子动理论对分子的热运动的描述：“物体是由大量分子组成的，分子永不停息地做无规则运动”相矛盾.

上面依据分子动理论的知识，从经典热力学做出的解释好像能够说明绝对零度为什么不能达到.但是随着实践的进展，经典热学理论已显示出它的局限性：如果在绝对零度下粒子是静止不动的，那么它的速度为零，这时它的位置就是确定的.这样的话，位置和速度两者的值我们都知道了，这不符合海森伯的不确定原理——它只允许知道一个.所以，近代物理的量子理论对经典热力学作了修正，指出：即使温度能够达到绝对零度，分子也不会完全静止，因为分子还具有“零点能”.并且，零点能的存在已经从实验中得到了证实.

可以看出，依据分子动理论的相关内容，从经典热力学出发，认为分子在绝对零度会静止不动的观点是站不住脚的，以此来解释绝对零度不能达到就有一定的局限性.

2 热力学零度不能达到的原因

现从能斯特定理出发，来证明绝对零度为什么不可达到[1].

首先考虑降温的手段，即考查经历何种过程降温最有效.显然，放热降温当然有效，但又必须有更低温度的热源，这是不实际的.因此，只有绝热降温是可取的方式.这又有两种选择：可逆或不可逆.我们来分析这两种方式.假定以(T，y)为独立参数，y可能是实验可控的体积、压强等.

对于可逆过程，随着温度的增加系统的熵亦增加.在S-T图(图1)上，假定物体系由y1线上的一点A经历绝热可逆过程(熵不变，沿水平线)到达y2线的B点.两状态的温度分别记为TA和TB.

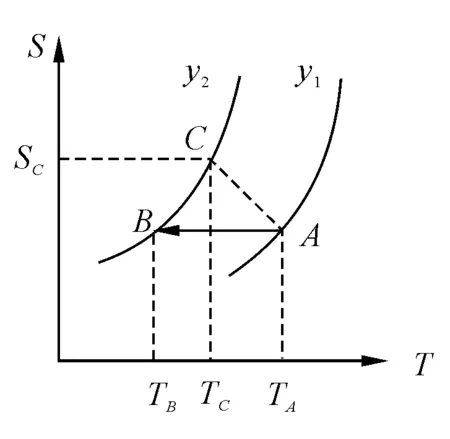
图1 物体系熵随温度T和y的变化趋势

如果由A经历不可逆绝热过程(熵增加)到达y2线，则应到达熵更大的一点C，显然有

TC>TB

可见，可逆过程降温更为有效，即绝热可逆过程降温是最有效的途径，故而我们只讨论绝热可逆过程.

熵的计算公式

(2)

量子理论与实验都给出，在极低温度下，非金属定容摩尔热容CV∝T3，金属CV∝T，所以

上述(2)式在T→0时收敛.并且，当物体系由A(TA，yA)经绝热可逆过程(熵不变)至B(TB，yB)时，有

SA=SB

由能斯特定理

S(0,yA) =S(0,yB)

因而

(3)

如果

TA>0

则有

亦必有

TB>0

即绝热可逆过程不能将温度降至绝对零度.

因此，任何有限步骤都不能将体系的温度降至绝对零度.

3 展望

热力学第三定律虽明确指出，绝对零度不可能达到，但这并没有阻止人们向这个最冷的极地逼近.早在1926年，德拜和吉奥克用磁冷却法达到了10-3K.后来又有人攻破了10-6K.1995年，科罗拉多大学和美国国家标准研究所的两位物理学家爱里克·科内尔和卡尔威曼成功地使一些铷原子达到了令人难以置信的温度，即2×10-8K.2003年，科学家更获得5×10-10K.当然，我们相信科学家一定还可以达到更低的温度.然而，人们发现，温度越低，进一步逼近绝对零度就更加困难.这所有的努力都说明热力学第三定律的正确，即绝对零度是低温的极限，是不可能达到的.

参考文献

1 王竹溪. 热力学. 北京:高等教育出版社,1955.355～365