数学分析教学中的软件应用实验设计
闫 峰,张艳霞
(邯郸学院 数学系,河北 邯郸 056005)
1 引言
在传统的数学分析教学中,基本上采用教师主要讲解的灌输式教学方法,学生的积极性不高,对一些知识点也缺乏直观的认识。现行的一种较先进的教学手段——计算机辅助教学(Computer Assisted Instruction)简称CAI,是教师将计算机用作教学媒体,学生通过与计算机的交互作用进行学习的一种教学形式,它能充分利用计算机存储量大,快速处理图象、声音、动画等功能,产生出图文并茂,声色俱全的视听效果,达到改善学习环境、优化教学效果的目的,完成传统教学方式难以实现的教学任务。如何在数学分析的教学和学习中,正确使用CAI技术手段(尤其是数学软件)是教师迫切需要考虑的一个问题。
鉴于《数学实验》课程的一些成功经验,作者在数学分析的部分授课过程中尝试引入《数学实验》的教学思想,借助于CAI系统,主要利用MATLAB数学软件对某些内容设计不同的实验方案,每个实验围绕可引起学生兴趣的问题展开,教学生使用若干方法来解决问题,在解决问题中熟悉这些方法,得出相应的结论。这些尝试使学生对抽象数学有了一个直观的了解,激发了学生的学习积极性,提高了他们的动手能力和探索的兴趣,并对MATLAB数学软件也有了初步的了解和掌握。下面仅介绍教学中的几个方面。
2 利用MATLAB软件的数据可视化加强学生的空间想象力
数学分析教学过程中,经常会见到一些复杂的图像、图形,比如螺旋线、空间中的二次曲面、一些极坐标表示的曲线、以及一些物体运动的轨迹等,一般数学课堂要求学生发挥“空间想象力”。实践证明,多数学生一学期下来后,对什么是马鞍面,什么是椭圆双曲面等仍有读天书的感觉,让数学软件直观地演示一下这些图形,将“空间想象力”变为“直观观察力”则更为现实有效,教学效果也更明显。
实验1.空间中二次曲面的图形。
1)提出问题:根据空间解析几何的知识考虑二元函数 z=xy,(x,y )∈R2[1]91的图形(尽管函数表达式很简单,但图形不好想象)。
2)利用MATLAB软件绘出它的图形:
[x,y]=meshgrid(-4:0.125:4); >> z=x.*y;>> mesh(x,y,z)
使学生对此函数的图形有一个直观的认识。(如图1)
3)利用MATLAB软件绘制更为复杂的函数图形。

图1
并在重积分部分,也通过作图观察变量的取值范围,教学效果非常好。
3 MATLAB软件在积分运算方面的应用
由数学分析的知识:有理函数都能积分,相关理论已经很完备,但其计算往往非常复杂,耗费学生很多时间。可否将这些繁琐计算留给计算机完成?这些问题的解决有待于我们对现行课程教材体系进行新的思考和创新。
实验2.简化有理函数积分的计算过程。
2)利用MATLAB软件计算上述积分:syms x;>> int((-x^2-2)/(x^2+x+1)^2)
执行上述命令后,马上显示结果:
1/3*(-3*x-3)/(x^2+x+1)-4/3*3^(1/2)*atan(1/3*(2*x+1)*3^(1/2)),说明软件的快捷和方便;
3)后继内容中进一步探讨MATLAB在定积分、数值积分中的应用。
4 泰勒级数逼近分析器的应用
我们知道:若一元函数f(x)在点x0具有任意阶导数,且 ∀x:|x −x0|<r,f(x)在点x0的泰勒公式的余项Rn(x)当n→∞时极限为0,则f(x)在给定区间 (x0− r, x0+ r )内等于它的泰勒级数的和函数。[1]53那么泰勒多项式是如何逼近函数f(x)的?利用MATLAB软件提供的一个进行数学分析的可视化界面:泰勒级数逼近分析界面,可方便地观察函数f(x)在给定区间上被n阶泰勒多项式逼近的情况,使学生对级数理论的认识更加深刻。
实验3.函数的泰勒级数展开。
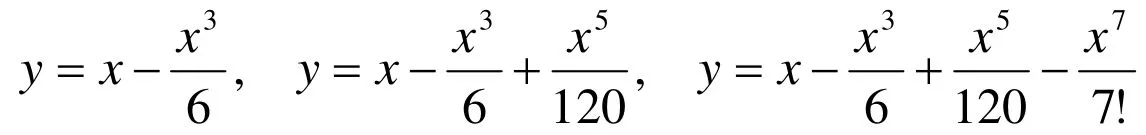
2)通过图形观察这些多项式函数与正弦函数y=sinx有什么关系?得出结论:上述多项式函数分别是正弦函数的3阶、5阶、7阶泰勒多项式。
3)进而观察泰勒多项式逼近正弦曲线的情况。
4)利用泰勒级数逼近分析界面说明问题(如图2)。
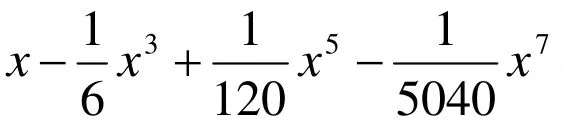
5)任意改变被逼近函数表达式、区间范围或泰勒多项式的阶数均可得到类似结果。
5 二元函数极限存在性的判别
相比一元函数在某点极限的存在性,二元函数重极限和累次极限的存在性就复杂多了,这也是教学中的难点所在。可通过图形猜测二元函数重极限是否存在。
图2
1)提出问题:猜测极限的存在性。
2)绘制二元函数的图形(图3)。
3)通过观察图3,利用旋转按钮可以看出:当(x,y)充分接近于原点时,函数值充分接近于0即函数在(0,0)点的极限存在。
4)理论上严格证明。
6 函数列一致收敛的直观演示
函数列的一致收敛是数学分析教学中的难点,也是重点,学生理解较为困难,往往很难分清函数列收敛和一致收敛的本质区别。
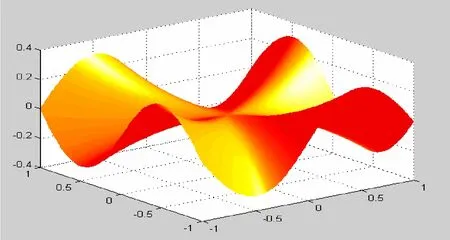
图3
实验5.分别讨论函数列 {f (x)}={nx2e−nx},x∈[0,5]和{g(x)}={n2xe−n2x2},x ∈[0,1]的收敛性和一致nn收敛性。
2)学生总结函数列在给定区间一致收敛时的图形显示情形。
3)利用 MATLAB软件编程分别绘制{fn(x )}和{gn(x)}当n分别取1,2,3,…,8时的函数图形,以说明函数列的变化趋势。
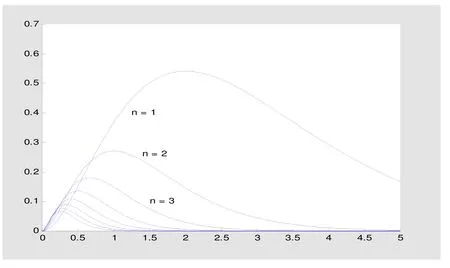
图4 {f(x)} n 的图形
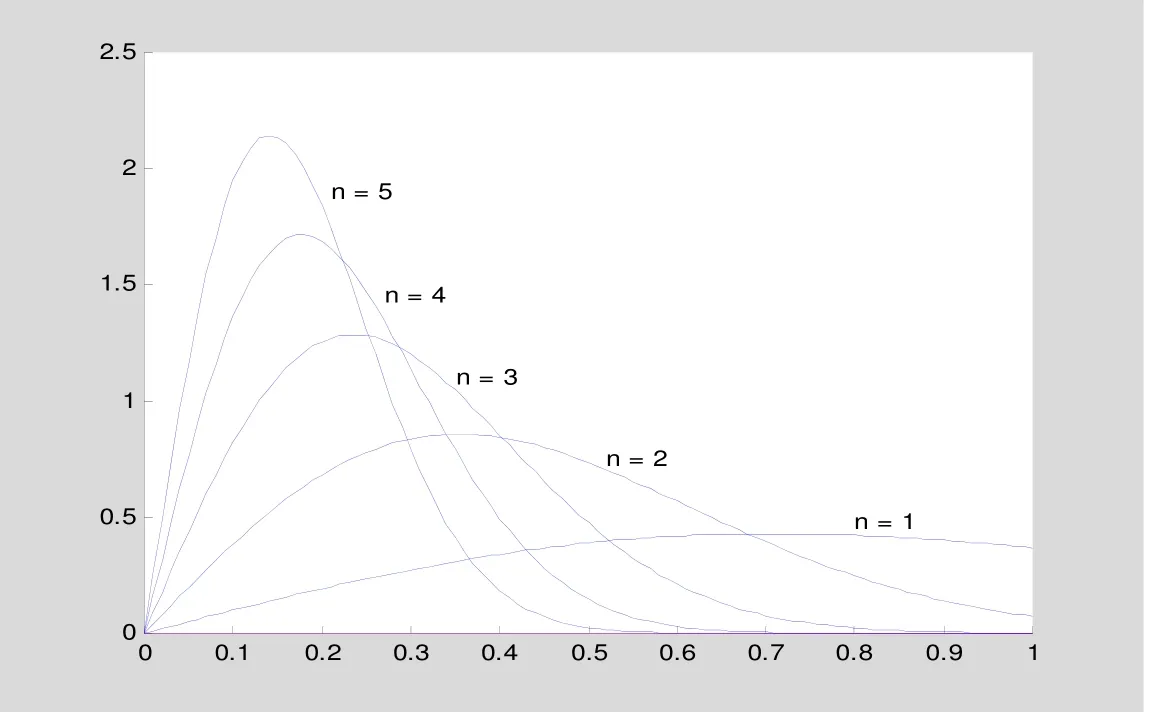
图5 {g(x)} n 的图形
本文仅讨论了利用MATLAB软件在数学分析课程教学中进行的CAI教学的几个方面,在实际教学中还在不断探索,课下学生可自己动手做数学实验,效果较好。
[1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2003.
[2]李尚志.数学实验[M].北京:高等教育出版社,2008.

