基于小波分析理论的文本加密

李骁一

（大连东软 信息学院，辽宁 大连 116023）

1 引言

我们知道随着互联网技术的发展，网络信息的传输在人们的日常生活中变得越来越重要。随之而来的是信息传输的安全问题也就越来越引起人们的关注，特别是对于普通的互联网用户其信息的安全一直没有一种简单可行的保护方法。

小波分析是建立在泛函分析，调和分析、傅里叶分析基础上的时频原子。其理论和方法在信号处理、数据压缩、图像处理[1]285-287，[2]32-34等方面有着广泛的应用。针对上述问题，本文提出利用小波分析及水印技术的相关知识来探讨将文本信息加密嵌入相应的信息载体中进行传输，从而对所要传输的文本起到隐藏保护作用。

2 概述

小波分解[3]35-38，[4]19-21方法是一种窗口大小（即窗口面积）固定，但其形状可改变，时间窗和频率窗都可改变的时频局域化分析方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，所以被称为“数学显微镜”。正是这种特性，使小波变换具有对信号的自适应性。

小波变换可以同时在时域和频域上分析信号的局部特性。平方可积函数f(t)∈L2(R)的连续小波变换定义为：

在本文中，主要用到的是 Matlab中小波工具箱的二维离散部分。我们只给出这里用的两个函数 dwt2和idwt2[7][8]做简单的介绍：

2.1 dwt2函数

函数功能：二维单尺度小波变换

语法格式：（1）[cA，cH，cV，cD]=dwt2(X，‘wname’)；（2）[cA，cH，cV，cD]=dwt2(X，Lo_D，Hi_D)使用说明：dwt2使用指定的小波(‘wname’)或者分解滤波器(Lo_D，Hi_D)进行二维单尺度小波分解。

格式（1）根据输入矩阵X进行小波分解，计算低频矩阵cA和高频系数矩阵cH（水平方向）、cV（垂直方向）、cD（对角方向）；

格式（2）基于指定的小波分解滤波器计算二维小波分解系数。其中，Lo_D是分解低频滤波器， Hi_D是分解高频滤波器。Lo_D和Hi_D必须具有相同的长度。

函数说明：对于图像分解，其算法类似于一维分解比较。二维小波函数和尺度函数算法是通过一维小波函数和尺度函数的张量积得到的。二维离散小波变换是尺度j的低频系数分解为4个部分：尺度j-1的低频部分，以及水平、垂直、对角等3个方向的高频部分。

2.2 iwdt2函数

函数功能：二维单尺度小波逆换。

语法格式：（1）X= idwt2(cA，cH，cV，cD，‘wname’)；

（2）X=idwt2(cA，cH，cV，cD， Lo_R，Hi_R)；

（3）X=idwt2(cA，cH，cV，cD，‘wname’，s)；

（4）X=idwt2(cA，cH，cV，cD， Lo_R，Hi_R，s)

使用说明：idwt2命令使用给定的小波(‘wname’)或者小波重构滤波器(Lo_R和Hi_R)进行单尺度二维小波重构。

格式（1）使用小波‘wname’，基于低频矩阵cA和高频水平方向矩阵cH，垂直向矩阵cV和对角矩阵cD，计算单尺度重构低频系数矩阵X；

格式（2）使用的是指定滤波器。Lo_R是重构低通滤波器，Hi_R是重构高通滤波器；

格式（3）和（4）使用语法idwt2(cA，cH，cV，cD，‘wname’)返回尺度s的中间部分。

本文是利用上述两个二维离散分解合成函数以及turn5工具和相应的嵌入算法来完成相应的加密和解密工作。

3 水印技术原理

水印的基本原理和算法通用的水印技术[9]包含两个方面：水印的嵌入和水印的提取或检测（图1和图2所示）

图1 水印信号嵌入

图2 水印信号提取

而我们提出的文本加密嵌入的基本原理和算法，和上述方法类似就是将文本转化为相应的矩阵信息嵌入某个信息载体，将此信息载体连同文本信息一同传输来达到隐蔽的目的。

4 文本的信息转化加密与解密

4.1 Turn5的简介

Turn5是一数据以及字符转换工具，其功能有进制转换、字符转换、逻辑运算等几种在计算机运算中较为常见的转化。

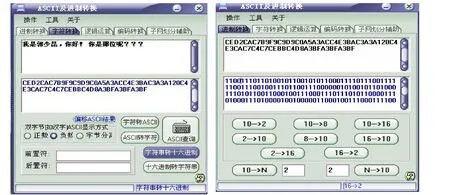
图3 文本信息转化为数值信息

图3是turn5将文本信息转化为数值信息的过程，先在字符转换工具中文本转化为十六进制字符，然后在进制转换工具中将十六进制字符转化为二进制数据。

图4是图3的逆过程是把在图像中分离出的二进制信息，在turn5中转化为文本信息。

4.2 文本转化加密与解密

所谓的文本的信息加密，就是将文本信息转化为我们能够处理的数值信息。在这里我们借助于 turn5这个字符进制转换工具，由于Matlab是对矩阵进行处理运算的，所以我们首先将文本信息在turn5中转化并写成一个纯数值的文本，然后用Matlab中的fopen，fscanf函读取并写成矩阵嵌入图像高频信息矩阵中，经加密处理后重构图像，从而隐藏文本信息。

第一种加密及解密方法：其具体加密步骤如下：

（1）第一步：将文本信息在turn5中转化为二进制数值信息；目的是为了在Matlab中使用函数fopen，fscanf读成矩阵后便于处理。

（2）第二步：用dwt2函数对图像做小波分解变换，分离出图像中的高频矩阵。为将要嵌入的二进制数值信息数据提供存储空间。

（3）第三步：将第一步转化的文本信息嵌入到高频矩阵中。

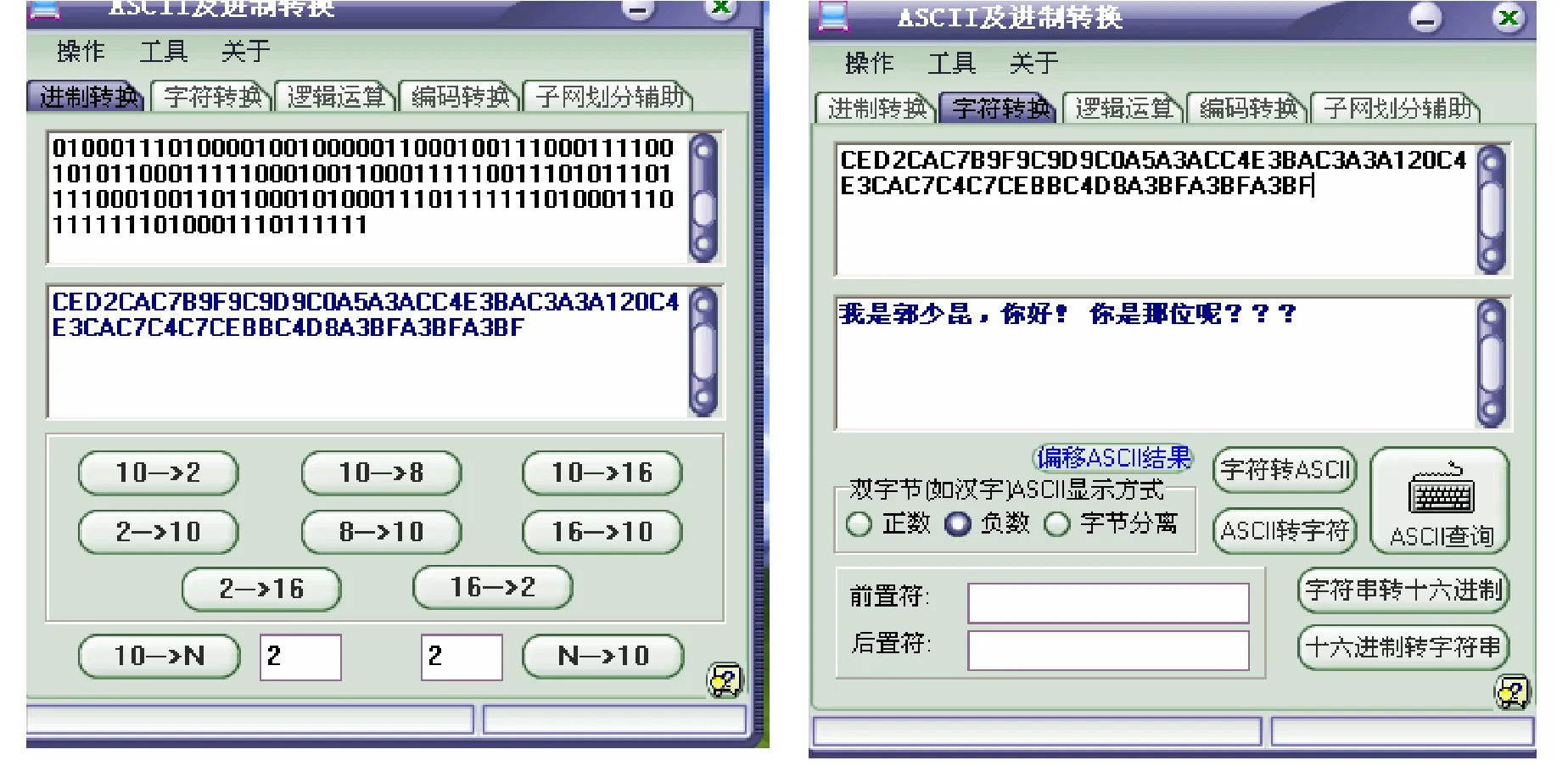
图4 数值信息转化为文本信息

（4）第四步：对嵌入信息后矩阵做任意形式的调整，如交换行列、转置等。从而打乱原有文本信息的秩序，达到加密的目的。

（5）第五步：用idwt函数对含有文本信息的图像进行重构。

信息提取是将含有文本信息的图像进行小波分解变换，分离出相应得文本信息，通过解密程序以及 fopen，fprint函数写成纯数值文本，借助turn5工具转化为文字文本。

具体解密步骤如下：

（1） 第一步：用dwt2函数对含有文本信息的图像进行小波分解，分离出含有文本信息的高频系数，以便对文本信息的读取。

（2）第二步：用相应程序对分离出的高频信息矩阵进行解密处理。

（3）第三步：对嵌入的二进制文本信息进行精确分离。还原原来的文本信息矩阵。

（4）第四步：用Matlab中的fopen ，fprint函数将分离出的文本信息矩阵写成只含有数值文本。

（5）第五步：借助 turu5转换工具将数值文本转化为所传输的文本。

例如图5：

图5 第一种加密方法

图5是对图3所显示的文本信息嵌入后的两图像之间的对比。原始图像是未嵌入信息的图像，嵌入文本信息图像是嵌入文本信息后要传输的图像。

详细的嵌入加密程序以及分离解密程序见附录程序1。

第二种加密方法：和第一种方法类似只是在将文本信息转化十六进制的符号文本信息后用。其优点是在传输中隐藏的信息量是第一种的四倍，在读取这个数值文本信息时用的Matlab函数是fopen和fread，而在逆转换过程中只需将fprint函数稍做调整即可。

图6 第二种方法加密

用第二种方法加密原始图像的信息具体程序见附录程序2。图6是经第二种方法加密后的图像对比。可知其较第一种加密方法的图像有些粗糙。

5 结束语

本文提出的是基于小波变换的在图像中嵌入文本加密信息的隐蔽方法，此方法的优点是（1）由于文本信息隐蔽于能量较低高频系数之中，所以在视觉效果图像几乎没有什么改变。（2）不同于水印技术的繁琐算法和阈值的选取，相对简单便于操作。（3）对于图像的选取没有什么特别的要求。不足之处是传递的信息量受图像信息量的影响，抗干扰能力不是很强。所以较适合普通互连网用户的文本隐蔽传输中的应用。

附录：

程序1

clear

%装入原图像1

load woman;

I=X;

%小波函数

type='db1';

%2维离散Daubechies小波变换

[CA1,CH1,CV1,CD1]=dwt2(I,type);

C1=[CH1 CV1 CD1];

%系数矩阵大小

[length1,width1]=size(CA1);

[M1,N1]=size(C1);

%图像中加入文本信息

fid=fopen('shaokun.txt');

A=fscanf(fid,'%1d');

N=length(A);

k=1;

for counter1=1:1:M1

for counter2=1:1:N1

if (k

marked1(counter1,counter2)=A(k);

else

marked1(counter1,counter2)=0;

end

k=k+1;

end

end

%重构图像

NEWCH1= marked1(1:length1,1:width1);

NEWCV1= marked1(1:length1,width1+1:2*width1);

NEWCD1= marked1(1:length1,2*width1+1:3*width1);

Rl=double(idwt2(CA1,NEWCH1,NEWCV1,NEWCD1,type));

%两图像之间的差异显示

watermark1=double(Rl)-double(I);

figure(1);

subplot(1,2,1)

image(I);

axis('square');

title('原始图像');

subplot(1,2,2);

imshow(Rl/250);

axis('square');

title('嵌入文本信息后的图像');

figure(3);

imshow(watermark1*10^16);

axis('square');

title('差异图');

fclose(fid);

% ------------解密过程-------------

[a,b,c,d]=dwt2(Rl,type);

e=floor([b,c,d]);

[m,n]=size(e);

s=1;

for i=1:m

for j=1:n

if(s

g(s)=e(i,j);

s=s+1;

end

end

end

fid2=fopen('juzhen.txt','wb');

count=fprintf(fid2,'%1d',g);

fclose(fid2);

程序2

clear

%装入原图像1

load woman;

I=X;

%小波函数

type='db1';

%2维离散Daubechies小波变换

[CA1,CH1,CV1,CD1]=dwt2(I,type);

C1=[CH1 CV1 CD1];

%系数矩阵大小

[length1,width1]=size(CA1);

[M1,N1]=size(C1);

%图像中加入水印

fid=fopen('shaokun.txt');

A=fread(fid);

N=length(A);

k=1;

for counter1=1:1:M1

for counter2=1:1:N1

if (A(k)≠N)

marked1(counter1,counter2)=A(k)

else

marked1(counter1,counter2)=0;

end

k=k+1;

end

end

%重构图像

NEWCH1= marked1(1:length1,1:width1);

NEWCV1= marked1(1:length1,width1+1:2*width1);

NEWCD1= marked1(1:length1,2*width1+1:3*width1);

Rl=double(idwt2(CA1,NEWCH1,NEWCV1,NEWCD1,type));

%分离水印

watermark1=double(Rl)-double(I);

figure(1);

subplot(1,2,1);

image(I);

axis('square');

title('原始图像');

subplot(1,2,2);

imshow(Rl/250);

axis('square');

title('嵌入文本信息后的图像');

figure(2);

imshow(watermark1*10^16);

axis('square');

title('差异图');

fclose(fid);

[1]孙崟培，王朝英.小波分析和小波包在图像消噪中的应用[J].通信技术，2009，(1).

[2]田苗苗.小波分析和小波包在图像压缩中的应用[J].安徽科技学院学报，2009，23(5).

[3]吕金花.基于MATLAB的图像压缩技术研究[J].山西焦煤科技，2008，(12).

[4]范秋凤，翟亚芳，周伟东.基于小波和小波包图像去噪的比较研究[J].信息技术，2007，(11).

[5]C.Sidney Burrus, Ramesh A.Gopinath.Introduction to wavelets and wavelet transforms: a primer(英文版)[M].北京：机械工业出版社，2005.

[6]原培新，孙丽娜，林杰，袁圣浩.基于小波变换的引擎故障诊断方法研究[J].机械科学与技术，2006.

[7]郭晶，孙伟娟.小波分析理论与MATLAB7实现[M].北京：电子工业出版社，2005.

[8]胡昌华，张军波，夏军，张伟.基于MATLAB的系统分析与设计——小波分析[M].西安：西安电子科技大学出版社，2000.

[9]戴军.一种基于小波变换和RC6的信息隐藏算法[J].信息安全与通信保密，2006，(10).