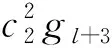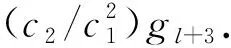关于一类极大代数上线性系统的3维最小实现的注
张 静,王 煜
(通化师范学院 数学系,吉林 通化 134002)
1 引言
设R是所有实数的集合,ε-∞,e在上定义加法⊕与乘法,如:a⊕b=max{a,b},a·b=a+b,∀其中+是一般意义下的加法,乘号·通常省略,令⊕,·},则D称为一个极大代数.
g0,g1,g2,…,gi,….
(1)
求极大代数上一个线性系统(A,B,C),即

(2)
使得
g0=CB,g1=CAB,…,gi=CAiB,….
(2)称为(1)的一个实现,(1)称为可实现序列,若(2)的维数均小于或等于(1)中任意一个实现的维数,则(2)称为(1)的最小实现,且A的阶数称为最小实现的维数.
实现理论是传统的线性系统理论的一个重要组成部分,而极大代数上线性系统的最小实现问题既是一个难题,也是一个国际上公开的问题.陈文德[2]研究了准域上的实现理论,极大代数是一类特殊的准域,但未研究最小实现问题.荷兰教授G.J.Olsder等人[3]首先提出并研究了极大代数上线性系统的最小实现问题. 随后许多学者对该问题做了研究并取得了一系列成果.2006年,文[4]对极大代数上2维最小实现问题做了研究,完全解决了2维最小实现问题.2007年,文[5]研究了几类3-阶周期序列的3维最小实现问题.得到了大部分3-阶周期序列存在3维最小实现的充要条件.
2 预备知识
定义1[6]设A为极大代数上n×n矩阵,对于λ≠ε,若存在向量X,使得AX=λX,则称λ为A的一个特征值,X称为特征向量,A的特征方程定义为:

其中系数cn-k的图论定义如下:
设矩阵A对应的有向图为G(A),在图G(A)中由一个或几个回路组成的总长度为k的回路集合,且回路集合的结点数和弧数相同,则称这个回路集合为k阶回路集.若k阶回路集中所含回路的个数为偶数ei(i∈0∪N,其中N为自然数),则记回路集的权重为W(ei,k);若k阶回路集中所含回路的个数为奇数oi(i∈0∪N),则记回路集的权重为W(oi,k).对于∀v∈R,记
Ne=‖{i;W(ei,k)=v}‖,
N0=‖{i;W(oi,k)=v}‖,


(1)gk+3=c2gk+2⊕c1gk+1,k=0,1,2,…;
(2)c0g0=c2g2,gk+3=c2gk+2⊕c1gk+1,k=1,2,3,…,且a≤c0/c1,g1>ag0,c1g1≤g3 (3)c0g0=c2g2,gk+3=c2gk+2⊕c1gk+1,k=1,2,3,…,且a≤c0/c1,g1=ag0,g3≥c0/c2⊗g1; (4)c1gk+1=c0gk,k=0,1,2,…,l,gm+3=c2gm+2⊕c1gm+1,m=l+1,l+2,l+3,…且c1gl+2≥c0gl+1,gl+3≥c2gl+2; (5)c0g0=c1g1,gk+3=c2gk+2⊕c1gk+1,k=1,2,3,…,且c0/c1⊗g1≤g2 其中l为奇数时, l为偶数时, 则 当l为奇数时: 其中由gl+3≥c2gl+2得(c2/c1)gl+2≤(1/c1)gl+3.又由gl+3⊕c0gl=c2gl+2⊕c1gl+1及c1gl+1=c0gl知gl+3≤c1gl+1即gl+1≥(1/c1)gl+3,否则与gl+1的取法矛盾. 其中由c2gl+2≥c0gl+1得gl+2≥(c0/c1)gl+1. 其中gl+3≥c2gl+2>(c0/c1)gl+2≥(c0/c1)2gl+1. 而gl+5=c2gl+4⊕c1gl+3=c2(c1gl+2⊕c2gl+3)⊕ c1c2gl+2⊕c1gl+3 从而CAl+5B=gl+5. m=2k,k≥2, 一般地 同样地可以证明l为偶数的情况. 参考文献: [1]孙志敏.极大代数上线性系统的最小实现与最优调度[D].北京:中国科学院研究生院,2006. [2]陈文德.准域上系统的能达能观性与实现理论[J].系统科学与数学,1986,6(2):81-89. [3]Olsder G J,De Vries R E.On an analogy of minimal realization in conventional and discrete event dynamic systems[J]. Lecture Notes in Control and Information Sciences,1988,103:149-161. [4]孙志敏,陈文德,于洪年.极大代数上线性系统的最小实现[J].控制与决策,2006,21(5):521-526. [5]孙志敏,陈文德.极大代数上线性系统的3维最小实现[J].系统科学与数学,2007,27(4):499-509. [6]Blondel V. D.,Portier N.,The minimal realization problem in the max-plus semiring and pisot' s problem are NP-hard [J].C.R.Acad.Sci.Paris ,t,333,SerieI,2001:1127-1130.3 一类无穷序列的3维最小实现的另一种形式