强诣零Armendariz环

崔书英

（山东工商学院 数学与信息科学学院，山东 烟台 264005）

1 引言

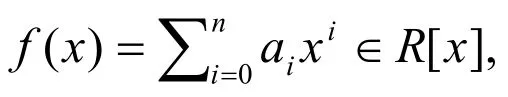
2 强诣零Armendariz环

定义1环R称为强诣零Armendariz的如果对于任意的 f (x),g(x) ∈ R[x]，当 f( x)g(x)∈ Nil*(R )[x]时有ab∈ Nil*(R)，其中a,b分别是 f (x),g(x)的任何系数。

定理1 R是强诣零Armendariz环当且仅当 R/Nil*(R)是Armendariz环。

命题1 令R是环而I是R的理想满足 I⊆ Nil*(R)，那么R是强诣零Armendariz环当且仅当R/I是强诣零Armendariz环。

证明 注意到R/I的素理想恰具形式P/I，其中P是R的包含I的素理想，所以当 I⊆ Nil*(R)时有，Nil*(R /I)=Nil*(R)/I 。由此仿照定理1的证明可证明命题1。

仿定理1的证明我们还可对诣零Armendariz环作出一个新的刻画。

定理2 环R是诣零Armendariz的当且仅当对于任意的 f (x),g(x)∈ R[x ],如果 f (x)g(x)∈ Nil*(R )[x]，那么ab∈ Nil*(R)，其中a,b分别是 f (x),g(x)的任何系数。

证明 文献[1](3128-3140)定理3.5证明了环R是诣零Armendariz的当且仅当 R /Nil*(R)是Armendariz的。基于此事实，仿定理1的证明不难证明定理2。

由文献[1]中的结果知Armendariz环是诣零Armendariz的。然而并不能明显看出强诣零Armendariz环也是诣零Armendariz的，为证明这一论断的正确性我们需要下面的命题。

命题2 如果R是强诣零Armendariz环，那么 Nil (R)= Nil*(R)。*

证明 我们断言如果a∈R满足 a2∈ Nil(R)那么 aN (R)a ⊆ Nil (R)。事实上对任意的 b∈ N(R),存在正**整数k≥2使得bk=0。由于

所以 aba∈ Nil*(R),从而断言成立。如果 Nil*(R)≠ Nil*(R),那么存在 a∈ Nil*(R)，但是 a∉ Nil*(R)。因为a是幂零元所以存在最小的正整数k使得 ak∉ Nil*(R),但 ak+1∈ Nil*(R)。令b=ak,则 b∉ Nil*(R)，但是b2∈ Nil*(R)。由证明过的断言可以知道 bN (R)b ⊆ Nil*(R)。由 b∈ Nil*(R)知 RbR⊆ Nil*(R),于是有bRbRb⊆ Nil(R)。从而可以得到 (RbR )3=RbRbRbR ⊆Nil(R)。因为 Nil (R)是R的半素理想，所以***RbR⊆ Nil*(R)。由此可知 b∈ Nil*(R),这是一个矛盾。命题得证。

由定理1，命题2和[1]定理3.5可得到下面的推论。

推论1 如果环R为强诣零Armendariz的，那么它为诣零Armendariz的。

由强诣零Armendariz的定义下列两个命题都不是容易看出的。

命题3 Armendariz环是强诣零Armendariz环。

证明 设R是Armendariz环。由文献[4]引理2.3知 Nil (R)= Nil*(R),而由文献[1]又知R是诣零Armendariz*环，所以[1]定理3.5蕴含 R/Nil*(R)是Armendariz环，再由命题1知R是强诣零Armendariz环。

由于约化环是Armendariz的[5]14-17，定理1蕴含2-素环是强诣零Armendariz的。因此定理1和命题3蕴含强诣零Armendariz环是2-素环和Armendariz环的共同推广。

定理3 环R是强诣零Armendariz的当且仅当其每个子环S是强诣零Armendariz的。

证明 设R是强诣零Armendariz的，那么 R/Nil*(R)是Armendariz的。从而其子环 (S+Nil*(R)/Nil*(R)也是Armendariz的。由于 S/S ∩ Nil*(R)≅S+ Nil*(R)/Nil*(R),所以 S /S ∩ Nil*(R)是Armendariz的。我们断言 S∩Nil*(R)⊆Nil*(S )。事实上，如果 a∈ S ∩ Nil*(R),那么a∈S且a是R中的强幂零元，所以R中以a为首项的任意m-序列有限步终止，因此S中以a为首项的任意m-序列也有限步终止，从而断言成立。因为S /S ∩ Nil*(R)是Armendariz的以及 S∩Nil*(R)⊆Nil*(S )，由命题1和命题3可知S是强诣零Armendariz的。充分性是明显的。

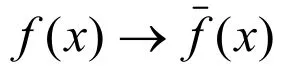
定理4 环R是强诣零Armendariz的当且仅当R[x]是强诣零Armendariz的。由此可知对强诣零Armendariz 环R有 N (R[x])= N(R)[x]。

注意到半交换环是2-素环所以是强诣零Armendariz环而诣零Armendariz环是弱Armendariz环[1]3128-3140，我们立即得到下列推论。

推论2 如果R是半交换环，那么R[x]是弱Armendariz环。[3]2607-2616

命题4 有限个强诣零Armendariz环的直积还是强诣零Armendariz的。

命题5 环R是强诣零Armendariz的当且仅当Tn(R)是强诣零Armendariz的。

推论3 环R是强诣零Armendariz的当且仅当 R[ x]/(xn)是强诣零Armendariz的其中(xn)是 xn在R[x]中生成的理想n≥2是正整数。

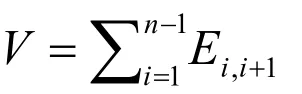
环R称为弱Armendariz的如果对任意的 f (x),g(x) ∈ R[x]当 f(x)g(x)=0时必有 ab∈ N(R)其中a,b分别是 f (x),g(x)的任何系数[3]。由文献[1]知诣零Armendariz 环是弱Armendariz 环。文献[3]定理3.6证明了如果存在R的半交换理想I,使得R/I为弱Armendariz环则R也是弱Armendariz的。该结果可推广到I是NI-环的情形，这里NI-环I是指I满足条件 Nil*(I )= Nil(I )[8]186-199，显然它是2-素环的推广。

命题6 令I是环R的理想使得R/I为弱Armendariz，如果I是NI-环则R为弱Armendariz环。

推论 4 （[4，定理 3.6]） 令I是环R的理想使得R/I为弱 Armendariz，如果I是半交换环则R为弱Armendariz环。

最后我们来给出必要的例子。

例1 存在强诣零Armendariz环但不是2-素环，存在诣零Armendariz环但非强诣零Armendariz的。前者由文献[1]例 4.8可知，因为存在非 2-素的 Armendariz环。由文献[9]定理 6.6知存在不含单位元的单诣零环I。令R= E(I,Z)是I的单位化环其中Z是整数环[7]，则有 Nil*(R)= (I ,0),Nil (R)=0[7]，由命题2知R不是强诣*零Armendariz环。但 R / Nil*(I ) ≅ Z,所以R是诣零Armendariz环。此外由文献[6]知存在素根为零的不含单位元的局部幂零环I。令 R= E(I,Z)则容易证明R是诣零Armendariz环。但它不是强诣零Armendariz环，否则将有 0=Nil (I,0)=Nil(R)=Nil*(R),这与 Nil*(R)=(I ,0)≠0相矛盾。**

[1]R. Antoine. Nilpotent elements and Armendariz rings[J]. J. Alg . 2008, (319): 3128-3140.

[2]D.D.Anderson,V.P.Camillo. Armendariz rings and Gaussian rings[J]. Comm. Alg., 1997, 26 (7).

[3]Z.Liu, R.Zhao. On weak Armendariz rings[J]. Comm. Alg, 2006, 34(7) :2607-2616.

[4]N.K.Kim etal.. Power series rings satisfying a zero divisor property[J]. Comm. Alg, 2006, 34(6) :2205-2218.

[5]M.B.Rege,S. Chhawchharia, Armendariz rings, Proc. Japan Acad[J]. Ser. A, Math. Sci, 1997, (73):14-17.

[6]T.Y. Lam. A First Course i n Noncommutative Rings[M] Springer-Verlag, New York ,1991.

[7]陈卫星. NCI环的多项式环未必是NCI环[J]. 辽宁师范大学学报：自然科学版，2008，30 (2),.

[8]S.U.Hwang etal.. Structure and topological conditions of NI-rings[J]. J. Alg, 2006, (302).

[9]A.Smoktunowicz. A simple nil ring exists[J]. Comm. Alg , 2002, 30(1): 27-59.