基于直接邻域保护嵌入的人脸识别

孙庆娟

（聊城大学 数学科学学院， 山东 聊城 252059）

1 引言

人脸识别是利用计算机分析人脸图像，从中提取有用的识别信息来辨别身份的一门技术。近年来，相继提出了许多种人脸识别方法，这些方法面临的一个主要问题就是图像维数太大，解决这一问题的方法就是进行维数约简，即降维。现已有许多可行的线性降维方法，包括主成分分析（PCA）[1]71-86，线性判别分析（LDA）[2]711-720等。这两种方法都只考虑了人脸图像的全局结构，而忽略了局部结构，但在许多实际的分类问题中，特别是采用最近邻方法进行分类时，局部结构比全局结构能提供更加重要的信息。NPE算法[3]208-213是一种用于人脸表示和识别的线性降维方法，它主要是对局部线性嵌入（LLE）算法[4]2323-2326的线性逼近，不但继承了LLE的优点，而且充分考虑了人脸图像的流形结构。

NPE在处理高维数据时同样面临着矩阵奇异性问题，因此本文提出一种直接算法，并在ORL人脸库上通过实验证明了该方法的有效性。

2 邻域保护嵌入(NPE)算法

NPE算法是一种用于人脸表示和识别的线性降维方法。给定一组人脸数据集{x1,… ,xn} ⊂Rm，假设X= [x1,… ,xn]，文献[3]给出的NPE 算法的具体步骤如下：

（1） 构造邻域图：设G为有n个节点的图，第i个节点与人脸图xi相对应。如果xi是xj的k近邻，或xj是 xi的k近邻，则在它们之间连上一条边。

（2） 选择权值：设N表示权值矩阵，其每条边上的权值为Nij，规定没有边连接的Nij为零。利用下面的准则函数求这些权值：

约束条件

（3） 考虑一种极限情况，将n维空间的数据投影到一条直线上，其映射为 y=(y,…,y)T。由于在这条1n直线上的每一个数据都可表示为其邻域点的线性组合，因此我们可以最小化下面的重构误差函数：

另外，假设投影是线性的，即 yT= wTX ，经过简单的代数变换，代价函数变为 Φ(y ) =wTXMXTw，其中M=(I −N)T(I −N)，I= diag(1,…,1)。为了排除尺度因子的影响，增加约束 yTy=1⇒wTXXTw =1，最终优化问题变为

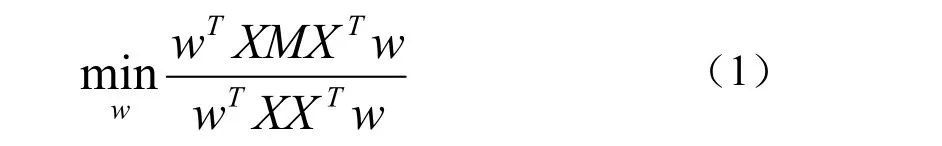
实际上这是一个关于求解下列广义特征向量的问题：

3 直接邻域保护嵌入算法（DNPE）

一般地，广义特征向量的求解还存在着一个问题，就是X的行向量可能是线性相关的，从而导致 XXT奇异。在线性代数中，求解广义特征值问题的一种常用方法是采用同时对角化的思想。由于矩阵M是对称半正定的，所以矩阵 XMXT和 XXT都是对称半正定的。该方法的主要原理是通过对角化 XXT来去掉它的零空间，再通过投影和对角化 XMXT来寻找投影向量。

引理：邻域保护嵌入方法中， XXT的零空间不包含任何判别信息。

算法试图寻找一个投影矩阵W能同时对角化 XMXT和 XXT，使得 WXXTW =I ， WXMXTWT=Λ，其中Λ是升序排列的对角矩阵。为了降低维数到d(d＜＜n)，简单挑选W的前d行，其对应Λ中最小的d个对角元素[5]。

具体步骤如下：

（1）对角化 XXT：寻找正交矩阵 V (VVT=I )，使得 VXXTVT=Λ1，其中Λ1是降序排列的对角矩阵，可以通过传统的特征值分解方法来得到，即V的每一行是 XXT的一个特征向量，Λ1包含了其所有的特征值。因为XXT可能是奇异的，所以其一些特征值可能为零（或接近于零），因此需要去掉这些特征值和特征向量（因为这些方向的投影对邻域保护嵌入来说不包含任何有用的判别信息）。

设Y∈ Rm×n（n是特征空间的维数）是V的前m行，则 YXXTYT= Di＞0，其中Di为对应于非零特征值的m×n对角矩阵。

（3） 计算投影矩阵W：令 W= U1Z，则W满足（1）式。对于一个给定的n维的输入x，它在其特征空间的投影向量为y=Wx，此时y的维数降为d（d＜＜n）。

4 实验和结果分析

为验证上述分析结果，我们对PCA，PCA+LDA，NPE和本文算法（DNPE）分别在标准ORL人脸图像库上进行了比较试验。为了结果的客观性和可比性，采用了统一的图像预处理和最近邻分类器，距离测量使用欧氏距离。ORL人脸图像库包括40个人，每个人10幅图像。在ORL库中随机抽取每人5幅图像作为训练集，其余作为测试集，并运行20次获得平均正确识别率。PCA，PCA+LDA，NPE和DNPE的平均识别率分别为85.9%，92.2%，92.7%和94.1%。

从上述结果可以看出，本文算法对高维的图像数据来说是一个较优的求解算法，取得了比其他算法更高的识别率。一方面说明考虑局部流形结构的降维方法能更有效地得到数据邻域的分布特性，同时也说明了通过同时对角化的投影变换的确能提高识别率。

5 结束语

本文提出一种新的直接邻域保护嵌入算法并将其应用于人脸识别，该算法在传统NPE算法的基础上进行了改进，与其他算法相比，取得了较高的识别率。

[1]M.Turk, A.Pentland, Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1992, (3).

[2]P.Belhumeur, J.Hespanha, D.kriegman, Eigenfaces vs. Fisherfaces: recognition using class specific linear projection[J]. IEEE Trans. Pattern Anal. Mach. Intell, 1997, (19).

[3]X.He, D.Cai, S.Yan et a1.Neighborhood Preserving Embedding[J]. IEEE International Conference on Computer Vision. 2005,(1).

[4]Roweis S T, Saul L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding[J]. Science, 2000, 290(5 500).

[5]K.Fukunaga. Introduction to Statistical Pattern Recogniton: 2nd Edition[M]. New York: Academic Press, 1990.