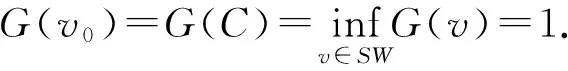Neumann边条件下薛定谔算子前两个特征值间距的估计

周 敏,向会立

(湖北民族学院 理学院,湖北 恩施 445000)

在薛定谔方程中特征值对应于系统的能量，薛定谔算子第二特征值与第一特征值的差对应于离子从第一能级跃迁到第二能级所需吸收的能量，因此在数学上求出薛定谔方程的特征值是十分有意义的事情，但一般来讲，由于数学上的原因，特征值的确切解很难求出，因此只好退而求其次，给出特征值之间间距的估计.在势函数为特殊函数情形行下对薛定谔算子前两个特征值估计见文献[1～5],对于Dirichlet边条件下薛定谔算子第二特征值与第一特征值的差文献[3]已给出了相应估计，本文讨论了Neumann边条件下薛定谔算子前两个特征值间距的估计.

定义1 称下有界函数v为区间[0,π]上的单阱函数，若v在[0,π/2]上单调递减，在[π/2,π]上单调递增.记所有单阱函数全体构成的集合为SW.

定义2 考虑S-L问题:

(1)

本文结论：S-L问题:

(2)

在SW中的最优势函数为常函数C,且有:

引理1[1]设λn(t)为S-L问题(1)的第n个特征值，un(x,t)为对应的第n个归一化特征函数，则有:

定义3 由引理4可将势函数v分成如下两类：

引理5 设u1(x)，u2(x)为：S-L问题(2)的第一，第二归一化特征函数，则:

(1)若v为第一类势函数，则存在x+，x-满足0≤x-

(2)若v为第二类势函数，则只有以下两类情况:

(i)∃x*∈(0,π)使得:

(ii)∃x*∈(0,π)使得:

引理6[1]设λ1(t)，λ2(t) 为S-L问题(2)的第一，第二特征值，则:

且:

引理7 定义AM={v:0≤v≤M,v∈SW}则AM⊂SW且AM为凸集.

证明由AM的定义AM⊂SW是显然的.下证AM为凸集.

∀v1,v2∈AM及∀t∈[0,1]有0≤tv1+(1-t)v2≤M又tv1∈SW,(1-t)v2∈SW故tv1+(1-t)v2∈SW,故tv1+(1-t)v2∈AM即AM为凸集.

定理1 设λ1(v)，λ2(v)为S-L问题.

(其中v(x)∈AM)的第一，第二特征值，G(v)=λ2(v)-λ1(v)则S-L问题(2)在AM中的最优势函数为常函数C,且有:

证明由文献[1]知，在AM中S-L问题(2)的最优势函数存在这里记为v0，下面分两种情形来确定v0的具体形式：

(1)v0为第一类势函数的情形：

由引理5知，存在x+，x-满足0≤x-

(3)

①x-≤π/2

(4)

由式(3)，(4)知上述不等式成立当且仅当v1(x)=v0(x)，从而v0(x)必为如下形式的阶梯函数：

②π/2

同情形①一样可以证明：v1(x)=v0(x).

其中0≤m1≤M,0≤m2≤M.

(2)v0为第二类势函数的情形：

此时同情形①一样，可以证明当M≥1时v0(x)必为如下形式的阶梯函数：

其中0≤n1≤M,0≤n2≤M.

综合情形①和情形②可得只要v0(x)为最优势函数则其必为如下形式的阶梯函数：

其中0≤m≤M,0≤n≤M.

(5)

下面进一步来确定v0(x)的形式，证明m=n，从而说明最优势函数v0(x)只肯能为常函数.事实上，当v0(x)为式(5)的形式时，S-L问题(2)的特征函数可表示为：

(6)

因为y(x)为S-L问题(2)的特征函数，故必须适当选取c,d的值，使得y,y'∈AC[0,π]即:

(7)

此时一方面将方程组(7)看作关于λ的方程组则其非负实解对应于S-L问题(2)的所有特征值，另一方面方程组(7)与方程:

(8)

同解，对方程(8)作变换t=λ-m得到方程:

(9)

[1]Miklos Horvath.On the first two eigenvalues of Sturm-Liouville operators[J].proceedings,2003,131(4):1 215-1 224.

[2]向会立.Sturmm-Liouville问题前两个特征值间距的估计[J].湖北民学院学学报:自然科学版,2007,25(2):148-150.

[3]Richard Lavine. The eigenvalue gap for one-dimensional convex potentials[J].Proceedings of the American mathematical Society,1994,121(3):895-902.

[4]Richard Lavine. The eigenvalues gap for one dimensional convex potentials Proceeding[J].2003,124(4):815-821.

[5]Kobayashi M. Eigenvalues of discontinuous Sturm-Liouville problems With symmetric potentials[J].Computers Math Applic,1989,18(4):357-364.

[6]周敏.一类与算子谱对应的方程解得性质研究[J].湖北民族学院学报:自然科学版,2009，27(4)：391-393.