带违约风险及转股价向下修正的可转债分析

陈 稹

(浙江工商大学,浙江杭州 310018)

带违约风险及转股价向下修正的可转债分析

陈 稹

(浙江工商大学,浙江杭州 310018)

基于转股价可向下修正的可转换债券的偏微分方程,结合违约时间的概率密度函数,得出带违约风险及转股价可向下修正的可转换债券模型;把连续时间离散化,最后实证分析得出违约风险条款弱化可转换债券的价值,而可向下修正条款趋于增加可转换债券的价值。

期权定价模型;二叉树方法;可转换债券;风险中性

一、引言

可转换债券是一种附有转股权的特殊债券,在转股之前是一种公司债券,具备债券的一切特征;在转股之后,具有股票的特性,持有人由债权人转变成了股权所有者。由于可转换债券的利率低于普通债券的利率,发行公司通过可转换债券融资可以减低其成本;同时又因其利息支付优先于派发红利的特点,投资可转换债券将比股票更有保障。近年来,随着我国金融市场的进一步完善和开放,大量的国际资本开始涌入我国证券市场,各种投资基金纷纷登陆中国这一新兴资本市场,新的投资理论开始冲击原有的一些投资策略。可转换债券以其独特的特点受到了证券市场方方面面的青睐,尤其在外资基金中,花旗集团、瑞银华宝、摩根士丹利等合格境外机构投资者都持有大量的可转换债券。上市公司为了满足经济高速发展的需要和扩大规模的欲望,也纷纷发行可转换债券来融资。

前人对可转换债券定价的研究大致可以分为两大类:基于公司价值的定价模型和基于权益价值的定价模型。

基于公司价值的可转换债券的定价模型最早见于 Ingersoll(1977)[1]、Brennan和 Schwartz(1977)[2],他们假设公司价值服从几何 Brown运动,可转换债券的价值依赖于公司价值

这一标的变量,运用Black—Scholes的期权定价方法导出了可转换债券的价值。但是该模型假设利率为常数,但可转换债券的期限一般都很长,假设利率为常数就显得不尽合理。后来 Brennan和Schwartz(1980)[3]考虑了利率的波动,认为可转换债券受公司价值和市场利率波动因素的影响,导出了可转换债券所满足的偏微分方程,利用数值方法给出了模型的解。Nyborg(1996)[4]在 Brennan等人的模型基础上考虑了回售条款和浮动利息对可转换债券价值的影响。但是由于公司价值的相关数据在实际中很难获得,因而减弱了其研究价值。

基于权益价值的可转换债券的定价模型首先由Mc Connel和 Schwartz(1986)[5]建立,模型假设公司的股票价格服从波动率为常数的几何 Brown运动,用Black—Scholes的期权定价理论导出了可转换债券满足的偏微分方程,求出了其理论价值,但模型没有考虑公司的违约风险对可转换债券价值的影响。后来 Goldman Sachs(1994)[6]将违约风险因素考虑进了可转换债券的定价模型中,并假设利率、股票波动率和违约风险率都是已知的常数,可转换债券的价值只依赖于公司股票的不确定性,导出了可转换债券满足的偏微分方程。Tsiveritotis和 Fernandes (1998)[7]进一步将股价的单因素定价模型进行完善,把可转换债券的价值分解为现金部分和权益部分,其中现金部分采用风险折现率折现,权益部分采用无风险利率折现。

虽然 Goldman Sachs也研究过考虑违约风险的可转换债券,但是本文将可转换债券隐含期权视为一种奇异期权,而不是欧式期权。本文基于转股价可向下修正的可转换债券的偏微分方程,结合违约时间的概率密度函数得出带违约风险及转股价可向下修正的可转换债券模型;把连续时间离散化,最后实证分析各个条款对可转换债券的价值影响。

二、模型建立

在建立模型之前先做一些基本假设:

①股票价格 St服从几何 Brown运动 dSt=rStdt +σStdWt,其中 dWt为 W iener过程,r为无风险利率,σ为瞬时波动率。

②若可转换债券到期前ω天的最高价 J低于αS0,转股价向下修正为βS0(0<α,β<1)为常数。其中 S0为初始转股价,可转换债券的票面利率为r0。

③市场是完备的且不存在无风险套利机会。

X表示可转换债券在 T时的转股价,由假设②知:

在到期 T时刻,转股的最优策略是最大化转成股票后的价值与继续持有债券的价值,得到:

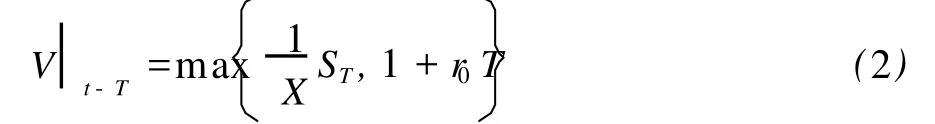
由 Ito引理和Δ-对冲原理得到可转换债券价值V=V(S,J,t)适合以下偏微分方程:

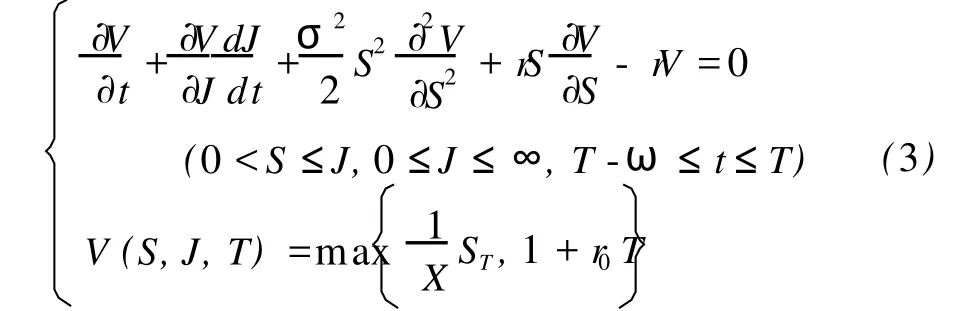
由于式(3)模型中最大股价 J不是 t的可微函数,对 J进行逼近。

令

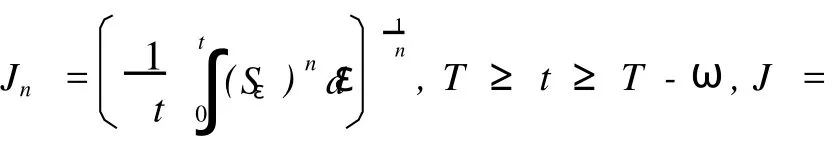
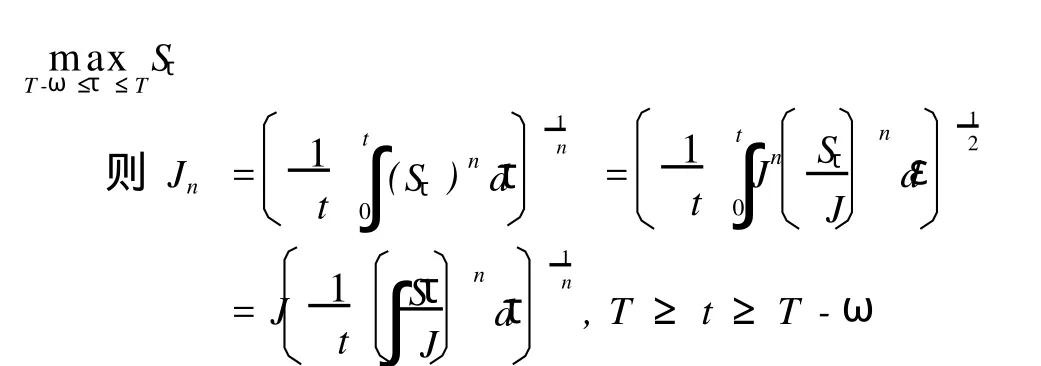
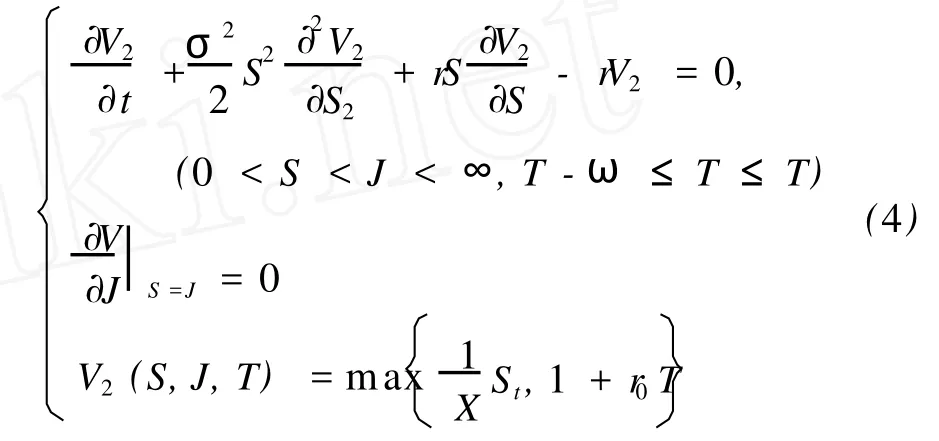
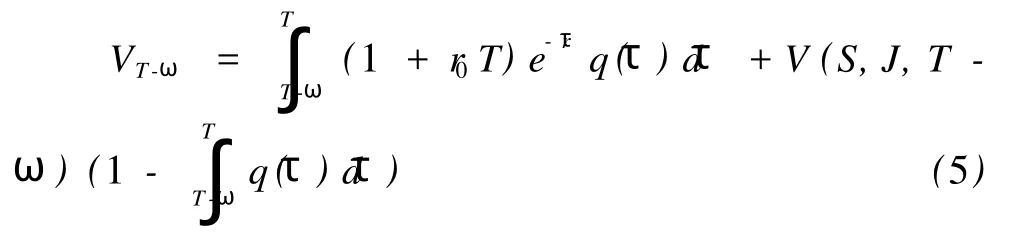
在风险中性情况下,发行日可转换债券的价格:

假定违约时间概率密度函数为 q(τ),τ为违约时间。如在期权生存期发行商没有发生违约即τ> T,可转换债券的价格为 V=V(S,J,t),如果在期权生存期发生了违约即 T-ω≤τ≤T,期权被迫自动终止,可转换债券的持有人只能向发行商索赔金额 1 +r0T。可转换债券的价值就是依赖于违约时间的合约价格的数学期望。有

三、各条款对可转换债券价值的实证分析

为了评估各条款对可转换债券价值的影响,本文把连续时间离散化,建立以上模型相适应的二叉树模型。对模型的参数设置如下:无风险利率为 r= 2%,可转换债券挂钩的标的股票的价格为 S=6.86;波动率为σ=0.4;可转债券的票面利率 r0=1.5%,面值为 100,到期期限为 2年,转股价的参考标准为债券到期前的半年如股价的最高价低于初始转股价(X=10)的 90%时,转股价向下修正 80%,且只能在到期实施转股;假定违约时间密度函数服从λ=0.5的指数分布。利用SAS软件编程得到发行时的价值,结果如表 1所示。

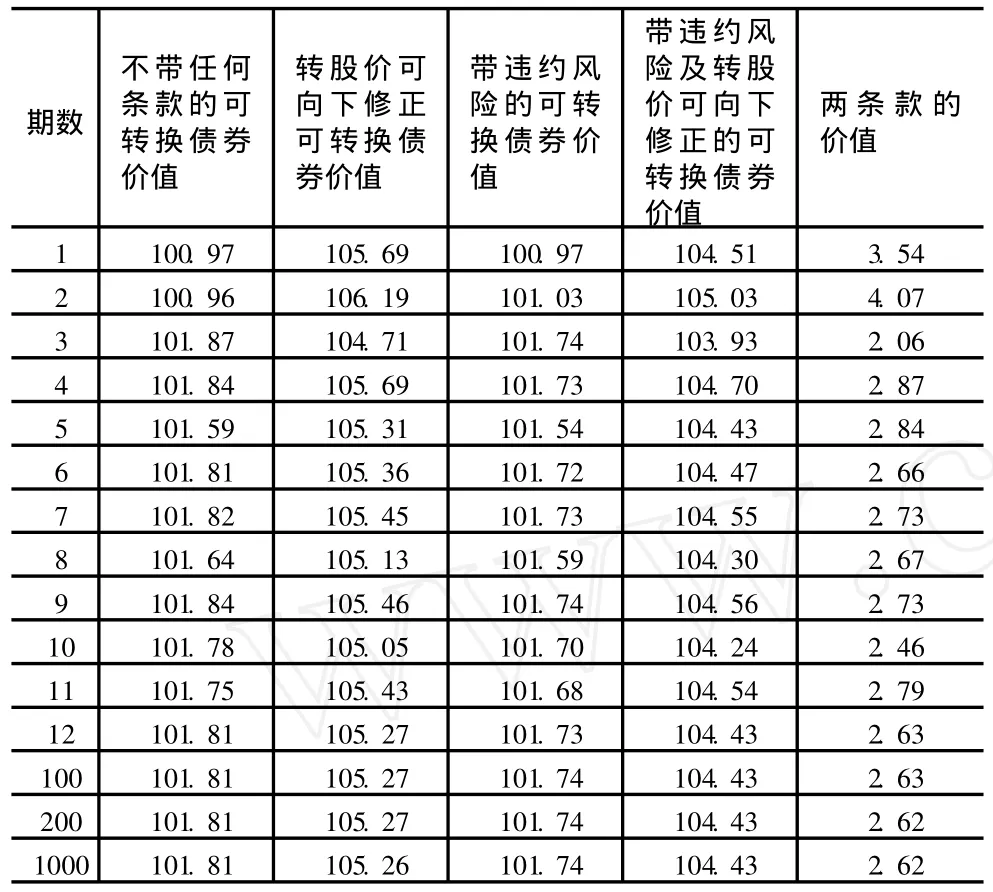
表1 不同条款合约的可转换债券价值

由表 1可知,向下修正条款趋向于增加可转换债券的价值,而违约风险条款弱化可转换债券的价值;带违约风险及转股价可向下修正的可转换债券价值落于转股价可向下修正可转换债券价与带违约风险的可转换债券价值之间;由于二叉树的极限收敛于模型 (4),因此随着二叉树模型期数不断增多,表中各列的价值都趋于收敛。

四、结束语

精确的评价风险投资项目的价值在风险投资项目研究中,特别是在金融大风暴、投资热情极度缺乏、企业融资困难的前提下具有非常重要的意义。本文通过将连续的时间离散化,在合理的假定下,得到了可转换债券的二叉树定价模型的数值解,并通过 SAS编程分析出了两种条款对可转换债券价值的影响,进而为投资者的投资决策建立了数理分析基础。同样的分析也适用于其他金融衍生产品的定价。

[1]J.Ingersoll. A Contingent-claim’s Valuation of Convertible Securities[J].1997,(4):289-322.

[2]Brennan M.J.and Schwartz E.Convertible Bonds: Valuation and Optimal Strategies for Call and Conversion[J]. 1977:1699-1715.

[3]BrennanM.J.and Schwartz E.Analyzing Convertible Bonds[J].1980,(2):907-929.

[4]Nyborg K.The Use and Pricing of Convertible Bonds. Applied[J].1996,(3):167-190.

[5]Mc Connell J J and Schwartz E S.LYON Taming[J]. 1986,(4):561-576.

[6] Goldman Sachs.ValuingConvertibleBondsas Derivatives[A].11.1994.1-30.

[7]Tsiveriotis K.and Fernandes C.Valuing Convertible Bondswith Credit Risk[J].1998,(8):95-102.

[8]Merton R.On the pricing of corporate debt:the risk structure of interest rates[M].1995.6-12.

[9]Black F.and J.C.Cox,Valuing corporate securities. Some effects of bond indenture provisions[J].1976,31:351-367.

[10]姜礼尚.金融衍生产品定价的数学模型与案例分析(第三版)[M].北京:高等教育出版社.2003.212-222.

F830

A

1008-2670(2010)05-0028-02

2010-09-08

本文系浙江工商大学研究生科研基金项目(1020XJ1509118)。

陈稹,男,江西吉安人,浙江工商大学统计与数学学院硕士研究生,研究方向:金融工程。

(责任编辑:时明芝)