定向井有杆抽油泵系统诊断模型的建立

王 凯

(西安理工大学机械及精密仪器学院,陕西西安 710048)

定向井有杆抽油泵系统诊断模型的建立

王 凯

(西安理工大学机械及精密仪器学院,陕西西安 710048)

考虑井眼轨迹的井斜角、方位角、油液等对杆柱抽汲运动的影响,从定向井的多级混合杆抽油杆柱上选取微元体,对该微元体做动力学分析。建立反映抽油杆柱动态变化的波动方程,作为有杆抽油泵系统故障诊断的初始动力学模型。对整个杆柱采用变步长取样和多级杆柱的分界面处特殊处理,利用有限差分法求解偏微分方程,得到杆柱上分界面处和均质段任意位置处的位移表达式。确定初始条件和边界条件,经差分和迭代计算获得抽油泵柱塞位移表达式和载荷表达式,完成最终的建模。以油田提供的 4口油井的相关数据为例,代入诊断模型得到了泵功图并对其进行故障诊断。结果表明:定向井有杆抽油泵系统诊断模型的建模方法是正确可行的,数学模型应用可靠,能够支持基于知识和基于数据分析的故障诊断方法。

建模分析;抽油杆柱;波动方程;泵功图;故障诊断

研究有杆抽油系统故障诊断离不开抽油泵示功图(简称泵功图)。泵功图可以准确地反映出井下抽油泵的实际工况,其不同形状特征代表了不同的工况。实测法获取泵功图是利用井下动力仪随同抽油泵一起下入井内直接测量泵功图[1],由于必须将抽油泵和抽油杆提出以安装井下动力仪,不能实时观察井下工况,耗资巨大且工艺复杂,没有得到推广应用[1]。刘磊明等[2-3]考虑杆柱的径向、轴向振动以及与油管液柱间的径向耦合振动完成了建模;王昱[4]将忽略了很多因素简化推导的吉布思方程采用傅里叶级数展开和分离变量法求解获得简略的诊断模型;蔡道钢[5]和王济新[6]采用显式有限差分法求解吉布思方程来获取诊断模型;李子丰等[7]对杆柱进行力学和运动分析,建立了几何方程、运动平衡方程和本构方程;梁若筠[8]从空间曲杆受力和力矩平衡原理出发,建立了定向井有杆抽油系统诊断力学模型;宋开利[9]指出采用API方法和吉布思方法建立的有杆抽油系统预测、诊断模型均适用于直井,且没有考虑液柱对抽油系统的影响。实际工程中我国大多数油井的抽油泵工作在很深的定向井中且高速运转,抽油杆柱为多级混合杆(各级杆径、材质不尽相同),油液对抽油杆柱的浮力影响不容忽视,由于存在井眼井斜角和方位角的影响,使得对这类油井的故障诊断难度增加。为取得真实可靠的诊断结果,有必要结合定向井的实际情况重新建立适用于直井和定向井的通用数学模型。

1 抽油杆柱的受力分析

为了真实地描述抽油杆柱在油管内上下往复运动过程中的变形状态,既要考虑几何非线性效应和接触非线性效应,也要考虑在运动过程中的各种摩擦阻力及惯性力等动力学效应[6]。建立抽油系统井下故障诊断数学模型的关键是建立抽油杆柱的轴向振动的波动方程,为此取抽油杆柱微元体为研究对象。如图 1所示的多级抽油杆柱 (假设级数为K),以悬点位置为原点,沿抽油杆柱轴心线向下x方向为正方向。

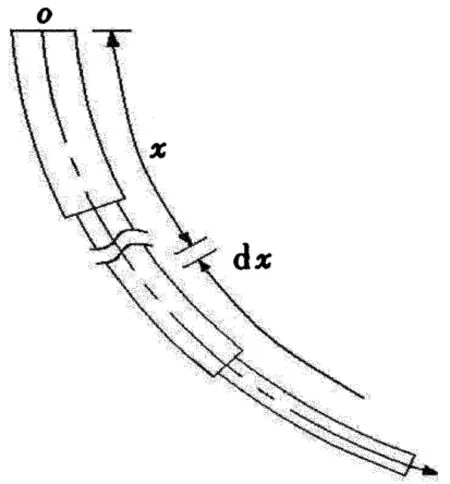
图1 多级抽油杆柱示意图Fig.1 Sketch map of multistage sucker rod string

为方便分析,约定:Ark为抽油杆柱截面积,m2;Erk为抽油杆柱的弹性模量,N/m2;g为重力加速度,m/s2;ρrk为抽油杆柱在空气中的密度,kg/m3;ρf为油液密度,kg/m3;ρ′rk为微元体在油液中的相对密度,kg/m3,且ρ′rk=ρrk-ρf;υek为单位长度上杆柱的黏滞阻尼系数,kg/(s·m);μk为第k级抽油杆柱与油管间的摩擦系数;α为井眼井斜角,(°);φ为井眼方位角, (°);q′rk为单位长度微元体在油液中的浮重,kN;δ为符号函数,上、下冲程时分别取为-1和+1。

设u(x,t)为抽油杆柱上任意位置x处的截面在任意t时刻沿井深方向的位移,建立自然坐标系和笛卡尔坐标系,微元体受力情况如图 2所示。

图2 抽油杆柱微元体受力示意图Fig.2 Sketch map of force summ ing sucker rod string infin ites imal

在抽油杆柱任意x处,抽油杆柱受以下8种力作用:

(1)抽油杆柱微元体自重Wr,Wr=ρrkgArkΔxk;

(2)抽油杆柱微元体在油液中浮力Wrf,Wrf=ρfgArkΔxk;

(3)油管对微元体的支反力(即杆管环空液体对抽油杆柱的液体静压力)N(x),

由牛顿第二定律可列出微元体所受的轴向力平衡条件∑F(x)=0,可得

由于存在井斜角,抽油杆柱在井下呈弯曲状态。油管对杆柱横向位移的约束作用以及井液对杆柱的充分润滑使得杆柱的横向位移可以忽略从而忽略油管对杆柱的刚性摩擦力frt。这样上式简化为

将上式中各项表达式代入整理,得到多级杆柱运动的波动方程为

公式(1)即为有杆抽油泵系统的故障诊断所用的力学模型的初始形式,它是一个反映抽油杆柱动态变化的二阶线性带阻尼偏微分方程。如果是直井(井眼井斜角α为 0)并忽略杆柱在油液中的浮力影响,公式(1)就转化为文献[1]中吉布思方程的形式。

相邻两级杆柱的分界面(变截面处)应满足以下连续条件:

通过载荷传感器和位移传感器在地面测得一个周期内不同时刻光杆载荷和位移的变化关系的二维封闭曲线,称作地面光杆示功图,简称地面示功图。有杆抽油泵系统的预测模型与诊断模型在初始形式上是一致的,区别只是边界条件不同,诊断模型的边界条件由地面示功图给出。对有杆抽油泵系统的预测研究和诊断研究出发点和落脚点相反,诊断研究是已知地面工况探究井下抽油泵处工况,从而得出真实的抽油泵系统的采油工况。井下抽油泵柱塞动载荷和柱塞位移的关系图即为泵功图,表现为一个周期性的封闭曲线。获取泵功图,就要推导出位于抽油杆柱末端泵处柱塞的位移表达式和动载荷表达式。

对特发性炎性肠病患者予以跨理论模型联合动机性访谈干预能够有效提高其自我效能感，动机性访谈与跨理论模型干预有效结合，其是以跨理论模型作为框架，并将对患者的健康教育分为意图转变时期、行为落实时期，其中，在意图转变时期患者已经认识到不良的生活习惯、不遵医行为会再次诱发加重特发性炎性肠病，但出于进退两难，此时给予动机性访谈为主，以此挖掘患者的行为改变动机，不断增强患者的自我管理能力意识，在行为落实时期的主要内容是建立互帮互助小组或成立特发性炎性肠病病友会，以此确保健康教育的实施连续性，对增强患者的自我效能感方面具有积极肯定的价值[14-15]。

2 抽油泵柱塞位移和动载荷求解方法

在抽油杆柱的均质杆段(等截面段),将抽油杆柱轴线离散成等步长的m个单元,步长为Δs,各单元以下标i表示,i=0,1,2,…,m,将时间t离散成n个时间段,时间步长为Δt,各时间点以下标j表示,j =0,1,2,…,n,则ui,j表示抽油杆柱上第i个节点在时刻j的位移。根据牛顿前插分公式有

将式(2)～(4)代入式(1)整理得抽油杆柱均质段位移方程为

R.W.亨别克[1]指出,式 (5)有限差分解ui,j项的系数如果为负,则其解是不稳定的,因此有限差分解的收敛条件为 2-2κ≥0,即

对于不同材料及杆径的相邻两级杆柱分界处(变截面处)的波动方程要特别对待。杆柱分界面示意图如图3所示。

图3 杆柱分界面示意图Fig.3 Sketch map of interface of rod string

设Erk,ρrk,Ark分别为第k级杆柱的弹性模量、密度与横截面积,Er(k+1),ρr(k+1),Ar(k+1)分别为第k+1级杆柱的弹性模量、密度与横截面积,则第k级杆柱、第k+1级杆柱的波动方程分别为

由杆柱变形协调及连续性条件可知两级杆柱分界面i处应满足如下条件:

将式(17),(18)分别代入公式(15),(16)并结合公式(8)得抽油杆柱分界面处诊断模型为

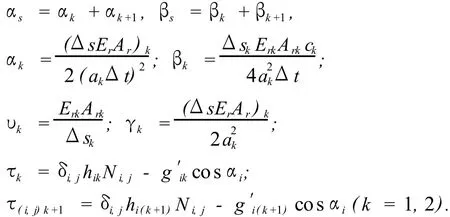
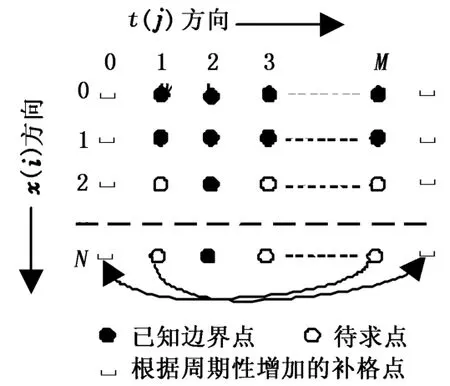
图4 波动方程计算差分网格图Fig.4 D ifference grid to wave equation calculation

图5 有限差分格式Fig.5 Fin ite difference format

如前所述,边界条件由地面示功图给出,图 4中第一行已知的M个点位移、载荷就是地面示功图上一个周期内按等时间间隔很容易采集到的M个点的位移和载荷。地面示功图中各点载荷记为F1,F2,…,FM,位移记为u1,u2,…,uM,位移方向向上为正,而杆柱位移方向向下为正,即u0,1=-u1,u0,2=-u2,…,u0,M=-uM,对应于差分网格图的第 1行(i=0)各点,成为诊断模型的有限差分方程的一个边界条件。

抽油杆柱任意节点i处在任意j时刻的动载荷

表达式为

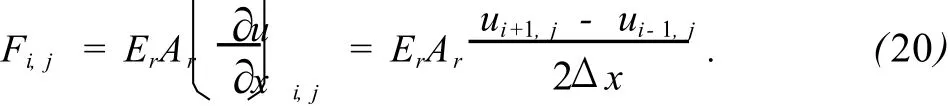
式(20)中i=0时的载荷即为沿杆柱方向零刻度处的光杆载荷,即地面示功图所表示的各点载荷,记为

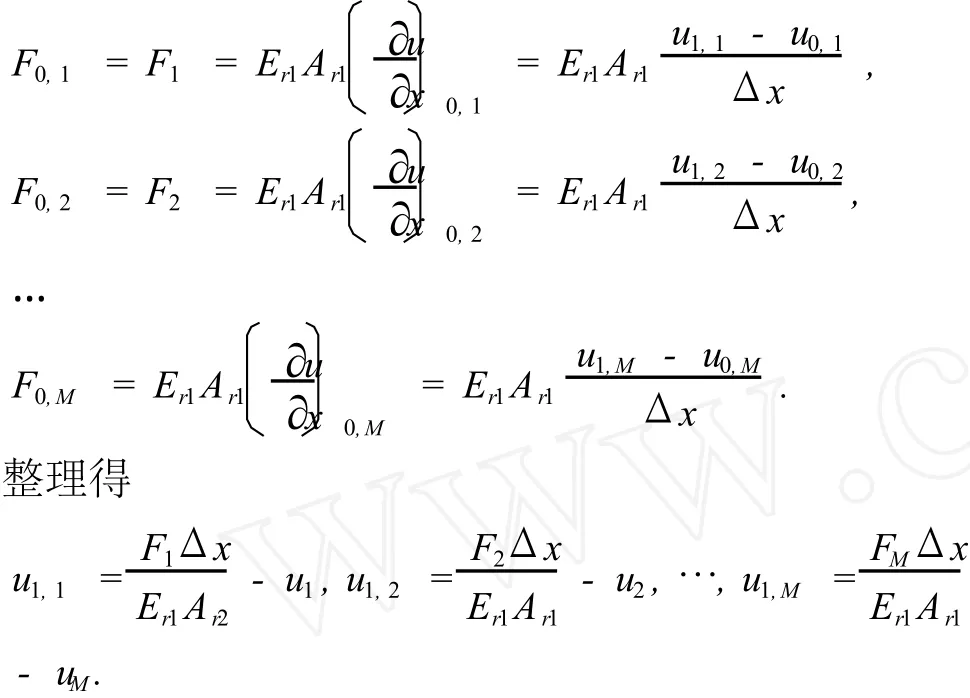
u1,1,u1,2,…,u1,M对应差分网格图的第 2行(i=1)各点,成为诊断模型的有限差分方程的另一个边界条件。

计算抽油泵柱塞位移时,从第3行(i=2)开始到最后一行(i=N)结束,逐行进行,利用诊断模型的有限差分解位移公式(5)及(19)首先计算出u2,1,u2,2,…,u2,M;接着计算u3,1,u3,2,…,u3,M;…;最后计算uN,1,uN,2,…,uN,M。

3 杆柱的末端(泵处)动载荷的计算

抽油泵处柱塞动载荷对应于抽油杆柱的末端,处于均质段。对于杆柱末端位移,由牛顿后插公式得

将式(22)和式(24)代入式(21),整理后得

可以看出,对杆柱方向上整个杆柱Δx的划分是采用变步长的方法,但是在某一级杆柱均质段采用的是等步长划分,使得该级杆柱最后一个节点位于相邻两级杆柱分界面处,以保证分界面处两端的步长仍然在两级杆柱各自的均质段内而不会跨进两级材质、杆径不同的杆柱段。

4 应用实例

西北某油田的抽油机光杆处安装的位移传感器、载荷传感器在一个抽汲周期内按照等时间间隔原则可采集到 144个点,随机选取西北某油田提供的路 45-19、西 23-26、西 31-31、西 29-29等 4口油井的光杆位移和载荷的实测数据、抽汲参数、井况数据,逐点连接成封闭的关于位移 -载荷的二维曲线,获取实测的地面示功图。将前述的建模方法编制了Matlab应用程序,经过有限差分计算和迭代计算可以得到一个周期内每口油井的抽油泵柱塞位移和载荷,并在Matlab中逐点连接成封闭的关于柱塞位移 -柱塞载荷的二维曲线,即井下泵功图,可以用于故障诊断、运行分析与模式识别等工作。将每口油井的地面示功图和泵功图共同绘制在一个坐标系内,见图6。

4口油井的泵功图分别代表了正常、液击、严重液击、轻度液击等工况。与典型工况模版库资料和油田提供的设备运行记录对比,结论正确。每口油井的地面示功图与泵功图形状相似但有区别,而这在位移轴上相差一个超行程,地面光杆载荷大于井下抽油泵柱塞载荷,泵功图在地面示功图的左下方,符合一般规律。这些都表明本文描述的定向井有杆抽油泵系统诊断模型的建模方法是正确可行的,数学模型应用是可靠的,能够支持基于知识的故障诊断方法(如专家系统、人工神经网络等)和基于数据分析的故障诊断方法(如主元分析法、Fisher判别分析法等)[10]。

图6 地面示功图和泵功图工况Fig.6 Indicator diagram of polished rod and pump working

[1] 崔振华.有杆抽油系统[M].北京:石油工业出版社, 1994.

[2] LIU Lei-ming,TONG Chao-nan,Q IANG Jian-qin. A unifor m and reduced mathematicalmodel for sucker rod pumping[J].Computational Science ICCS2004,6:372 -379.

[3] 刘磊明,张发强,闫成玉,等.有杆抽油系统通用数学模型研究[J].石油学报,2008,29(5):769-772.

LIU Lei-ming,ZHANG Fa-qiang,YANCheng-yu, et al.Studyon a generalmathematicalmodel for suck and pumping system[J].Acta Petrolei Sinica,2008,29(5): 769-772.

[4] 王昱.有杆泵抽油井工况远程监测与故障诊断系统研究[D].武汉:武汉理工大学自动化学院,2006.

[5] 蔡道钢.有杆泵故障智能诊断方法[D].南充:西南石油大学石油工程学院,2006.

[6] 王济新.有杆抽油系统设计及诊断技术及其应用[D].南充:西南石油学院石油工程学院,2003.

[7] 李子丰,李敬元,马兴瑞,等.油气井杆管柱动力学基本方程及应用[J].石油学报,1999,20(3):87-90.

LI Zi-feng,LIJing-yuan,MA Xing-rui,et al.Fundamental equations and its applications for dynamical analysis of rod and pipe string in oil and gas wells[J]. Acta Petrolei Sinica,1999,20(3):87-90.

[8] 梁若筠.定向井有杆抽油系统诊断力学模型[J].石油矿场机械,2001,30(5):19-21.

LIANG Ruo-jun.Mechanics model for diagnosis of sucker rod pumping system for directional wells[J].Oil Field Equipment,2001,30(5):19-21.

[9] 宋开利.液力反馈型空心杆采油工艺系统工况预测模型分析 [J].石油大学学报:自然科学版,2003,27 (5):88-91.

SONG Kai-li.Models for predicting operation of hollow rod pumping system[J].Journal of the University of Petroleum,China(Edition of Natural Science),2003,27 (5):88-91.

[10] 邓晓刚,田学民.生产过程故障诊断方法研究现状及展望[J].石油大学学报:自然科学版,2005,29(6): 151-157.

DENG Xiao-gang,T IANXue-min.Present situation and prospect of process fault diagnosis technique[J]. Journal of the University of Petroleum,China(Edition of Natural Science),2005,29(6):151-157.

Modeling method for fault diagnosis to sucker rod pumping system in directional well

WANG Kai

(Faculty of Mechanical and Precision Instrum ent Engineering,Xi´an University of Technology,Xi´an710048,China)

Considering the influencesof deviation angle,az imuth angle and oilon swabbingmotion,the infinitesimalwas selected from the multistage sucker rod string of directionalwell.The infinitesimalwas analyzed.The wave equation reflecting the rod string´s dynamicmovementwas established and acted as an initial kinetic model for fault diagnosis to sucker rod pumping system.Samplingwith variable step method from the whole rod and executing a special treatment at the interface ofmultistage rod,the finite difference method solves the wave equation to obtain each expressions of displacement at homogeneity and interface positions of multistage rod.Confirming initial and boundary conditions,the expressions of displacement and load on pump plunger can be obtained by the difference and iterative computation to realize finalmodeling.Inputting the correlation data about 4 oilwells from oilfield into mathematicalmodel,and the indicator diagram of pump workingwas gotten to make a fault diagnosis.The results show that the modelingmethod is effective and the reliability of the modelwas verified. The model could support knowledge-based and data analysis-based fault diagnosismethod.

modeling analysis;sucker rod string;wave equation;indicator diagram of pump working;fault diagnosis

TE 833

A

10.3969/j.issn.1673-5005.2010.02.026

1673-5005(2010)02-0130-06

2009-05-01

陕西省教育厅科学研究基金项目(08JK391)

王凯(1973-),男(汉族),河南洛阳人,博士研究生,研究方向为有杆抽油系统动力学分析建模、测试,故障诊断与模式识别。

(编辑 韩国良)