关于树的第二个最大特征值

谭尚旺,姜静静

(中国石油大学数学与计算科学学院,山东东营 257061)

关于树的第二个最大特征值

谭尚旺,姜静静

(中国石油大学数学与计算科学学院,山东东营 257061)

树;匹配;谱半径;第二个最大特征值

1 问题的提出

设 G是具有 n个顶点的无向简单图。记 G的邻接矩阵为A(G),称 A(G)的特征多项式 det(λE -A(G))为 G的特征多项式,记为 φ(G,λ)。既然A(G)是一个实对称矩阵,于是它的特征值都是实数,不妨设它们按照不降的次序排列为

称λk(G)是 G的第 k个最大特征值,称λ1(G)为 G的谱半径。

G的两个不同边在 G中称为独立的,如果它们在G中不邻接。G的一个两两独立的边集合称为G的一个匹配,边数最多的匹配称为 G的最大匹配并且一个最大匹配的边数称为 G的匹配数。令M是 G的一个最大匹配,如果 G的顶点 v与M中的一个边关联,则称 v被M饱和;如果 G的每个顶点都被M饱和,则称M是 G的一个完美匹配。

二部图的特征值在量子化学理论中有其物理意义[1]。Cvetkovic′D M曾经指出了图谱理论的几个进一步研究的方向,其中之一就是对图进行分类和定序 (classifying and ordering graphs)[2]。既然树是特殊的二部图并且它在图论中起着重要的作用,于是研究树的图论性质与它的特征值之间的关系是有意义和必要的。

令 T(n,i)表示顶点数为 n且匹配数为 i的所有树的集合。长期以来,许多学者一直利用树的谱半径对树定序[3-7]。但是,如何利用树的其他特征值对树进行定序的研究较少。特别是利用树的第二个最大特征值对 T(n,i)中的树进行定序取得的结论更少,目前只有当 n=2i,2i+1,2i+2时有几个结论被得到[8-11]。

文献[11]中证明了下述结论:对 T∈T(4n-1, 2n-1),都有

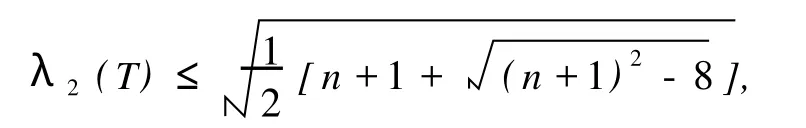
并且该上界是可达的。文献[11]中猜想:在 T(4n -1,2n-1)中,只有 4个树的第二个最大特征值能够达到该上界。本文中证明该猜想的正确性,并且对 T∈T(4n-1,2n-1),给出λ2(T)的 3个新的上界并确定达到上界的所有树。贯穿全文,令 o(G)表示图 G的顶点数,i(G)表示 G的匹配数,G≅H表示图G和H同构。特别记

引理 1[1]令 vu是树 T的一个边,则 φ(T,λ) =φ(T-vu,λ)-φ(T-v-u,λ)。

文献[5-7]中研究了 T(n,i)中树的谱半径,综合这 3个文献的结论有下面的引理。

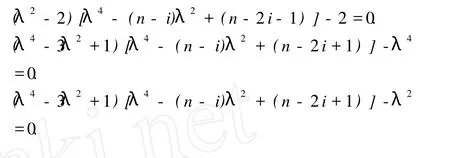
图 1 谱半径最大的前六个树Fig.1 The first six trees with the largest spectral radius

引理 4[1]令 G是顶点数为 n的无向图,V′是G的一个 k点子集,G-V′表示从G中删去V′中的所有顶点以及与 V′中的点关联的所有边后得到的 G的子图,则

2 主要结论及证明

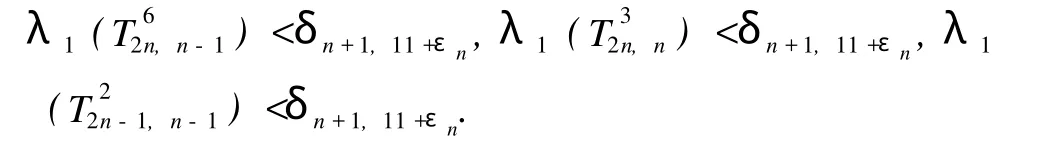
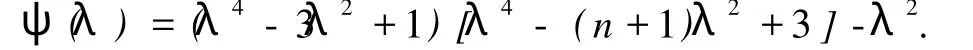
由于

由引理 2知,λ1(T32n,n)是方程φ(λ)=0的最大正根,其中

由于

由引理 2知,λ1()是方程ω(λ)=0的

最大正根,其中

由于

令Wj(j=1,2,…,20)是图 2中所示的树,记ξj=λ(λ2-1)2n-j, θ(s,t)=λ4-sλ2+t.

图 2 T(4n-1,2n-1)中的 20个树Fig.2 Twenty trees ofT(4n-1,2n-1)

由引理 1,容易得到λ2θ(2,1)]-(λ2-1)θ(n,1)θ(n,2)}.

引理 6 如果 n≥8,则

(1)λ2(Wj)=δn+1,8,j=1,2,3,4。

(2)δn+1,11+εn<λ2(W7)<λ2(W6)<λ2(W5)< δn+1,8,其中λ2(W5),λ2(W6)和λ2(W7)依次是下面方程的第二大正根:

(3)λ2(Wj)<δn+1,11+εn,j=8,9,…,20.

证明 (1)对 j=1,2,3,4,容易发现

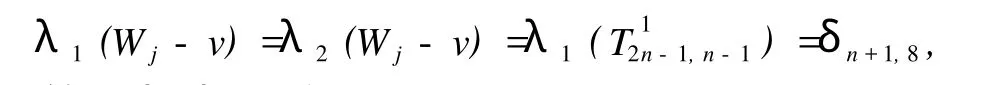
并且由引理 4知,

因此,λ2(Wj)=δn+1,8。

于是 f(λ)的 4个正根分别位于区间 (0,βn+1,4), (βn+1,4,μ), (μ,δn+1,10), (δn+1,10,+∞)内,即

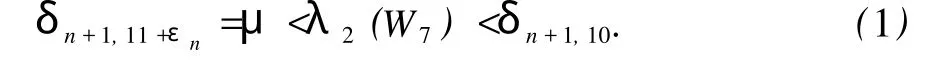
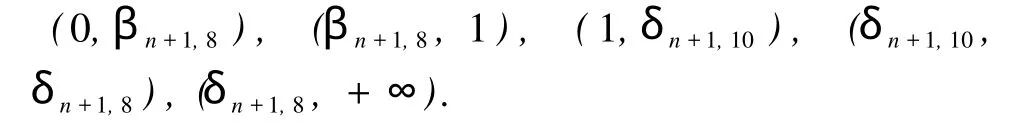
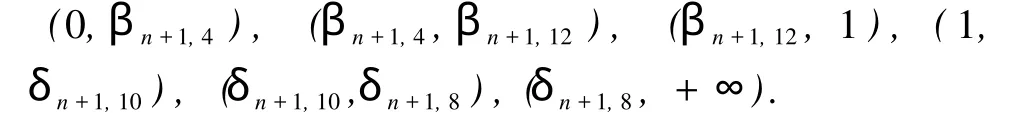
因此,对 j=5,6,有

由 φ(W5,λ)和 φ(W6,λ)得

于是对δn+1,10<λ<δn+1,8,都有 φ(W5,λ)>φ(W6, λ)。因此,由上面的讨论得

由式 (1)和式 (2)知,δn+1,11+εn<λ2(W7)<λ2(W6) <λ2(W5)<δn+1,8。

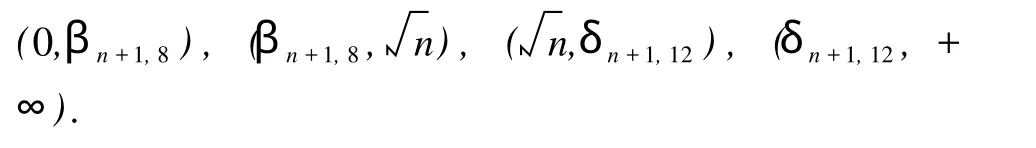
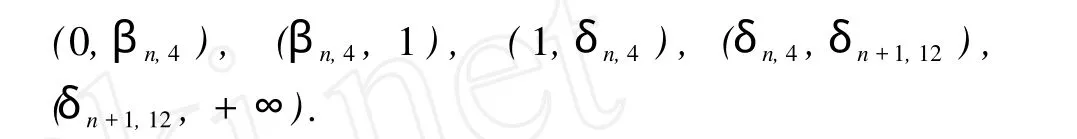
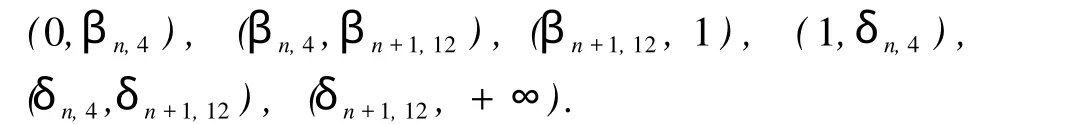
由上面的讨论,对 j=8,9,…,20,都有λ2(Wj)< δn+1,11+εn。

引理 7 令 T是一个树,o(T)≤2n-2并且 T至多有两个顶点不被它的某个最大匹配M饱和。如果 n≥6,则λ1(T)<δn+1,11+εn。

证明 如果 o(T)是奇数,记 o(T)=2s-1,则 s≤n-1且 i(T)=s-1。由引理 2得

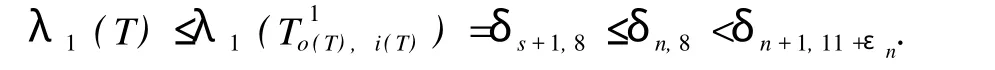
如果 o(T)是偶数,记 o(T)=2s,则 s≤n-1且 i(T) =s,s-1。由引理 2得

定理 1不仅证明了文献 [11]中提出的猜想是正确的,而且也给出了λ2(T)的 3个新的上界。

定理 1 令 n≥9,Jk={Wj:j=1,2,…,k}并且T∈T(4n-1,2n-1)。

(1)λ2(T)≤δn+1,8,并且等式成立,当且仅当 T∈J4。

(4)如果 T∉J6,则λ2(T)≤λ2(W7),并且等式成立,当且仅当 T≅W7。

证明 假设 T∉J20,由引理 6,只需要证明下式:

在引理3中取 k=2n-1,则存在一个顶点 v∈V(T),使得 T-v的每个分支,记为 Tj(j=1,2,…,l),都有 o(Tj)≤2n-1。由引理 4得

如果 Tj有完美匹配,记 o(Tj)=2sj,则 i(Tj)=sj≤n -1。由引理 2得

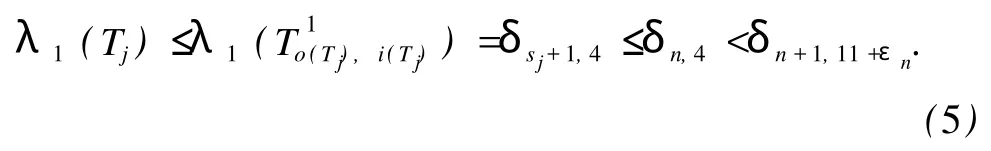
令M是 T-v的一个最大匹配,则 T-v至多有两个顶点不被M饱和。区分下面 3种情形。

情形 1 设 T-v的每个顶点都被M饱和。

对 j=1,2,…,l,因为每个 Tj有完美匹配,所以式(5)都成立。因此,由式 (4)知,式(3)成立。

情形 2 设 T-v有两个顶点不被M饱和并且它们在 T-v的同一个分支中。

不失一般性,假设 T1有两个顶点不被M饱和,而 T-v的其他分支 Tj(j=2,3,…,l)都有完美匹配。令 o(T1)=2s1,则 s1≤n-1且 i(T1)=s1-1。由引理2得

因此,结合式(5)和式(4)知,式(3)成立。

情形 3 设 T-v有两个顶点不被M饱和并且它们在 T-v的不同分支中。

不失一般性,假设 T1和 T2都各有一个顶点不被M饱和,而 T-v的其他分支 Tj(j=3,4,…,l)都有完美匹配。对 j=1,2,令 o(Tj)=2sj-1,则 sj≤n且 i(Tj)=sj-1。

对 j=1,2,如果 sj≤n-1,则由引理 2得

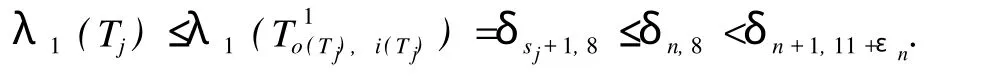
对 j=1,2,如果 sj=n且 Tj,则由引理2和引理5得

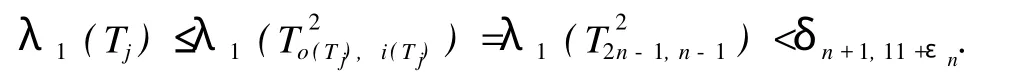
因此,当 T1并且 T2时,由式 (5)和式 (4)知,式 (3)成立。不妨设 T1≅。令u是 v在 T1中的唯一邻接顶点,则存在 T-u的一个分支,比如说,包含并且 o()=2n,而 T -u的其他分支,比如说(j=2,3,…,r),都满足o()≤2n-2。令是 T-u的一个最大匹配,则对 j=1,2,…,r,至多有两个顶点不被 ~M饱和。由引理4得

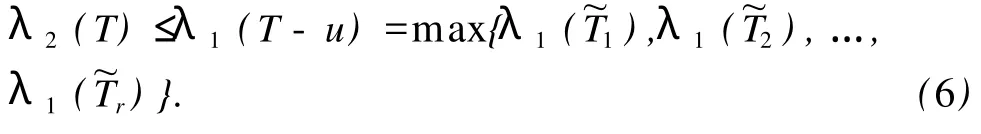
由引理 7,对 j=2,3,…,r,都有

如果则 T∈J16,这与 TJ20矛盾。因此于是由引理 2和引理 5得λ1()≤ λ1()<δn+1,11+εn。因此,由式 (6)和式 (7)知,式(3)成立。

根据上面 3种情形,完成了式(3)的证明。

注释:当 n=8时,用 2.945 19代替引理 5～7和定理 1中的δn+1,11+εn,相应的结论也都成立。因此,定理 1的结论对 n=8也成立。

[3] HOFMEISTER M.On the two largest eigenvalues[J]. LinearAlgebra Appl,1997,260:43-59.

[4] CHANGA,HUANGQ X.Ordering trees by their largest eigenvalues[J].Linear Algebra Appl,2003,370:175 -184.

[5] HOU Y P,L I J S.Bounds on the largest eigenvalues of treeswith a given size of matching[J].Linear Algebra Appl,2001,342:203-217.

[6] 谭尚旺,郭纪明.树的最大特征值 [J].石油大学学报:自然科学版,2002,26(6):113-117.TAN Shang-wang,GUO Ji-ming.The largest eigenvalue on trees[J].Journal of the University of Petrolum (Edition ofNatural Science),China,2002,26(6):113 -117.

[7] 谭尚旺.给定边独立数的树的谱半径的新上界 [J].广西工学院学报,2008,19(1):13-17.

TAN Shang-wang.On the new upper bounds of spectral radius of trees given edge independence number[J]. Journal of Guangxi Unversity of Technology,2008,19 (1):13-17.

[8] GUO J M,TAN SW.A conjecture on the second largest eigenvalue of a tree with perfect matchings[J].Linear Algebra Appl,2002,347:9-15.

[9] GUO JM,TAN SW.A note on the second largest eigenvalue of a tree with perfectmatching[J].LinearAlgebra Appl,2004,380:125-134.

[10] 谭尚旺,郭纪明.树的第二个最大特征值[J].数学研究与评论,2004,24(3):541-548.

TAN Shang-wang,GUO Ji-ming.The second largest eigenvalues of trees[J].Journal of Mathematical Research and Exposition,2004,24(3):541-548.

[11] TAN Shang-wang,GUO Ji-ming.The second largest eigenvalue of trees[J].Australasian Journal of Combinatorics,2006,34:313-320.

[12] SHAO J Y.Bounds on the kth eigenvalues of trees and forests[J].LinearAlgebra Appl,1991,149:19-34.

(编辑 修荣荣)

On the second largest eigenvalue of trees

TAN Shang-wang,J IANG Jing-jing
(College of M athem atics and Computational Science in China University of Petroleum, Dongying257061,China)

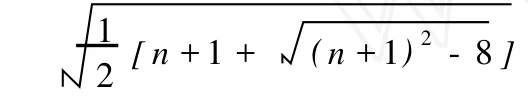
trees;matching;spectral radius;the second largest eigenvalue

O 157.5

A

10.3969/j.issn.1673-5005.2010.02.035

1673-5005(2010)02-0169-06

2009-06-20

国家自然科学基金项目(10871204)

谭尚旺(1965-),男(汉族),山东泰安人,教授,硕士,研究方向为图论。