反演变换在调和函数研究中的应用

赵天玉，刘 庆

(长江大学信息与数学学院，湖北 荆州 434023)

反演变换在调和函数研究中的应用

赵天玉，刘 庆

(长江大学信息与数学学院，湖北 荆州 434023)

反演变换也称逆矢径变换，有着比较独特的几何性质，是一种有效的数学方法，其应用十分广泛。首先给出了反演变换的定义，然后利用反演变换和凯尔文(Kelvin)变换重点讨论了调和函数的一些性质及其应用,并给出了8个相关命题及其证明。

反演变换；调和函数；凯尔文(Kelvin)变换

反演变换也称逆矢径变换，有着比较独特的几何性质，在几何[1,2]、复变函数[3]和求解静电场的电位分布中有广泛的应用[4～6]。实际上，在求解球形域和圆形域内调和方程第一边值问题的格林函数时，就用到了反演变换[7]。研究调和函数的性质时也常常用到反演变换。笔者首先给出了反演变换的定义，然后利用反演变换和凯尔文(Kelvin)变换重点讨论了调和函数的一些性质及其应用。

1 反演变换

定义1设T为空间R3上的一一变换，记以O为球心，R为半径的球面为B(O，R)，对空间中异于O的点A，在OA或OA的延长线上取一点A′，使得：

OA·AO′=R2

在T变换下，点A对应点A′，则称T为关于球面B(O，R)的空间反演变换，记作A′=T(A)。

相应地，称点A′为点A关于球面B(O,R) 的反演点，称B(O,R)为反演球面，O为反演中心，R为反演半径。

显然，点A也是点A′的反演点，称点A和点A′关于球面B(O,R)互为反演点。

规定：球心O与无穷远点关于球面B(O,R)互为反演点。

在球面坐标下，设球心O在原点，点A的坐标是(r，θ，φ)，ρ=R2/r，点A′的坐标是(ρ，θ，φ)，则点A′就是点A关于球面B(O,R)的反演点。

平面反演变换的定义与空间反演变换的定义类似，只要将球心改为圆心，球面B(O，R) 改为圆周C(O,R)即可。在极坐标下，设圆心O在原点，点A的坐标是(r，θ)，ρ=R2/r，点A′的坐标是(ρ，θ) ，则点A′就是点A关于圆周C(O,R)的反演点。

定义2设F为Rn(n≥3)上的一一变换，记以O为球心的单位超球面为B(O,1)，对Rn中异于O的点x，记：

ξ=x/|x|2

在F变换下，点x对应点ξ，则称F为Rn中关于单位球面的反演变换，记作ξ=F(x)。

相应地，称点ξ为点x关于单位球面的反演点，称O为反演中心。

显然，点x也是点ξ的反演点，称点x，点ξ关于单位球面互为反演点。

规定：球心O与无穷远点关于单位球面互为反演点。

2 调和函数的性质

性质1设平面区域Ω为圆周C(O，R) 以外的无界区域，它的反演区域为Ω1。u(r,θ)是Ω中有界的调和函数，函数：

v(ρ，θ)=K[u(r,θ)]=u(R2/ρ，θ)

称为函数u(r,θ)的凯尔文(Kelvin)变换，这里ρ=R2/r。则函数v(ρ，θ)在区域Ω1中除去原点O外是调和的。

证明由反演变换的定义可知，当M=(r,θ)在Ω中变化时，M1=(ρ，θ)在Ω1中变化。由于u(r,θ)在区域Ω中调和，故:

Δr,θu=urr+(1/r)ur+(1/r2)uθθ=0

(1)

令r=R2/ρ，显然当r≠+∞时，ρ≠0。利用复合函数的求导法则可得：

vρ=-(R2/ρ2)urvρρ=(2R2/ρ3)ur+(R4/ρ4)urr

vθ=uθvθθ=uθθ

代入形如式(1)极坐标下的拉普拉斯算子表达式可得：

Δρ，θv=(R4/ρ4)Δr,θu=0

故v(ρ，θ)在区域Ω1中除去原点O外是调和的。

性质2设空间区域Ω整个地包含在以原点O为球心、R为半径的球面B(O，R)中，u(r,θ，φ)是此区域中的调和函数，其中(r,θ，φ)表示Ω中动点M的球坐标。记ρ=R2/r，点M1=(ρ,θ,φ)是点M关于球面B(O,R)的反演点。以Ω1表示Ω的反演区域，则函数:

v(ρ,θ,φ)=(R/ρ)u(R2/ρ，θ，φ)

(2)

是区域Ω1中的调和函数(无穷远点除外)。

证明由反演变换的定义可知，当M=(r,θ,φ)在Ω中变化时，M1=(ρ，θ，φ)在Ω1中变化。由于u(r,θ,φ)在区域Ω中调和，故:

Δr,θ，φu=urr+(2/r)ur+(1/r2)uθθ+[cosθ/(r2sinθ)]uθ+[1/(r2sin2θ)]uφφ=0

(3)

令r=R2/ρ，显然ρ≠0，利用复合函数的求导法则可得：

vρ=-(R/ρ2)u-(R3/ρ3)ur

vρρ=(2R/ρ3)u+(4R3/ρ4)ur+(R5/ρ5)urr

vθ=(R/ρ)uθvθθ=(R/ρ)uθθ

vφ=(R/ρ)uφvφφ=(R/ρ)uφφ

代入形如式(3)球坐标下的拉普拉斯算子表达式可得：

Δρ,θ,φv=(R5/ρ5)Δr,θ,φu=0

故v(ρ,θ,φ)在区域Ω1中除无穷远点外是调和的。

性质3设空间区域Ω为球面B(O，R)以外的无界区域，u(r,θ,φ)在Ω中调和，函数v(ρ,θ,φ)的表达式如式(2)，称为函数u(r,θ,φ)的凯尔文(Kelvin)变换，记为：

v(ρ，θ,φ)=K[u(r,θ,φ)]

则函数v(ρ,θ,φ)在区域Ω的反演区域Ω1中除去原点O外是调和的。

证明由反演变换的定义知，区域Ω1在球面B(O，R)的内部，由于Ω是无界区域，区域Ω1包含原点O。函数v(ρ，θ,φ)在区域Ω1中调和的验证同性质2类似，只是注意当r≠+∞时ρ≠0。故函数v(ρ,θ,φ)在区域Ω的反演区域Ω1中除去原点O外是调和的。

性质4设Ω为Rn(n≥3)中的有界区域，记ξ=x/|x|2为x关于单位球面的反演点，Ω1={ξ|ξ=x/|x|2，x∈Ω}。假设u是定义在Ω上的函数，它的凯尔文(Kelvin)变换是定义在Ω1上的函数:

K[u(x)]=v(ξ)=|ξ|2-nu(x)x=ξ/|ξ|2ξ∈Ω1

则u是Ω上的调和函数当且仅当v(ξ)是Ω1上的调和函数。

证明记φ(ξ)=|ξ|2-n,ξ∈Ω1，易知φ(ξ)是Ω1上的调和函数，即Δξφ=0。经计算知:

Δξv=φΔξu+2ξφξu+uξφ

容易求得:

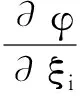
代入上式可得：

Δv(ξ)=|ξ|-n-2Δxu(x)=|x|n+2Δxu(x)

由上式可以看出，如果u是Ω上的调和函数，那么v(ξ)是Ω1上的调和函数。反之亦然。

附注：若Ω包含原点O，则Ω1是无界区域。要求v(ξ)在Ω1上调和，且当|ξ|→+∞时，v(ξ)=O(|ξ|2-n)。

3 应 用

命题1通过凯尔文(Kelvin)变换，可将平面Dirichlet外问题化为Dirichlet内问题。

证明设所给的Dirichlet外问题为：

(4)

并设闭曲线Γ内部的区域为Ω。若Ω′包含原点O，可通过坐标的平移变换，使原点落在Ω内，并不改变u的调和性。因此下面的证明都假定原点O在Ω内。

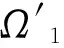
(5)

其中f1(ρ，θ)=f(R2/ρ,θ)。下面讨论v(ρ,θ)在原点的调和性。

由于：

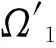
故平面Dirichlet外问题(4)可化为Dirichlet内问题(5)。

命题2通过凯尔文(Kelvin)变换，可将空间Dirichlet外问题化为Dirichlet内问题。

证明设所给的Dirichlet外问题为：

(6)

并设闭曲面Γ内部的区域为Ω。若Ω′包含原点O，可通过坐标的平移变换，使原点落在Ω内，并不改变u的调和性。因此下面的证明都假定原点O在Ω内。

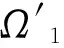
(7)

其中f1(ρ，θ，φ)=(R/ρ)f(R2/ρ,θ,φ)。下面讨论v(ρ,θ,φ)在原点的调和性。

由于：

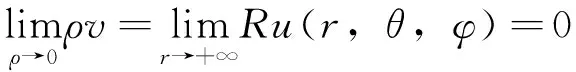
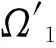
故Dirichlet外问题(6)可化为Dirichlet内问题(7)。

命题3空间无界区域上的调和函数u(M)及其偏导数ur(M)若在无穷远处趋于零，那么u(M)=O(1/r)，ur(M)=O(1/r2)(r→+∞)。这里r=|OM|。

证明由命题2的证明过程知，当u(r,θ,φ)在无界区域内调和，在无穷远处趋于零时，u(r,θ,φ)的凯尔文(Kelvin)变换函数：

v(ρ,θ,φ)=K[u(r,θ,φ)]=(R/ρ)u(R2/ρ,θ,φ)

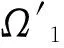
|(r/R)u(r,θ,φ)|≤A

即：

|u(r,θ,φ)|≤c/r

这就证明了：

u(M)=O(1/r) (r→+∞)

又v(ρ,θ,φ)在原点的邻域内调和，由调和函数的解析性定理[7]知，v(ρ,θ,φ)在原点的邻域内可展开成ρ的幂级数，即:

v(ρ,θ,φ)=(R/ρ)u(R2/ρ,θ,φ)=A0+A1ρ+A2ρ2+…+Anρn+…

(8)

其中，Ai(i=0,1,2,…)是与ρ无关的有界量。令r=R2/ρ，代入式(8)可得：

u(r,θ,φ)=(A0R)/r+(A1R3)/r2+(A2R5)/r3+…+(AnR2n+1)/rn+1+…

两边关于r求偏导数得：

ur=-{(A0R)/r2+(2A1R3)/r3+(3A2R5)/r4+…+[(n+1)AnR2n+1]/rn+2+…}

即：

ur(M)=O(1/r2) (r→+∞)

命题4设Ω为Rn(n≥3)中的有界区域，u(x)为Ω外的调和函数，在无穷远处趋于零，则：

u(x)=O(|x|2-n(|x|→+∞)

证明由于坐标平移变换不改变u(x)的调和性，不妨假设Ω包含原点。记：

D=RnD1={ξ|ξ=x/|x|2，x∈D}

则u(x)是D上的调和函数，D1是有界区域。

考虑u(x)的凯尔文(Kelvin)变换:

K[u(x)]=v(ξ)=|ξ|2-nu(x)x=ξ/|ξ|2ξ∈D1

由命题7知，v(ξ)是D1lt;FounderNodename0}上的调和函数，并且ξ=0为v(ξ)的孤立奇点。由于:

故当ξ→0时，v(ξ)=o(|ξ|2-n)。利用调和函数的可去奇点定理[8]知，ξ=0是v(ξ)的可去奇点，从而v(ξ)在D1内有界。即存在正常数C，使得：

|v(ξ)|≤Cξ∈D1

也就是当|x|足够大时有:

||x|n-2u(x)|≤C

因此:

u(x)=O(|x|2-n(|x|→+∞)

[1]张水胜，李祥林，刘彩平. 空间反演变换及性质[J]. 高师理科学刊，2000，20(1)：7～8.

[2]李邦荣，何艳平. 反演变换的解析式及其应用[J].高等函授学报(自然科学版)，1998，(4)：58～59.

[3]倪秀芳，李祥林. 复平面上反演变换的性质[J].阜阳师范学院学报(自然科学版)，1994，(2)：42～46.

[4]苏文杰. 几种特殊带电金属导体的空间电势分布[J]. 苏州科技学院学报(自然科学版)，2008，25(3)：37～41.

[5]苏文杰. 一种碟形金属导体外部空间的电势分布[J]. 重庆工学院学报(自然科学版)，2007，21(7)：114～118.

[6]宁布. 三维反演在静电学中的应用[J].内蒙古师范大学学报(自然科学汉文版)，1998，27(4)：278～283.

[7]谷超豪. 数学物理方程[M].第2版.北京：高等教育出版社，2002.68～95.

[8]王明新，王晓光. 数学物理方程学习指导与习题解答[M].北京：清华大学出版社，2007.173～229.

[编辑] 洪云飞

O174

A

1673-1409(2009)03-N001-04

2009-05-23

赵天玉(1958-)，男，1981年大学毕业，硕士，教授，现主要从事数学方面的教学与研究工作。