基于集对分析理论的水安全评价方法研究

高军省，高绣纺，潘红忠

(长江大学地球化学系，湖北 荆州 434023)

基于集对分析理论的水安全评价方法研究

高军省，高绣纺，潘红忠

(长江大学地球化学系，湖北 荆州 434023)

针对当前水安全研究的热点问题，从集对分析理论出发，探讨了评价等级标准确定条件下的水安全评价方法。建立了待评地区(或区域)的水安全状态与不同水安全等级间的联系度表达式，依据水安全评价指标的实际值与各等级标准界限值的关系，确定了差异度系数的取值，计算了联系数，并据此进行了水安全状态的综合评价。实例的水安全综合评价及其对比分析说明了该方法的可行性。

水安全；综合评价；集对分析；联系度；联系数

随着全球人口的剧增和社会经济的快速发展，人类社会对水的需求日益增加，同时人类的生产和生活活动对水资源及其循环系统也产生了诸多不利影响，致使水问题成为制约社会经济发展的主要因素之一。在此情况下，从20世纪90年代开始，国际有关组织实施了一系列的与水相关的研究计划，从不同角度或多或少地对水资源及水安全问题给予关注[1]。到目前为止，尽管对水安全的描述各种各样，还没有统一公认的定义[2]，但对水安全状态的评价已经成为水安全研究方面的热点之一，其研究内容包括水安全评价指标体系的构建，水安全评价标准的确定和水安全评价方法的研究等。就评价方法而言，从不同的基础理论出发进行评价，就形成了不同的水安全评价方法(或评价模型)，如模糊优选模型[3]、模糊物元模型[4,5]、遗传投影寻踪-理想点插值模型[6]、综合指数模型[7]和集对分析方法[8,9]等。

集对分析是我国学者赵克勤先生于1989年提出的用联系度统一处理确定与不确定系统的一种理论和方法。自该理论及方法提出到现在，已经在自然科学研究与工程技术领域、哲学与社会经济等领域得到了广泛地应用[10]。下面，笔者从集对分析理论出发，结合水安全评价问题，提出了一种确定联系度表达式中差异度系数的方法，进而利用联系数对水安全等级标准已经确定条件下的水安全状态进行综合评价。

1 集对分析方法

集对是指有一定联系的2个集合所组成的一个对子。集对分析是在一定问题背景下，对所研究的2个集合(即集对)的所有特性进行全面分析，总共得到N个特性，其中有S个特性是2个集合共同具有；在P个特性上2个集合相对立，在余下的的F(F=N-S-P)个特性上既不对立，也不共同具有，则称S/N为2个集合在所研究问题下的同一度(用a表示)；F/N为2个集合在所研究问题下的差异度(用b表示)；P/N为2个集合在所研究问题下的对立度(用c表示)，并统一表示为：

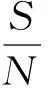
或

μ=a+bi+cj

(1)

式中，μ称为2个集合的联系度；i为差异度系数，在[-1,1]区间取值，有时仅起差异标记作用；j为对立度系数，计算时恒取-1，有时仅起对立标志作用；a+b+c=1。

2 评价方法

2.1基本思路

根据集对分析的理论及其特点，从便于理解和容易计算同一度、差异度、对立度的角度出发来构造集对分析中的联系度表达式；结合水安全评价指标的实际值与水安全标准各等级之间的关系，确定差异度系数i的取值(对立度系数j恒取-1)，从而计算出联系数；根据联系数的大小进行水安全等级的评定。

2.2评价步骤

1) 单指标评价 根据某地区(或区域)水安全评价指标的实际值与水安全评价标准进行对比，按照单指标法判断水安全等级，作为进行综合评价的基础。

2) 构造联系度表达式 将待评价的某地区(或区域)的水安全状态与水安全评价标准中的各级标准组成不同的集对，构造某区水安全状态与水安全标准各等级间的联系度表达式。

参照文献[11]，对于某等级水安全标准来说，若单指标的评价结果落入该等级范围内视为同一，落入相邻的等级范围内视为差异，落入相隔等级范围内视为对立。根据联系度的定义式和单指标评价结果，计算同一度、差异度和对立度，写出待评价的水安全状态与水安全标准各等级间的联系度表达式：

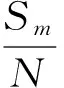
(2)

式中，μm为某区水安全状态与第m(m=1，2，…，M)等级水安全标准之间的联系度；M为水安全评价标准的等级个数；N为水安全评价指标的总数；Sm为单指标评价结果是m等级的指标个数；Fm为单指标评价结果是(m-1)或(m+1)等级的指标个数；i为差异度系数，取值范围为[-1，1]；Pm为单指标评价结果是(m-2)或(m+2)等级的指标个数；j为对立度系数。

3) 确定差异度系数i的取值 对于某区的水安全状态与第m级标准的联系度来说，当水安全评价指标的实际值落入第(m-1)级时，按式(3)计算i值；当水安全评价指标的实际值落入第(m+1)级时，按式(4)计算i值。

(3)

(4)

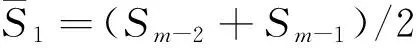
4) 计算联系数 将差异度系数的取值和对立度系数的取值(恒取-1)代入到所建立的联系度表达式中，计算出联系数，得到待评地区(或区域)的水安全状态与水安全标准各等级间的联系数的数值。

5) 综合评价 依据联系数的数值大小进行水安全状态的等级评判。

3 实例分析

文献[12]建立了3层(目标层、准则层和指标层)、5个准则(生命安全、经济安全、生态环境安全、社会安全和管理安全)共19个指标的水安全评价指标体系，并将水安全状态分为5个等级，其分级标准和各指标的实际值见表1。笔者以表1中的数据为基础，用上述方法对其水安全状态(程度)进行综合评价。

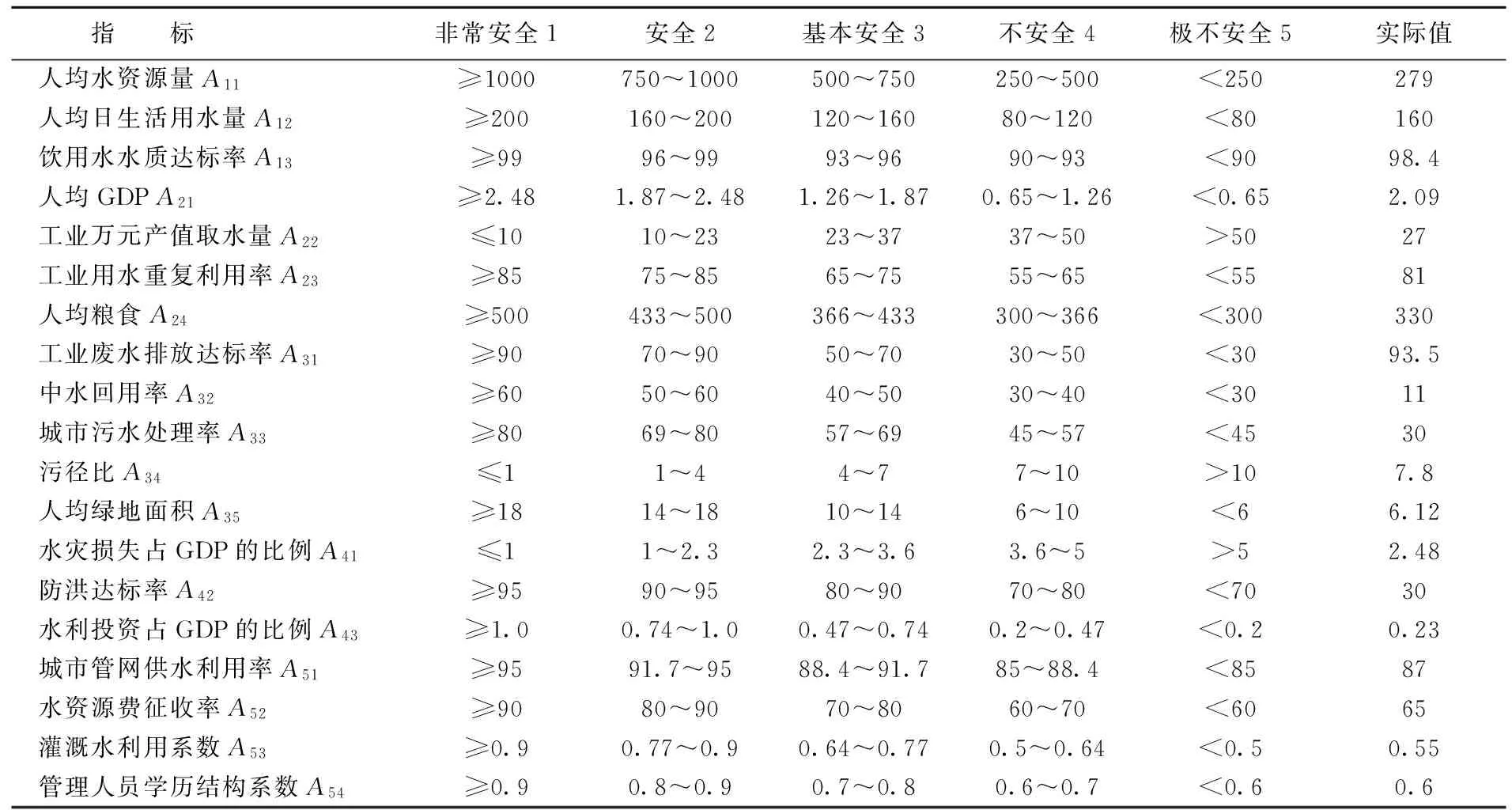
表1 水安全等级划分标准与评价指标实际值

按照评价步骤，首先得到单指标评价结果，见表2。从表2中可以看出，单指标的评价结果相差很大，必须进行多指标的综合评价，才能得出较为合理的评价结论。水安全状态与水安全标准各等级的联系度如表2所示。

表2 水安全的单指标评价结果与联系度

联系度综合反映了各个评价指标与评价结果的关系。根据集对分析理论，差异度系数i的取值在[-1,1]之间，对立度系数j可恒取-1。因此在未确定i的取值时，就难以用联系度来进行水安全等级的判别。

在确定差异度系数i的取值时，若不考虑评价指标的实际值，仅考虑i的3个特别值，即取-1、0和1，则相应的联系度计算结果如表3。水安全状态的评价结果依次为4级、4级和3级。由此可见差异度系数的不同取值对评价结果的影响。

事实上，在水安全评价中应充分考虑评价指标的实际值。针对不同的水安全评价指标，将其实际值分别代入到式(3)或式(4)中求得i值，对应代入到联系度表达式中，计算得到该例的水安全状态与水安全标准各等级间的联系数，结果如表3。依据联系数最大原则，水安全评价结果为4级。

表3 评价实例的水安全状态与水安全标准各等级的联系数

上述评价结果是在不考虑各评价指标权重的条件下得出的。文献[12]采用模糊数学方法进行了水安全评价，考虑了5个评价准则的权重和每一个评价指标的权重，其评价结果为“隶属于3级，但处于3级与4级的临界状态”。这与笔者的评价结果相差不是很大。

另外，笔者所提出的基于集对分析理论中的联系数的综合评价方法是在单指标评价基础上建立评价问题的联系度表达式，并根据评价指标的实际值与各个等级标准间的关系来确定差异度系数值，进而计算出联系数。这比文献[11]的直接构造联系数计算公式的方法更符合集对分析思想，也容易被人们理解和采用。对于模糊数学方法来说，由于过分强调最大值和最小值(这由模糊运算规则所决定)的作用，往往会丢掉一些中间有用的信息。而笔者所提出的方法则不会出这样的问题。

4 结 语

笔者应用集对分析理论，通过确定联系度表达式中的差异度系数取值，计算出联系数，据此对水安全状态进行了评价。通过实例应用和评价结果的比较分析，所用方法有一定的可行性和优越性，通过进一步考虑各评价指标的权重，是可以用于水安全状态(程度)的评价。

[1]畅明琦，黄强.水资源安全理论与方法[M].北京：中国水利水电出版社，2006.13～18.

[2] 陈绍金.水安全辨析[J].中国水利，2004，17：13～15.

[3] 韩宇平，阮本清，解建仓.多层次多目标模糊优选模型在水安全评价中的应用[J].资源科学，2003，25(4)：37～42.

[4] 李如忠.模糊物元模型在区域水安全评价中的应用[J].水土保持研究，2005，12(5)：221～223.

[5] 陈鸿起，汪妮，申毅荣，等.基于欧式贴近度的模糊物元模型在水安全评价中的应用[J].西安理工大学学报，2007，23(1)：37～42.

[6] 童芳，董增川，邱德华.区域水安全系统评价新方法探析[J].水利水电科技进展，2008，28(2)：30～34.

[7] 孙才志，迟克续.大连市水资源安全评价模型的构建及其应用[J].安全与环境学报，2008，8(1)：115～118.

[8] 卢敏，张展羽，石月珍.集对分析法在水安全评价中的应用研究[J].河海大学学报(自然科学版)，2006，34(5)：505～508.

[9] 金菊良，吴开亚，魏一鸣.基于联系数的流域水安全评价模型[J].水利学报，2008，39(4)：401～409.

[10] 赵克勤.集对分析及其初步应用[M].杭州：浙江科学技术出版社，2000.114～190.

[11] 李祚泳，丁晶，彭荔红.环境质量评价原理与方法[M].北京，化学工业出版社，2004.317～320.

[12] 王远坤，夏自强，曹升乐.水安全综合评价方法研究[J].河海大学学报(自然科学版)，2007，35(6)：618～621.

[编辑] 洪云飞

X824

A

1673-1409(2009)03-N044-04

2009-06-02

国家水体污染控制与治理科技重大专项课题(2008ZX07010-006-003)。

[作者简介]高军省(1964-)，男，1986年大学毕业，博士，副教授，现主要从事水资源利用与保护方面的教学与研究工作。