SiF基态分子(X2Πr)的解析势能函数

赵 俊，张昆实

(长江大学物理科学与技术学院，湖北 荆州 434023)

SiF基态分子(X2Πr)的解析势能函数

赵 俊，张昆实

(长江大学物理科学与技术学院，湖北 荆州 434023)

利用群论及原子分子反应静力学的有关原理, 推导了SiF分子基态的电子态和合理的离解极限, 并利用Gaussian 03 程序包, 采用 QCISD (T)和B3P86方法结合D95 (3df, 3pd), cc-PVTZ, 6-311g**和6-311++g (3df, 3pd)基组，对SiF分子的基态X2Πr平衡结构和谐振频率进行了优化计算。通过比较计算结果，发现B3P86方法为最优方法、D95 (3df, 3pd)为最佳基组。使用该方法和基组对SiF分子的基态进行了单点势能扫描计算，并采用正规方程组拟合 Murrell-Sorbie函数,得到了SiF分子基态完整的解析势能函数,计算出了SiF分子的光谱常数ωe、ωexe、Be和αe的值。

SiF；分子结构和势能函数；基态；Murrell-Sorbie函数

双原子分子势能函数是研究分子反应动力学的关键[1,2]，同时又是构造多原子分子全空间势能函数的基础[3，4]，随着光化学、分子生物学、天体物理、激光物理以及纳米技术的发展，势能函数尤其是双原子分子势能函数的精确研究引起了科学界越来越多的重视[5，6]。因此,从理论计算的角度导出双原子分子基态的势能函数一直是较重要的研究课题。基态双原子分子的Murrell-Sorbie[7]函数是一种较好的势能函数形式，笔者在前一阶段的研究中，采用这种势能函数形式研究BeO分子取得了较好的结果[8]。下面，笔者继续利用这种函数形式,在简要推导SiF分子基态离解极限后,采用密度泛函理论中的B3P86方法计算并比较了6-311++g (3df,3pd)，D95(3df,3pd)，cc-PVTZ 和6-311g**基组[8,9]对SiF分子的基态(X2Πr)平衡几何结构和谐振频率的影响。用优选出的D95 (3df,3pd)基组,结合B3P86方法对基态进行单点能扫描计算,应用单点能计算的结果拟合出SiF分子的基态势能函数,并推导出光谱常数。

1 SiF分子的离解极限

SiF分子为线性双原子分子,属C∞V群。要获得其基态(X2Πr)的正确势能函数,必须确定出合理的离解极限。

Si原子的基态为3Pg，F原子的基态为2Pu,均属SO(3)群,当2个基态Si、F原子反应生成SiF分子时, Si、F原子的对称性降低, SO(3)群的不可约表示分解为C∞V群的不可约表示:

3Pg→3Σ-+3Π2Pu→2Σ++2Π

(1)

通过对组合Si(3Pg)+F(2Pu)的直积和约化:

(3Σ-+3Π)⊗(1Σ++1Π)→2,4Σ-+2,4Π+2,4Σ++[2,4Σ-]+2,4Δ

容易看出最后结果中含有SiF分子的X2Πr，根据微观过程的可逆性原理[9],分子基态电子态的合理离解极限为:

SiF(X2Πr)→Si(3Pg)+F(2Pu)

(2)

2 理论计算

2.1基组的优选

利用Gaussian03程序[3]进行能量计算,即使采用同一计算方法,不同的基组对基态及激发态的能量计算结果仍有较大影响。笔者选用Gaussian03软件包中的QCISD(T)方法和B3P86方法，在D95(3df,3pd)，cc-PVTZ，6-311g** 和6-311++g (3df, 3pd)基组下优化比较计算了SiF分子的基态X2Πr的平衡结构和谐振频率。所得结果如表1所示。通过综合比较与分析，在所采用的4个基组中，只有B3P86方法结合D95 (3df,3pd)基组的计算结果与实验值[10]最接近。因此，接下来的SiF分子基态单点能扫描计算也是基于这种方法进行的。

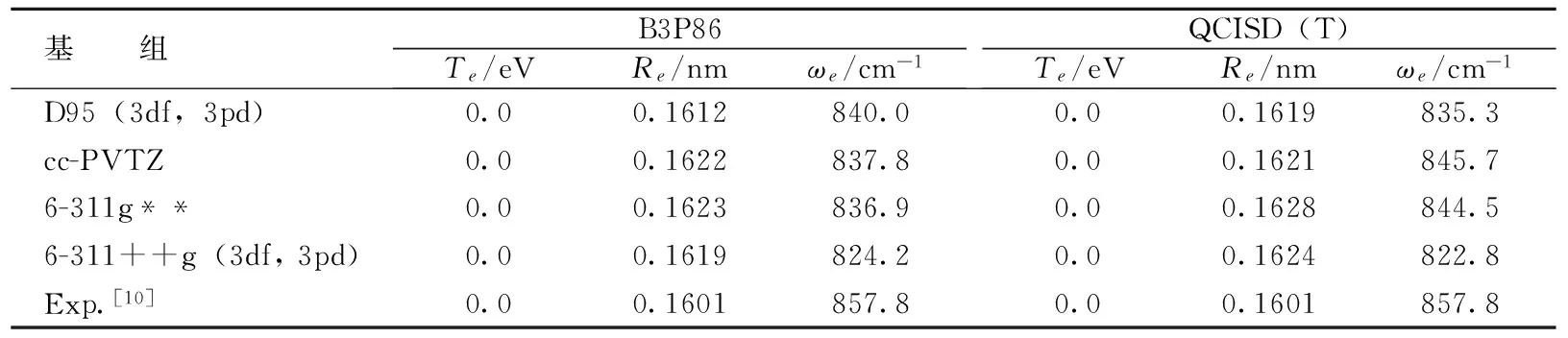
表1 SiF分子X2Πr态的优化计算结果

2.2理论计算拟合SiF分子基态势能函数及光谱常数计算

采用B3P86/D95(3df,3pd)对SiF分子基态进行单点能扫描计算,扫描计算过程中使用的各种参数，除Si原子和F原子的核间距在不断改变外, 其他与结构优化时保持严格一致, 得到X2Πr态的一系列单点势能值后,用Murrell-Sorbie函数(简称M-S势能函数)：

V=-De(1+a1ρ+a2ρ2+a3ρ3)exp(-a1ρ)

(3)

图1 SiF分子的基态X2Πr的势能曲线

进行最小二乘拟合。式中，De为离解能；ρ=R-Re；R为核间距；Re为平衡核间距；a1，a2，a3为拟合参数，拟合结果列于表2。

根据Ml-S势能函数拟合的势能曲线如图1。其中,实线为正规方程组拟合得到的结果,圆圈为单点能扫描结果。由图1和表2可以看出，能量扫描得到的X2Πr态的离解能与拟合得到的结果几乎完全一致，其他位置处的点和线也符合得很好。因此，拟合出的M-S势能函数正确地表达了SiF分子的基态势能函数。

为便于进一步分析比较，下面用M-S势能函数来推导SiF分子的基态分子光谱常数。根据势能函数与各阶力常数的关系：

(4)

由式(3)可以推导出力常数f2，f3，f4的表达式分别为：

(5)

(6)

(7)

将式(5)～(7)代入势能函数的拟合参数，便可计算SiF分子2阶、3阶及4阶力常数，结果见表2。

表2 SiF分子X2Πr态的M-S势能函数

根据力常数与光谱常数的关系[11]，可计算出SiF基态的光谱常数ωe，ωexe，Be，αe(ωe和ωexe分别为谐振频率和非谐振频率，Be和αe分别为刚性转动因子和非刚性转动因子)。相应的公式如下:

(8)

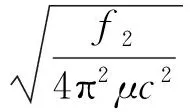
(9)

(10)

(11)

式中，μ为分子的约化质量；c为光速,计算结果列于表3中。从表3可以看出，笔者计算出的SiF分子基态电子态的平衡核间距、离解能和各光谱常数，均与实验值符合得非常好。

表3 SiF分子的光谱常数

3 结 语

笔者利用原子分子反应静力学的原理，推导出了SiF分子基态电子态的离解极限。并用不同方法对SiF分子的基态X2Πr平衡结构和谐振频率进行了优化计算。使用优选出的D95(3df,3pd)基组，结合B3P86方法对基态电子态进行了单点能扫描计算，拟合出了M-S势能函数，并将理论计算结果与光谱试验数据进行了比较。结果表明，基态各光谱常数与试验结果吻合得很好，同时，单点计算势能值与拟合值在较大的核间距变化范围内能够很好地吻合，在吸引支能够出现无限接近能量零点的势能平台，并且可以趋近于无穷大的核间距，因此该势能函数能够正确地反映双原子分子的离解极限和长程势，为分子动力学研究提供了很好的解析势能函数。

[1]Horst M A T，Schatz G C，Harding L B.Potential energy surface and quasi-classical trajectory studies of the CN+H2reaction[J ].J Chem Phys，2001, 105(2): 558～5721.

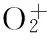
[3] Zivny O, Czernek J.CCSD ( T) calculation of vibrational frequencies and equilibrium geometries for the diatomics F2，SF and their ions[J ].Chem Phys Lett，1999, 308: 165～1681.

[5] 施德恒,戴启润,王栋臣，等.7LiH 分子X1Σ+态的平衡几何、谐振频率、离解能及其解析势能函数[J].信阳师范学院学报(自然科学版)，2006,19(2):144～147.

[6] 王栋臣, 熊宝库,戴启润，等.7LiH 分子的基态X1Σ+和激发态A1Σ+、B1Π与b3Π的平衡几何与垂直激发能[J].信阳师范学院学报(自然科学版)，2006,19(2):148～152.

[7] Murrell J N, Sorbie K S.New analytic form for potential energy curve stable diatomic states[ J ].J Chem Soc Faraday Trans, 1974, 2(70):1552～1554.

[8]赵俊,张昆实.BeO分子基态(X1Σ+)的势能函数研究[J].长江大学学报(自然科学版)，2008,5(2):N15～17.

[9] 朱正和.原子分子反应静力学[M].北京:科学出版社,1996.

[10] Huber K P, Herzberg G.Molecular Spectra andMolecular Structure IV Constants of DiatomicMolecules[M].New York: VanNostrand Reinhold Company, 1978.

[11] 朱正和,俞华根.分子结构与分子势能函数[M].北京:科学出版社,1997.

[编辑] 洪云飞

O561.4

A

1673-1409(2009)03-N010-03

2009-01-22

赵俊 (1981-), 女，2004年大学毕业，硕士，现主要从事原子与分子物理方面的研究工作。