小学数学“解构教材”的基本路径

朱旭平

小学数学“解构教材”包括两层含义：一是解读小学数学教材，二是在解读基础上，根据数学本身的知识逻辑体系，根据学生的年龄特点和认知体系，对教材进行二次构建，从而形成教学设计思路。所以，对教材的“解”与“构”是互为依存，有着递进关系的一组概念，解读教材是实现教材二次建构的基础，而教材的二次建构又反过来深化对教材的理解，两者有着诸多相同的研究视角、途径和策略。本文从具体的课时案例出发，深入阐述小学数学教材解构的基本路径。

一、着眼知识的发展脉络。理清知识的前因后果

解构人教版小学数学第十册12～13页内容“因数和倍数”。笔者碰到的最大问题是：如何出示因数和倍数这一组概念。浏览此课现有教案，一般都是从2x6=12这道算式中，用规定方式引出的。

而许多学生看到此课题，他的第一感知是：因数在乘法中出现过，我们已经学过了。那么，这两个因数概念有着怎样的关系呢?考察教材变化，因数、倍数概念从具有整除关系的除法算式中揭示，改为从相应的乘法算式na=b中揭示，将原先命名的约数概念改为因数。这样的变化，就带来了一个疑问：为什么要把原先的约数改为因数，在小学数学教材中出现命名重复现象呢?这究竟是失误、巧合，还是基于数学本质内涵而作出的规定。我们认为：乘积关系中的因数与因倍关系中的因数，两者不是蕃薯与毛竽各不相干的关系，而是蕃薯与薯条的关系。从知识发展体系看，两个因数的本质内涵是一致的，它们都可以表示数与数之间的关系，只是在不同的关系背景下其概念外延不同，在乘积关系中，因数可以表示任何数，在因倍关系中，因数只能表示非0整数。因此，我们在解构这节课时，因数、倍数这组概念的出示采用旧知迁移方式，着力于这组概念在数论背景中的刻划。

基于这样的思考，因数、倍数概念的出示方式设计如下。先顺向迁移因数概念，根据飞机图，列出算式2×6=12，让学生说算式中各部分的名称(板书：因数、因数、积)，再让学生说说2是谁的因数?6呢?(板书2和6是12的因数)进而逆向提问：12是谁的积?12是2的什么呢?(板书：12是2和6的倍数)现在，谁说说因数和倍数之间有什么关系?教师总结：因数和倍数是一组相互依存的概念，有着互逆关系。

所以，我们认为解构教材，不能孤立地看，而应以一种整体、开放、联系的视角，把教材内容纳入整个知识发展脉络之中，理解编者意图。理清整个知识发展脉络分布的基本结构。理清知识的前因后果、来龙去脉，找准新旧知识的关联点与生长点。明确每节课所学的知识点、知识块在整个单元、整册教材和整个小学阶段所处的地位与作用，明确每节课的重点、难点和关键，从而明确教学着力点。而理清知识的前因后果。既要回过头来看看前面的教材，明确现学内容的学生认知基础，又要放眼于现学内容后面的乃至中学教材中的内容，明确现学内容的高位知识是什么，以便为建构现学内容找到迁移的落脚点、巩固的深化点，为后面内容的学习扫清障碍、埋下伏笔。同时。要以此为背景，充分考虑知识的形成线索与学生的认知线索，对教材内容进行适当的补充、修改、调换和删减等。

二、梳理知识间内在关系。实现知识串联与整合

解构人教版小学数学第一册45—46页内容“6和7的加减法”，此课教学内容包括加法、减法两大块并列知识，而加减法知识内部都各自蕴含着生活原型、意义、算理、计算技能、书写规范等各个层次表征，而如何梳理加减法及内部各个层次表征之间的关系，实现知识串联与整合，糅合各层次表征的力量，促进加减法知识模块的建构。是解构本课教材碰到的最大问题。

为了破解这个问题，我们认真研读教材。仔细分析加减法本身特点及关系。具体分析如下：

第一，从书本情境(见上图)分析，加减法有各自的生活原型，每一幅图可以得到两道有着互逆关系的算式，数学上简称为“一图两式”。我们认为：加法易于从图中得出两道互逆算式，而减法不易从图中得出两道互逆算式。

第二，从加减法各自两个算式的内在关系来看，两道加法算式关系很明显，学生已初步掌握，能从一道加法算式想到与之互逆的另一道加法算式；而两道减法算式关系不清晰，学生基本没有这方面的认知基础。

第三，从计算算理看，两者都是以数的组成来阐析计算算理，但减法比加法更难理解，从计算技能看，减法比加法更难掌握。

基于这样的分析，我们认为本节课的教学重点是：掌握计算6、7加减法的计算方法，形成计算技能，能从一幅图中列出两道相应的算式；教学难点是：通过操作和观察活动，让学生在活动中发现一图两式的内在规律。在建构教学时，我们作了如下处理：

1生活原型。课始用加法生活原型引入，明晰了抽象线路：从苹果实物(具体)圆片图(半具体、半抽象)两个算式(抽象)；在课尾呈现减法生活原型，使学生在掌握减法意义、计算方法的基础上，反过来解决生活问题，为下节课的学习作铺垫。

2意义算理。本节是计算课，以算理为主，意义为辅。算理阐述以半具体、半抽象的组成图(如下图)实现图式结合，突破计算方法。不单纯阐述意义，将算式意义糅合于算理和两道互逆算式的对比分析之中，使算式意义为理解算理服务。

3教学方式。加法以引导发现为主，减法以自主探究为主，减法教学时间比加法略多一些。

所以，我们认为解构教材，要透过教材的表面现象，脱去教材漂亮的外衣。从情境、例题、习题等方面解剖出所蕴含的知识点；要从哲学的高度，厘清各个知识的特点、主次关系与逻辑关系，明确教学的落脚点；要根据教材的广度和深度，学生的认知基础和心理特点，明确哪些内容比较抽象，不易被学生理解，哪些内容纵横交错，比较复杂，哪些内容本质属性比较隐蔽，哪些内容在新旧知识衔接上呈现出较大的差距等等。从而促使解构者有效把握主体知识，破解主要矛盾，落实教学的重难点，实现知识有机串联与整合，形成教学的整体构架。

三、分析教材编排目的。处理、挖掘学习素材

解构人教版一年级第二册“两位数加一位数进位加法”，笔者对教材主题图(见下图)进行分析，认为“咱们班有33人，每人一瓶够吗?”是生活原型问题，它促使学生在生活背景中学会数学推理，什么情况下够了。什么情况下不够。激起学生寻求解决生活问题的策略。进而抽象为数学问题“一共有几瓶矿泉水?”激发学生对计算的需求，这是新课程在计算课中渗透“算用结合”的一大亮点。但从试教效果来看，“咱们班有33人，每人一瓶够吗?”这一现实问题没有引起学生足够的思维冲突和深层次思考。一半多学生一看到主题图都能马上答出24+9=33(瓶)，这就冲淡了学生

对现实问题(“咱们班有33人，每人一瓶够吗?”)的数学推理思索。

基于这样的分析，笔者认为如何突显对这一生活问题的数学推理，进而产生计算需求，体现教材的编排目的，这是本节课所面临的最大挑战。笔者从学生的认知基础出发，对主题图的呈现采用化明为暗的手法，即将上面主题图中的一箱矿泉水去掉数量24瓶，零散的9瓶把它紧密的摆放在一起，使学生数不清瓶数。这一小小改动，使这个现实问题更具有实际思考价值，更忠实于生活问题的思考原形，如分发矿泉水的学生及班内同学，在看到一堆矿泉水后，产生了问题：“每人一瓶，够不够。”这样就使学生思考点在“够还是不够”上，而不在“24+9：?”的计算层面上。从而把“够与不够”这一现实问题推向了讨论的焦点，激起学生对总瓶数和总人数进行比较，呈现出以33瓶为基点的思维方式，实现了学生对“咱们班有33人，每人一瓶够吗?”这一现实问题的完整建构，也激起学生想知道“究竟总共有多少瓶”的欲望，突显了数学推理和数学计算的现实价值。

所以，我们认为在解构一节课时，要注重处理、挖掘学习素材，从两个维度进行对比分析。一是从教材编排意图和学生认知特点等维度进行思考，要求各个部分学习素材应承担哪些功能?达成怎样的效果?二是对教材中现有学习素材进行分析，要求教师透过各个素材的表面现象，深层次分析它已经具有的功能，是否符合学生的认知特点，实施于教学将会达成怎样的效果?解构者要在两者对比中明晰差距，从中找到处理、挖掘学习素材的方向与策略，从而有效地对教材中的问题情境、教学课例、教学顺序、配套练习及呈现方式等等进行二次建构。

四、挖掘知识背景。渗透数学思想方法

人教版小学数学第九册第114页内容“身份证号码”一课，一般只是停留于对身份证号码表层含义的解读。而此课属于数学广角范畴，突显数学思维是其本质特点。所以在解构此课时，笔者把突破常规教法，增厚身份证号码的本质内涵作为构课的关键点。

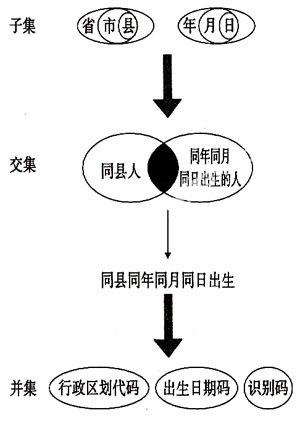
基于这样的思考，笔者对教材进行了深层次分析，认为《身份证号码》一课蕴含着两条线索。明线是身份证结构和各部分数字表征的意义；暗线是身份证的本质内涵唯一性，这是数字编码的根源，是编码方法首要思考点。这两个方面都是身份证号码这一知识载体不同侧面的体现，在教学上笔者渗透了集合思想(见上图)，形成了三个层次的认知建构，具体阐述如下：

1子集思想。用运动员号码从年级——班级——学生这样从大到小的编码策略思维，到前6位行政区划代码，7至14位出生日期码迁移。既厘清了各部分知识结构，又体现出以唯一性为基点的编码策略思维，这个过程是数学思想、方法的具体运用。

2，交集思想。针对某一具体身份证的前14位号码，教师提问：前6位表示什么?它唯一吗?7至14位表示什么?它唯一吗?它们合在一起又表示什么，它唯一吗?你感觉它的范围怎么变化?这样使学生进一步理解合在一起的前14位号码所表示的意义范围，它其实就是行政区划代码和出生日期码两个表示范围的交集。

3并集思想。从整体上解读身份证号码，明确身份证三大部分结构及各部分数字代码所表示的意义，实现身份证号码这一认知对象的整体建构。

好的数学课堂教学，最不能缺失的是让学生理解数学内容的本质与精神，也就是数学思想方法。数学思想方法是数学的灵魂，解构者要透过数学知识表层，深层次挖掘、把握概念的本质内涵。在教学中，渗透数学思想方法与解决数学问题是数学内在本质各个侧面、各个层次的体现，数学思想方法是在解决数学问题的过程中逐步形成的，并得到人们有意识的提炼和归纳，而解决数学问题的过程，也就是数学思想方法不断被运用的过程，从而不断推进学生认知体系向更高层次建构。