关于求解力学中常用关系曲线的经验公式

毛 宁

在试验研究成果中有很多关系曲线供查用，如果能把它们提高一步成经验公式，那就更可确切方便地传播引用。找经验公式的简便方法莫过于把资料点绘适用于曲线类型（直线、抛物线、双曲线等）的有关坐标纸上，例如一般的方格纸、对数纸、半对数纸等，形成直线，就可直接写其方程式的经验公式。但是有时点绘到各种函数的坐标纸上仍然是一条曲线，不能直接写出其直线关系式y＝a＋bx，注意此式中的变量x，y可以是任意函数。此时就需要把它转换成直线，再确定式中的常数a和b，或者采取转换坐标以及拟合曲线等措施。下面就选择水力学、土力学中常用的阻力系数、给水度、固结度等参数求出经验公式便于引用；同时也介绍此类曲线的求经验公式通则。

1 水中球体运动的阻力系数经验公式

图1所示为试验资料点绘的曲线，在水力学和流体力学中，例如罗斯的两本经典著作（Rouse，1938，1946）［1］，都详细讨论了阻力系数CD与雷诺数Re的关系曲线，包括有各家学者在水槽、水洞、风洞中用各种材料的球形、圆盘等做试验的成果，测定阻力F和流速V即可由下式计算阻力系数CD

流体力学中都把此CD－Re曲线划分为3段，即上段直线的层流区，下段水平线的紊流区和中间段曲线的过渡区。层流区直线段恰好符合Stokes理论公式，即CD＝24／Re；紊流区CD＝常数；只有过渡区，尚未见拟合该曲线的公式。遇到此类问题，例如研究泥沙运动在水中的下沉速度，仍是查曲线或表格，似有不便，也不协调，因此为阻力系数实验公式的完整性，补充求出过渡区的经验公式，方法过程如下：

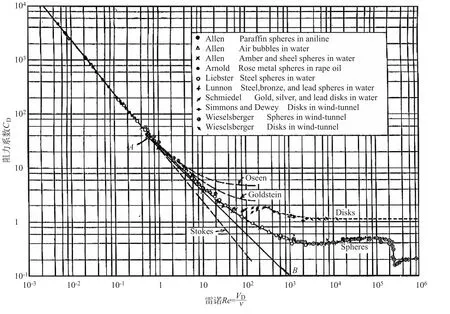
图1 阻力系数与雷诺数关系曲线Fig．1 Relation curve of drag coefficient and Reynolds number

对数纸上只要画成直线就很容易求出抛物线型和指数方程的经验公式y＝axb；对于对数纸上的曲线则可加减一个常数，画成对数纸上的直线，而再求得经验公式为

因为上式取对数即得到对数坐标纸上的直线方程为

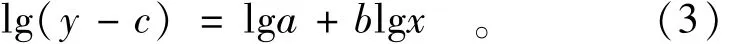
此种作法的成功是由于同一常数在对数纸上的距离是不等的，在实际点绘时，试取两三个常数即可得出满意的直线，如图1中的 AB线，取了常数 c＝－0．35，即说明此 AB直线方程的纵坐标为 y＝0．35。或者按照下式更确切计算c值为

式中：（x1，y1）及（x2，y2）为曲线上靠近两端任选的两点，再选第3点为x3＝时，可在曲线上查出相应的y3值。对照图1的坐标，x＝Re，y＝CD，则选曲线上两点 x1＝1，y1＝25；x2＝1 000，y2＝0．46，然后计算

并在曲线上查出相应 y3＝2，代入式（4）算得 c＝0．35。因而式（3）为

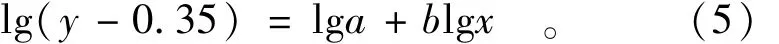
至于式（4）的引用，证明很简单，因为在曲线上的3点由式（2）为y1－c＝ax1b，y2－c＝ax2b，y3－c＝c，解出 c值即式（4）。

然后把所选曲线上的两点x1＝1，y1＝25；x2＝1 000，y2＝0．46代入式（5）解联立方程式即可求得a＝24．66，b＝－0．784。这里提请注意，如果试验的点子分散，还可将众多点子代入式（5）求a，b的平均值，或用最小二乘法求精确的a，b值。因而求得相当式（2）的方程为 y＝24．66x－0．784＋0．35，也就是图1中直线AB的y值加上c值即曲线的y值。写成CD与Re的关系，即其经验公式为

式（6）过渡区或称介流区的适用范围可取1＜Re＜2 000。关于层流区阻力的适用范围可取Re＜1；紊流区阻力可取常数CD＝0．44，适用范围Re＞2 000。这样就补充完整了球体在水中运动的阻力系数公式。

同样，在泥沙运动学中引用此球体阻力系数于水中泥沙沉降速度问题时也可补充此过渡区公式的缺陷，例如按照球体下沉阻力公式（1），F＝相等关系就可推求出以下公式，式中的沉速w就相当于雷诺数中的流速V，各流态区公式的适用范围同上。而且由适用范围也可推知各流态的泥沙特征，例如下面层流区沉速公式，在Re＜1适用范围限制内，粒径约为D＜0．1 mm的泥沙。

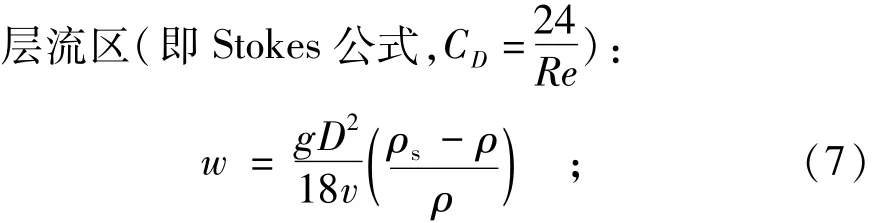
紊流区（CD＝0．44）：

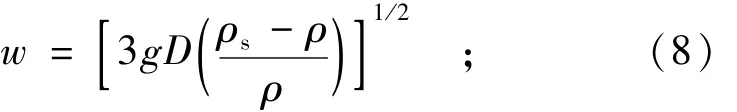
过渡区或介流区：

以上公式尺度和谐，取单位一致即可。阻力系数CD是指球体直径D的泥沙，若非球体则在非层流区成片状时，按照图1的试验资料CD应加倍。

2 土力学中沉降固结的经验公式

图2所示为太沙基的2本《土力学》（Terzaghi，1943，1948）［2］中的垂向沉降固结度 U与时间因子Tv的关系曲线。太沙基曾推导出单向固结问题的理论解，但为无穷级数，甚为复杂，因而把3种不同排水和固结压力的情况绘成曲线C1，C2和C3，并且找经验公式，在他的理论力学中有2页叙述，只对其中曲线C1找出分段的经验公式，即固结度U%＜52．6时为抛物线型公式，U% ＞52．6时为半对数的函数式。运用起来似不简便，而且对曲线C2和C3也没有给出经验公式。现在从实用观点出发，放弃曲线两端变化陡缓相差较大的精度，推求单一公式如下，补充完整这3条曲线的经验公式。

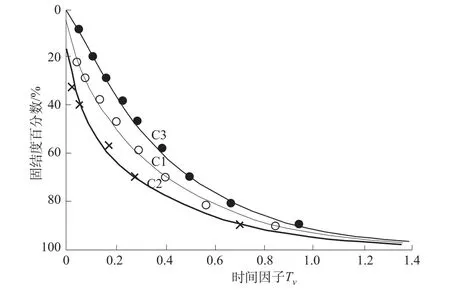
图2 固结度与时间因子关系曲线Fig．2 Relation curve of degree of consolidation and time factor

此曲线接近抛物线，可试求下面多项式方程，

具体求法以中间曲线C1为例，先在曲线上任选一点（x1＝0．4，y1＝70），并将 y坐标改换为与x对应就画成一条直线，此例即为直线方程

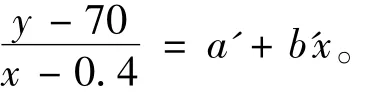
很明显，上式一乘出就是式（10）的形式。然后再选曲线上两点 y2＝30，x2＝0．07和 y3＝90，x3＝0．85代入上面直线方程联立求解常数 a＇＝128．10，b＇＝－98．42，则上式乘出即得曲线C1的经验公式为（y即 U%，x即 Tv）

y＝18．76＋167．47x－98．42x2。

同理，图 2中的曲线 C2，选点（y1＝70，x1＝0．28），（y2＝40，x2＝0．047），（y3＝90，x3＝0．715），求得常数 a＇＝134．58，b＇＝－123．92经验公式为

y＝32．32＋169．28x－123．92x2。

图2中的曲线 C3，选点（y1＝70，x1＝0．497），（y2＝30，x2＝0．155），（y3＝90，x3＝0．925），求得常数 a＇＝131．10，b＇＝－91．21，经验公式为

y＝4．84＋176．43x－91．21x2。

以上3条曲线的经验公式写成固结度U%与时间因子Tv的关系，则为

曲线C1

曲线C2

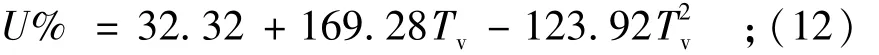
曲线C3

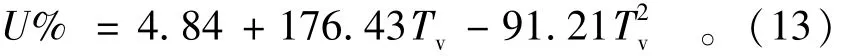
以上3式验算的各点，绘在相应的曲线上，计算点与曲线相差最大3%；其适用U%的范围：曲线C1为15%～90%，曲线 C2为25% ～90%，曲线 C3为10%～90%。

3 渗流计算中的给水度经验公式

图3所示为给水度比孔隙率μ／n与渗透系数k的试验资料点绘在半对数纸上的关系曲线，包括砂砾松散土和黏性土的室内试验资料。此曲线呈拉长的S型，由极缓上升转为急速上升后又转缓上升渐趋于平。此类曲线在土力学和泥沙学中会遇到的，例如土力学中的土粒级配颗分曲线就是此型，若能引用此法找其经验公式，似可更便于引用和计算土料的特征粒径d50，d60，d15，d85等。下面就以图3为例介绍此类型曲线的找经验公式过程。

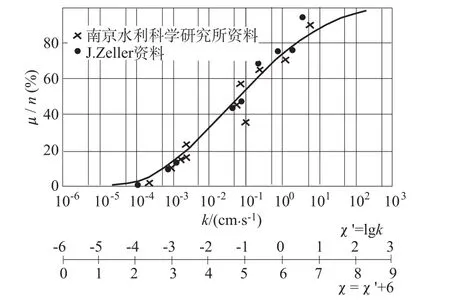
图3 给水度与渗透系数关系曲线Fig．3 Relation curve of storativity and coefficient of seepage

此类拉长S形曲线属于指数上有指数的刚泊兹（Gompertz）方程，即

如果曲线不交于坐标原点，或在x＝0处交在y轴上的值为y0且值不是很小时，则上式应为

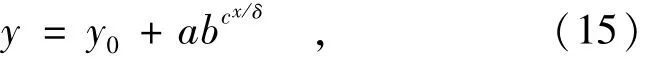
确定式（15）中常数a，b，c的方法，需按照独立变数x的等差级数（差为δ）列表分成3组，每组点数均为m个，点可沿着已绘成的曲线按所欲的等差级数选取；从表中小值开始列出的x，y与lg y等栏计算出的3组中每一组资料lg y的和分别设为S1，S2及S3。应注意，对于不交在原点上的方程式（15），lg y应以 lg（y－y0）代换。则式（15）中的3常数可用下式求得，证明见文献［3］。

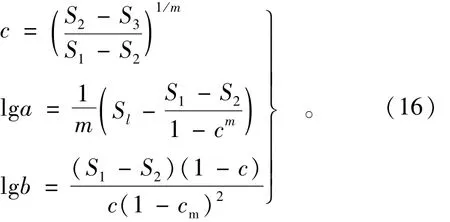
引用上式找图3所示曲线的经验公式。虽然是画在半对数纸上的，但经过转换仍可套用式（14）的形式求其经验公式。如图3的横坐标k改为对数值lg k后（lg10＝1，lg10－1＝－1，…）就转换成为等分的一般方格纸坐标x′；然后再平移原点位置转换为坐标 x（＝x′＋6），此时就可套用式（14）确定 a，b，c了。

依序选取横坐标x的差数δ＝1，在图3曲线上选点列表计算（为避免0的对数，从lg k＝－5算起）计算表如下：

表1 计算列表Table 1 Calculation

由表列lg y 3组资料每一组的和代入式（16）计算3个常数为

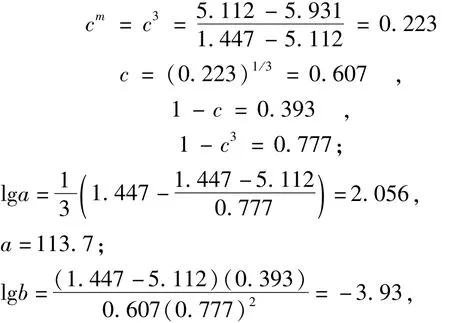
b＝0．000 117 5 。

代入式（14）得公式

y＝113．7（0．000 117 5）0．607x／δ；

因 y＝μ／n， x／δ＝6＋x′＝6＋lg k，故得

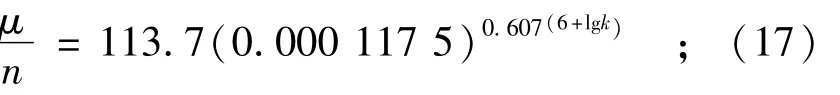
或用对数式表示

上式中k的单位为cm／s，计算出的结果是百分数，将表列最右一栏公式计算结果与表中间栏所取曲线上的值比较，可知求得公式的精度较高。现举一例：已知某中细砂 d50＝0．2 mm，干密度 γd＝1．49 g／cm3，渗透系数 k＝1．7×10－3cm／s，求给水度 μ值。将k值代入公式（17）或式（18）算得＝18．72%，因为干密度与孔隙率n和土粒质量密度γg的关系为 γd＝γg（1－n），一般 γg＝2．65 g／cm3，故可算得n＝0．438，则得给水度为 μ＝0．187 2×0．438＝0．082。

4 结 语

在阅读水力学、土力学、泥沙运动学等有关文章时，感到常用的一些试验资料关系曲线，需要找出经验公式更有利于引用传播和发展。因此，选出常用的3种曲线，并且是在分析资料常用的对数纸、半对数纸、普通方格纸上所画的曲线。便于利用它们说明找经验公式的相应方法过程；同时也补缺陷，给出了水力学中的球体潜水运动阻力系数公式和泥沙沉降速度公式；土力学中的沉降固结度公式和渗流力学中的给水度公式。

在坐标纸上画曲线求经验公式，不需要高深数学，是最简便的方法，所举的3例在试验研究中常遇到带有普遍性的，尤其是拉长的S形曲线，完全类同正规分布的土粒级配颗分曲线，如能以公式取代，可能对引用特征粒径和滤层设计有一定的方便。

［1］ HUNTER R．Fluid Mechanics for Hydraulic Engineers［M］．New Youk：Dover Publisher，1961．

［2］ TERZAGHI K．Theoretical Soil Mechanics［M］．New York，Wiley，1943．

［3］ 毛昶熙．电模拟试验与渗流研究［M］．北京：水利出版社，1981．