单组裂隙压水试验的一个非稳定渗流模型

王旭升，万 力

式中：Q0和hw分别为稳定状态的压水流量和水头；L为试验段的长度；rw为井孔半径。这个公式与承压含水层Dupuit稳定井流公式一致，其中引用影响半径假设成压水试验段的长度。

当压水试验对象为裂隙比较发育的岩体时，流量随时间的变化是反映裂隙渗流机制的重要信息。而且，在整个试验过程中流量未必已经达到稳定，这种情况下使用稳定流公式就可能带来显著的误差。但是，目前的常规压水试验工作中，这种非稳定渗流资料往往被忽略，也缺少成熟的分析方法。

实际上，地下水动力学的非稳定井流理论经过70多年的发展已经比较成熟，可以在压水试验的分析中加以借鉴。这种非稳定井流理论在裂隙含水层的抽水试验中有广泛的应用。例如，针对各向异性裂隙承压含水层，Hantush则利用坐标变换法把一系

压水试验是我国水利水电工程中用来确定裂隙岩体渗透性的基本试验方法。在进行压水试验时，一般假设灌注压力恒定足够长时间之后，注入流量将达到一个稳定值，并用它计算岩体透水性参数。压水试验的直接结果是岩体的单位吸水量，而不是岩体的渗透系数。这是由于岩体具有各向异性，无法用一个数值表示不同方向的渗透性。不过，在《水电水利工程钻孔压水试验规程》［1］中，还是提供了一个经验公式来计算岩体的参考渗透系数：列各向同性抽水井流公式转变为各向异性条件下的井流公式［2］，Way提出了利用抽水试验确定三维渗透张量的方法［3］，Barcker［4］，Dershowitz和 Doe［5］还发展了用分维描述的裂隙含水层抽水试验理论。定流量抽水试验往往并不适用于基岩山区的调查，使这些理论的应用受到限制。但是，可以选择近似满足压水试验条件的其他井流模型进行分析。

妨碍地下水动力学在岩体水力学中应用的关键问题，在于传统的地下水动力学基本上描述的是多孔介质而非裂隙介质的渗流行为。当我们使用地下水动力学概念分析裂隙岩体渗流时，需要处理单裂隙渗流-应力耦合规律与地下水渗流方程之间的过渡。张祯武等曾提出定压力变流量压水试验的三维非稳定流模型［6］，使用的也是多孔介质假设，没有解释模型与裂隙独特行为之间的物理联系。本文的目的是通过单组裂隙渗流、应力 应变的基本特征和定量描述，建立压水试验水动力学模型，促进非稳定压水试验数据的分析利用。

1 模型假设及方程

将单组裂隙的压水试验简化为图1，即在裂隙1中通过压水孔注水，驱动裂隙水发生非稳定渗流。裂隙1与裂隙2和3相互平行且垂直间距相同，裂隙1中的地下水可通过隙间岩体流向裂隙2和3中，见图1（a）。模型的基本假设条件：相对压水试验的影响范围而言裂隙可视为无限延伸；天然条件下裂隙岩体处于饱和静水压力状态；裂隙1无充填；压水试验过程中在裂隙1内只发生平行裂隙面的径向流，水压力是径向距离的函数，见图1（b）；隙间岩体近似为均匀多孔介质。当压水试验段包含若干平行裂隙时，裂隙1也可以代表多条裂隙构成的组合裂隙。

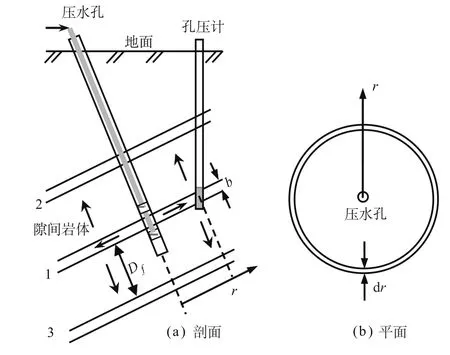
图1 单组裂隙压水试验模型示意图Fig．1 Simplified diagram of water injecting test on a group of fracture

1．1 裂隙水流连续性方程

假设裂隙岩体的应力场和渗流场在压水孔周围具有轴对称性质，则根据质量守恒的原理，裂隙1中水流连续性条件可描述为

式中：r为离开压水孔中心的径向距离；t为时间；ρw为裂隙水的密度；q为距离r处裂隙水单位弧长的流量；ε为裂隙1与周围岩体的水量交换强度；bv为裂隙的平均隙宽。对于微观上不均匀分布的隙宽b（x，y），定义平均隙宽为

式中：Ω为局部范围的面积；A为隙宽积分平均值趋向平稳的参考面积。在本模型中，假定参考面积足够小，且平均隙宽在天然状态下是均匀的。

设裂隙水运动处于层流状态，则单宽流量可根据Darcy定律描述为

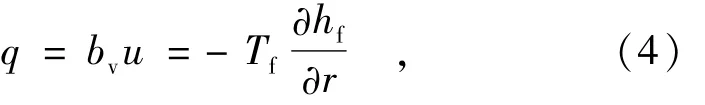
式中：u为裂隙水的流速；hf是裂隙水的水头增量；Tf为裂隙的导水系数，可根据立方定律计算。hf表示压水试验过程中裂隙水头与天然水头的差。将式（4）代入式（2）得到

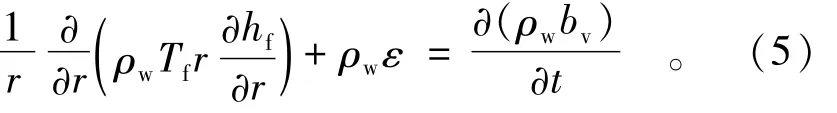
1．2 应变渗透耦合效应

在裂隙水压力的变化过程中存在应变渗透耦合行为，即裂隙宽度的变化将引起裂隙水透水能力的变化，而裂隙透水性的变化又可以影响到裂隙水压力的变化，从而改变裂隙的有效应力状态。在前人的研究中，裂隙透水性的变化既可以直接表示为法向有效应力的函数，又可以通过隙宽对法向有效应力的响应间接表示。本模型采用隙宽的变化进行间接描述。

裂隙的有效法向应力σe（以压应力为正）可表示为

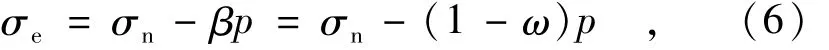
式中：σn为上覆岩体荷载形成的裂隙面法向总应力；p是裂隙水的压强；β为水压力系数；ω为隙面闭合率。水压力系数反映了裂隙面局部闭合接触所产生的影响。隙面闭合率ω＝1－β是本模型引入的参数，用来反映裂隙面的闭合接触程度，并假设它和平均隙宽一起都与有效法向应力存在唯一关系。隙宽随有效应力的变化描述为

式中 Kn为裂隙的切线法向刚度，可以随应力水平而变化。在法向总应力σn保持不变的情况下，可以推导出

其中

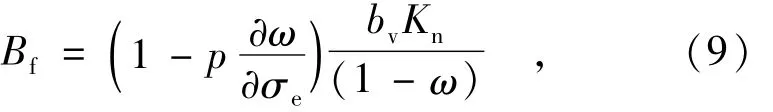
式中参数Bf为隙宽的水压力响应系数，而ω／bv反映了闭合率随平均隙宽的变化。

1．3 隙间串流

隙间岩体可以使平行裂隙1，2，3之间发生串流，串流强度就是裂隙1与周围岩体的水量交换强度。假设隙间串流可用Darcy定律进行简单描述：

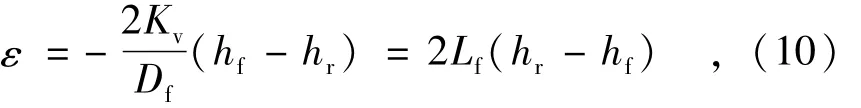
式中：Kv为隙间岩体在垂直裂隙1方向的渗透系数；Df为隙间距；Lf＝Kv／Df为窜流系数；hr为裂隙 2和3的水头增量。当裂隙1中的水压力足够大时，可引起周围岩体的结构面扩张，导致其透水性变化，表现为Lf的增大。当Lf＝0时表示地下水只在单组裂隙中流动。

1．4 裂隙水的贮存量变化

水压力的变化将引起裂隙水密度的变化，设裂隙水具有线弹性变形特征，则

式中Bw是裂隙水的体积模量，与压缩系数成反比。

裂隙水贮存量的变化反映在式（5）的右端项，是裂隙张开度变化和裂隙水密度变化的共同结果，根据式（8）和式（11）有

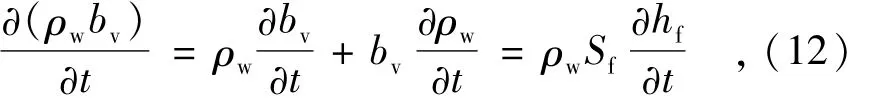
其中

为裂隙贮水系数（无量纲）。

1．5 定解条件

假设裂隙水密度的变化为小量，综合式（5）、（10）和（12），裂隙1的水动力学方程可最终描述为

当压水试验段穿越多片裂隙时，可将多片裂隙合并处理为一片等效裂隙，此时裂隙1的Tf和Sf反映的是多片裂隙的叠加值。

模型以压水孔试验段的压力作为边界条件，即

式中hw为试验段水头增量。而距离压水孔无穷远处的边界条件可表示为

裂隙1的初始静水压力状态可描述为

式（15）～（17）构成求解裂隙水流方程（14）的定解条件。

从压水孔进入裂隙1的流量Qw用下式计算：

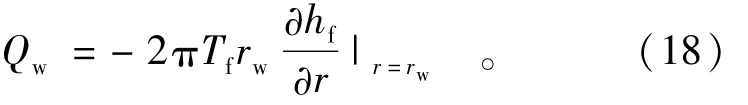
2 模型的求解和应用

上述定解模型的严格求解需要考虑Tf，Sf，Lf等参数和相邻裂隙水头hr在压水试验过程中的变化，比较复杂。但是，也可以在某些简化条件下获得简单的解析解。假设在某个压水阶段，参数Tf，Sf，Lf近似保持不变，且相邻裂隙的水压力仍然保持静水压力状态，即hr＝0，则上述压水试验的非稳定渗流模型与地下水动力学［7］中第一类越流系统的定降深井流问题具有相似性，借用Hantush［8］获得的解析解，裂隙1水头增量随径距和时间的变化可表示为以下方程：

其中

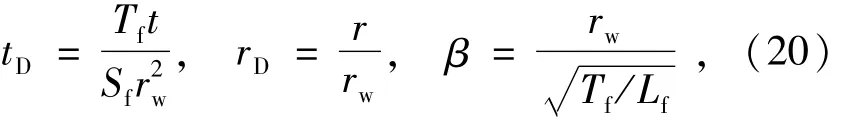
而W（tD，rD，β）为一个含有积分的函数。根据式（18），井孔注入流量为

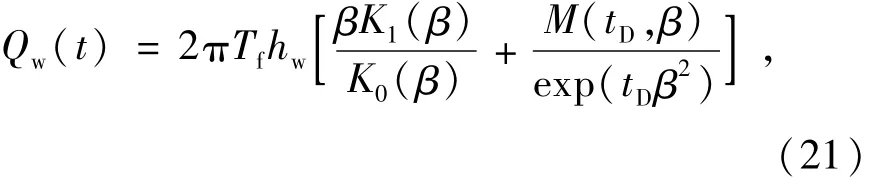
其中K0（β）和K1（β）分别为虚宗量0阶和1阶第二类Bessel函数。M（tD，β）是一个特殊函数

其中J0（u）和 Y0（u）分别为0阶第一类和第二类Bessel函数。这个函数表明流量随着时间的推移逐渐减小。常规压水试验主要关心近似稳定状态的流量，从上述解析解可以得到当时间很长时水头增量和流量都将趋于稳定值，并有

利用试验观测到的流量变化曲线反求参数的方法，是拟合（Q0→Qw）／Q0随时间变化曲线，该曲线满足方程

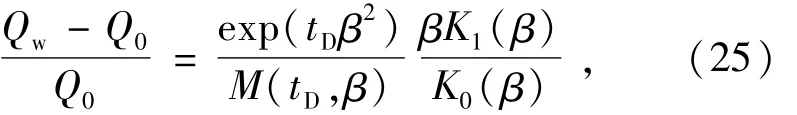
一般取对数时间曲线进行分析。

下面将上述解析解用于分析一个在瑞典进行的压水试验。该压水试验资料见于瑞典核燃料和废料管理公司（SKB）的报告［9］，试验对象为花岗岩，钻孔编号为KLX17A，进行了多段压水试验。本次分析的试验段为深度107～127 m，这一深度存在一个裂隙发育密集的破碎带［10］，非充填裂隙的最大密度达到22 m－1，平均密度为9 m－1。试验段直径7．6 cm，压力水头201 kPa，测得压入流量的稳定值为12．1 L／min。流量的变化曲线以及利用式（25）获得的拟合曲线见图 2，反演得到参数：Tf＝0．028 m2／h，Sf＝1．45×10－3，β＝0．008 3。根据平均裂隙密度，试验段约有180条裂隙，因此对应单片裂隙的参数为：Tf＝1．57×10－4m2／h，Sf＝8．03×10－6。

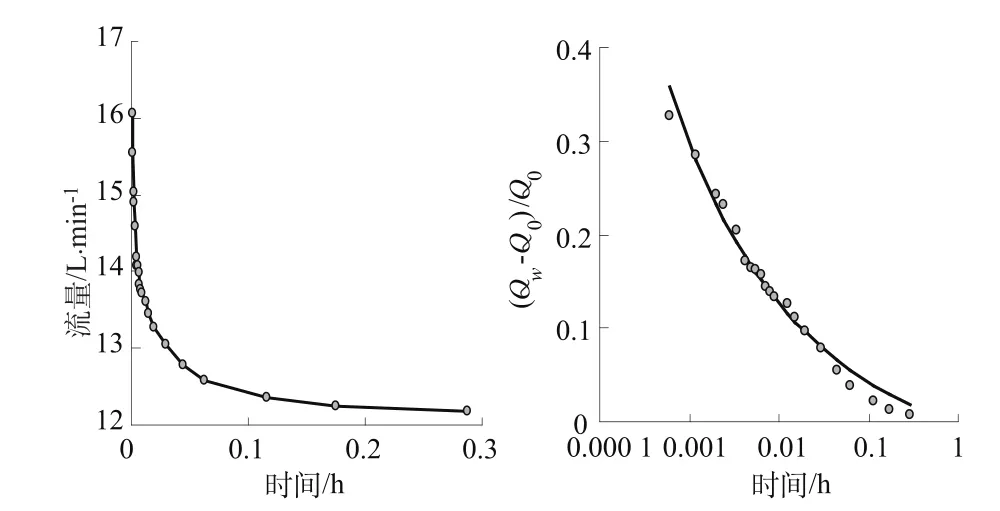
图2 某花岗岩压水试验数据（左）和拟合曲线（右）Fig．2 Water injecting test on some granite rock：measured data（left）and fitting curve（right）

3 讨 论

常规压水试验分析所得到的渗透系数并非岩体的水平渗透系数。这一点可以通过上述模型加以说明。当β很小时，即隙间岩体透水性较差时，式（24）可以近似改写为

根据规范，压水试验获得的透水率（单位吸水量）为

其中γw为水的容重。如果取平行裂隙方向的岩体平均渗透系数为Kh，有Tf＝KhL，则

这说明压水试验得到的透水率不仅和平行裂隙方向的岩体渗透系数有关，还受到垂直裂隙方向岩体渗透性（隐含在β参数中）的影响。对比式（1）和式（27），有

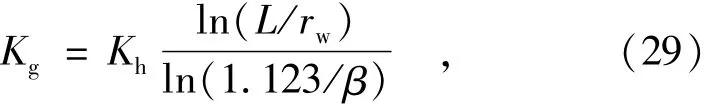
两者的差别取决于岩体裂隙串流参数β，β越小，Kg相对Kh越偏小；反之则可能偏大。上述瑞典花岗岩试验段有 β＝0．008 3，因此 Kg＝1．28 Kh，偏大约28%；若 β＝0．001，则 Kg＝0．89 Kh，偏小约 11%。这种偏差可以通过非稳定压水试验分析进行判断。

简单解析解比较适用于压力相对较小的单次压水试验，分阶段压水试验的逐次分析可以得到不同的参数，将能够反映不同压力水平裂隙渗透、变形特征。本文模型特别适用于分析断裂带这种具有优势产状结构面的非稳定压水试验。对于高压压水试验，需要在模型中考虑变形－渗透耦合效应的非线性变化，可以利用数值模拟等更复杂的方法进行求解。

［1］ DL／T 5331－2005，水电水利工程钻孔压水试验规程［S］．

［2］ HANTUSH M S．Analysis of Data from Pumping Tests in Anisotropic Aquifers［J］．Journal of Geophysical Re－search，1966，71（2）：421－426．

［3］ WAY SC，MCKEE C R．In－situ Determination of Three－dimensional Aquifer Permeabilities［J］．Ground Water，1982，20（5）：594－603．

［4］ BARKER JA．A Generalized Radial－flow Model for Pum－ping Test in Fractured Rock［J］．Water Resources Re－search，1988，24（10）：1796－1804．

［5］ DERSHOWITZ WS，DOE T W．Analysis of Heterogene－ously Connected Rock Masses by Forward Modeling of Fractional Dimension Flow Behavior［J］．International Journal of Rock Mechanics and Mining Sciences，1997，34（3／4）：652－663．

［6］ 张祯武，李兴成，徐光祥．利用定压力非稳定流压水试验求水文地质参数［J］．岩石力学与工程学报，2004，23（15）：2543－2546．

［7］ 陈崇希，林 敏．地下水动力学［M］．武汉：中国地质大学出版社，1999．

［8］ HANTUSH M S．Non－steady Flow to Flowing Wells in Leaky Aquifers［J］．J．Geophys．Res．，1959，64（18）：1043－1052．

［9］ ENACHESCU C，van der WALL R，WOLF P．Hydraulic Injection Tests in Borehole KLX17A，Subarea Laxemar，Oskarshamn Site Investigation［R］．Stockholm：Swedish Nuclear Fuel and Waste Management Co，2007．

［10］ CARLSTEN S，MATTSSON K J，STR?HLE A，et al．Geological Single－hole Interpretation of KLX17A and HLX42，Oskarshamn Site Investigation［R］．Stockholm：Swedish Nuclear Fuel and Waste Management Co，SKBP－07－209，2007．