水位降落条件下非稳定渗流试验研究
段祥宝,谢罗峰
1 概 述
大量工程资料和实践经验表明:水库或江河水位降落过快过深,会导致上游边坡失稳发生滑坡。诱发滑坡的根本原因是边坡中发生非稳定渗流。非稳定渗流由于其渗流方向的特殊性和渗流场的复杂性,在实际工程设计和计算中尚不能够完全得到有效地确定和重视。目前在工程实践中,多以简化处理非稳定渗流,有时会产生较大误差。用这样的结果来进行边坡稳定分析、指导工程设计和建设是非常危险的。因此,对库水位降落下的非稳定渗流复杂流态开展研究非常重要。
砂模型不仅能够真实反映渗流的物理现象,而且能够反映非稳定渗流过程中的边坡稳定情况。砂模型在渗流研究中被广泛应用[1-3]。毛昶熙等进行了非稳定渗流的砂槽模型试验,比较了多种渗流数学模型[1]。余湘娟等通过长江砂的宽水槽模型模拟了河流边坡在高水位退落时的崩岸和稳定,分析了多种因素对退水速度判别指标的影响[4]。段祥宝等通过宽槽和窄槽的模型试验,模拟了洪峰过程中堤岸的非稳定渗流过程[5]。朱伟等在河流土堤内进行了非稳定渗流的现场试验,实测了洪水来临时河堤内的渗流进展过程[6]。由于非稳定渗流场的特殊性,前人在非稳定渗流试验研究中,对水位降落过程中的退水指标k/μv研究较少,对渗流于边坡的影响原因研究也不够。
本文开展了粉砂、细砂、壤土、黏土等典型土质不同坡比的水槽模型试验,模拟了水位降落过程中多种工况下的非稳定渗流场变化过程,分析了边坡内部孔隙水压力值、渗透坡降分布以及浸润线在不同降速的退水过程中的变化特征。并在试验结果的基础上探讨了自由面最高点及浸润线计算方法。
2 试验方法
2.1 试验装置
2.1.1 模型水槽
模型试验在5 m×0.3 m×0.8 m的水槽中进行。水槽边壁为嵌于水槽钢架内1.25 m×0.8 m的钢化玻璃,便于观察水槽内试样的变化情况。水槽顶部安装有水平导轨,在其上安装有可在导轨上水平移动的千分表,结合模型正面的高清摄像机可以观测模型试验过程中模型试样各部位的沉降和变形。如图1、图2所示。
2.1.2 上下游进出水系统
在水槽模型的前侧安装有水位控制系统,包括安装有竖井式溢流装置的3 m×2 m水箱两组,上下游各一组,可以控制上下游侧水位;水箱底部安装有进水控制阀一组,可控制水位上升的速度和进水流量;下游安装出水控制阀一组,可以调节水位降落的速度和出水的流量。同时使用可以调节水位升降的速度,自由控制上下游水位变化过程。
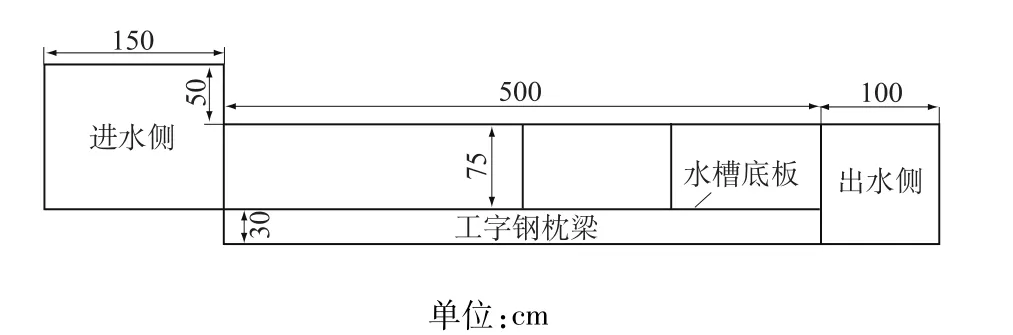
图1 水槽结构示意图Fig.1 The structure diagram of sand flume

图2 砂槽模型正向图Fig.2 Front view of the sand flume
2.1.3 测量设施
在水槽的钢板一侧安装有紫铜管,外接渗压计或测压管,测量坡体内部的瞬时孔隙水压力。在下游侧另安装有可以量测渗流量的控制阀出口,可以计量渗流量的大小。
2.2 试验方法
试验主要模拟水位降落条件下的边坡非稳定渗流场对水位降落速度的动态响应过程。试验中对土质边坡的模拟是重点,填筑质量是控制模型与实际堤坝及江河岸坡保持一致的关键。试验的主要过程包括以下几个方面:
(1)控制土料的干密度填筑边坡,具体的干密度指标见表1。分层填筑,填筑过程与工程上筑坝过程类似,预先计算出需要填筑的土量,每次填筑一层,并碾压每层至5 cm高度为止。直至填筑完成后做好坡面的护理和反滤。模型下游边坡反滤层如图3。

表1 试验土体材料物理力学参数Table 1 Physical parameters of the test soils

图3 模型下游边坡反滤层俯视图Fig.3 Vertical view for the inverted filter ondownstream slope
(2)用进水口侧的溢流设施模拟库(江河)水位。先在边坡中形成稳定渗流,通过控制边坡前缘的水位降落速度,模拟水位降落情况下的土坡内部非稳定渗流流场以及土坡的稳定。
(3)根据每个时刻的测值,结合边坡形状,对瞬时边坡内部渗流场的水头值进行插值,插值方法以克里格插值方法和三角形插值为主。插值所得的“零压力线”即为浸润线,或称之为渗流自由面。
(4)试验中通过多种手段对边坡进行观测,包括观察边坡中各部位有无明显位移;通过安装在水槽顶部的千分尺测量边坡顶部的沉降量;以固定在模型前方的高清摄像机记录试验过程中边坡具体变化情况。
(5)分析试验中边坡内部的渗流场分布,着重分析不同水力条件下土坡内部渗流场分布的特性以及孔隙水压力对边坡稳定的影响。
2.3 试验组次
试验选择了几种典型的边坡填筑材料。由于土体的内摩擦角的差别,设计出的各种填筑材料的边坡坡比也各有差异,如粉砂、细砂、中砂的干坡都无法在1∶1的坡比下稳定。因此,砂土坡比主要以1∶1.5和1∶2的坡比为主,黏土边坡以 1∶1为主,设计出多组试验。每组试验的降落速度都尽量包含骤降、快降、缓降的情况。
3 试验结果与分析
3.1 流场特性
上游水位降落的非稳定渗流试验是在模型土坝充分饱和且形成稳定渗流的基础上进行的。在上游水位降落初期,稳定渗流场的平衡状态随即遭到破坏,边坡内部的孔隙水压力也同时调整到暂态平衡的状态。在上游水位降落的过程中,这种流场的变化过程是不间断进行的。
水位降落后,首先是上游坡面附近的流场保持着较高水头,依然向下游方向流动。水位持续降落时,上游边坡内部的孔隙水压力无法及时消散,内部孔隙水压力高于边坡坡面附近的水压力,此时,边坡内部的地下水在压力差的驱动下开始向上游坡面方向流动,从而在边坡内部会出现自由面的最高点以及以最高点为中心的凸形分水岭。自由面形成分水岭以后,上游侧出现向坡面方向的渗流。分水岭的下游侧,地下水仍保持向下游坡面流动的过程。上游水位持续跌落时,边坡内孔隙水压力与上游坡面处的压力差也不断增大,边坡内分水岭的位置向边坡中央偏移,同时分水岭的凸形加剧。
图4是水位降落时细砂模型坝中一组自由面对应于降落时刻的变化情况。水位降速v=0.033 8 cm/s,k=1.7×10-2cm/s,μ=0.156,m=1.5,k/μv=0.017,结合自由面的渐变过程,可以判定本组试验结果应属于快降情况。图5是t=1 440 s时边坡内部的渗流场分布。
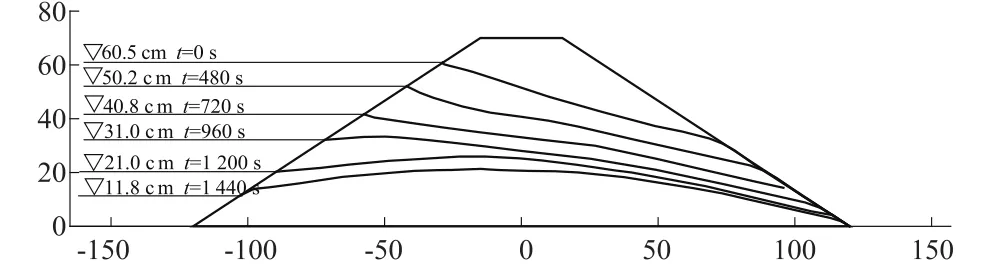
图4 砂土边坡中非稳定渗流瞬时自由面(单位:cm)Fig.4 Transient saturated surfaces of the sand box in sand

图5 t=1 440 s实测渗流场分布(单位:cm)Fig.5 Seepage field of the sandbox
黏土边坡中更容易形成骤降,上游水位骤降时边坡内部的水头消散滞后于坡前水位,迅速形成向上游坡面方向的渗流,如图6所示。
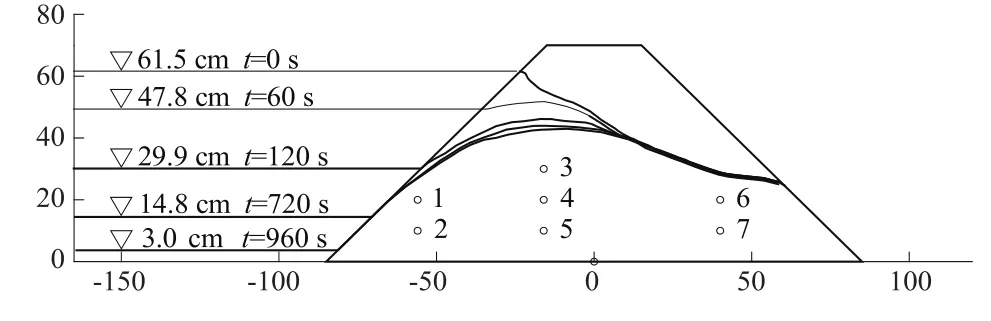
图6 黏土边坡中非稳定渗流瞬时自由面 (单位:cm)Fig.6 Transient saturated surfaces of the sand box in clay
水位急降过程中水位持续降落的后期,孔隙水压力滞后于坡前水位的现象愈来愈明显,形成的凸形自由面形状也突出。此时的自由面最高点附近孔隙水压力大于周围部位,渗流方向是同时往下游和上游边坡的。
3.2 水压力分布规律
边坡上下游水压力值在非稳定渗流过程中变化幅度不同,上游边坡的水压力值在非稳定渗流过程中的减幅较边坡内部和下游边坡内水压力值的变化大。如图7,黏土上游边坡附近的位置1和2的水压力减幅分别为5.14%和6.25%。而边坡中部降幅为3.13%,下游边坡水压力值基本没有变化。
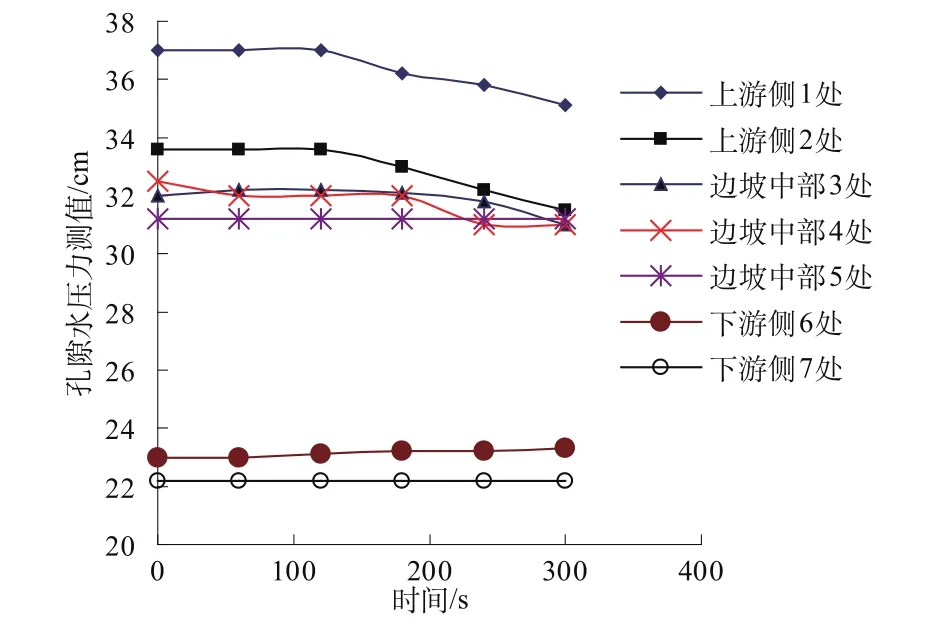
图7 非稳定渗流过程中孔隙水压力值对外水位的响应Fig.7 Response of pore pressure to external water level during unsteady seepage
黏土边坡水位骤降初期自由面下降幅度比后期幅度大,是由于边坡顶部宽度小,孔隙水压力的消散快,并且孔隙水压力的高值在坡面附近,而后期的孔隙水压力的高值逐渐向边坡内部发展。
3.3 渗透坡降分布规律
水位降落过程中下游边坡渗透坡降值逐渐减小。上游坡面附近渗透坡降值在坝内渗流向上游流动后从0开始逐渐增大,细砂坝工况中最终为0.2。但上游坡的坡降值最大处在水位附近,而非坡脚。
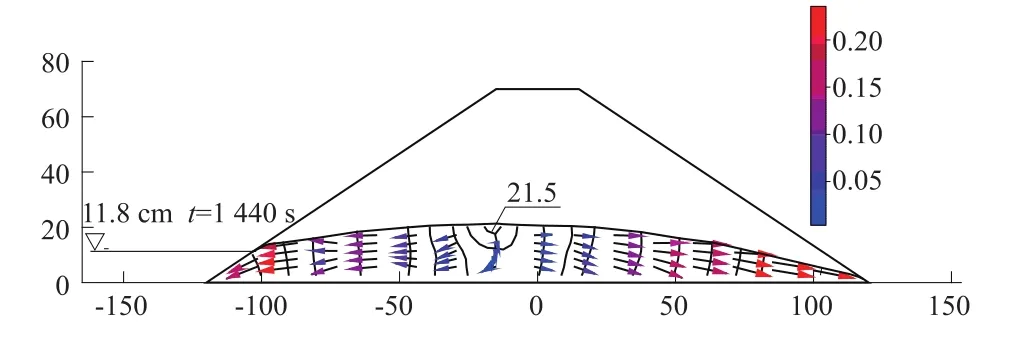
图8 瞬时实测渗透坡降值分布(单位:cm)Fig.8 Distribution of the seepage gradient
3.4 水位降落速度分析
由黏土和砂土材料坝的非稳定渗流场分布可知,水位降速为缓降时,边坡内孔隙水压力可在水位降落过程中完全消散,反映在浸润线与相应时刻的稳定渗流浸润线无异;而水位为快降和骤降时,边坡内孔隙水压力无法排出或无法完全排出,滞留在边坡内部的孔隙水压力势必改变渗流场形态,呈现出浸润线出现具有最高点和分水岭。
图9是黏土边坡中不同降速时上游边坡底部坐标为(-60,10)处测压管水位值的过程线。水位降速小时坡内可消散更多的水压力,降速最小(0.006 2 cm/s)工况测压管水压力消散了48.72%,而降速最快 (0.198 3 cm/s)工况仅仅消散了0.25%,差值达到了48.46%。

图9 不同降速的测压管水位过程线Fig.9 Piezometric levels in unsteady seepage
骤降和快降时坝内渗流方向也与缓降时有所不同,试验结果表明,一旦出现最高点和分水岭,就会同时出现向上游坡面方向的渗流,而缓降中,水流始终是从上游向下游方向运动的。
从浸润线的变化规律来看,每个时段出逸点处的浸润线,随着水位降落,有从缓到陡的趋势。这也说明了出逸点处的渗透坡降有增大的趋势,且随着降落速度变快更加明显。
水位降落速度不同时,出逸点位置也不尽相同;同一工况的试验组次中,出逸位置在水位降落过程中是持续下降的;不同工况的试验组次,降落速度越快,出逸点位置越高。
4 非稳定渗流作用因素分析及浸润线简化计算
填筑材料对非稳定渗流的影响主要体现在渗流参数k和μ上,而上游水位的降落速度v是决定非稳定渗流分布及危害的主要判别指标。非稳定渗流流场在水位降落过程中不断调整,调整后瞬时自由面的形状是判别非稳定渗流流态的主要依据。k/μv影响着孔隙水压力的消散程度,表2表明k/μv越大,则消散率越高。

表2 不同的k/μv对边坡内部地下水消散的影响程度Table 2 The effect of index k/μv on pore water dissipation
毛昶熙等曾提出,k/μv为定值时,“土体孔隙中质点的降落速度与库水位降速存在比值关系”[1]。
按照流网计算渗流自由面在时段Δt内沿流线方向的移动距离应与孔隙水流速v'=v/μ有关,即l=(v/μ)Δt=(Δt/μ)k(Δt/Δl),又因时间与库水位降速和降距有关,故有

式中:l为沿流线移动距离;Δt为时间间隔;t为库水位降落总时间;H为水位降落总高度;Δh为Δt时间段内水位降落高度;Δl为Δt时间段内沿流线移动距离。
根据上式可知,当k/μv→0时,边坡内自由面在库水位下降过程中几乎不变,为骤降;当k/μv→∞时,自由面下降速度几乎与外水位同步下降,接近于稳定渗流,为缓降。国内外一般根据试验确定k/μv影响非稳定渗流的程度,其中k/μv<1/10按骤降考虑,此时,边坡内部渗流自由面在库水位降落后仍保持有总水头的90%左右,故可近似认为自由面没有下降;k/μv>60按缓降考虑,水位下降很慢,边坡内部自由面只保持总水头的10%,不致影响边坡稳定性;k/μv>100时,自由面与外水位基本上同步下降,可视为稳定渗流。
骤降、急降及缓降过程中非稳定自由面形状变化形式是不同的。急降时靠近坡面处的渗流能及时消散,分水岭是向边坡内部偏移的;而骤降时,边坡内部的水无法及时排出,分水岭在边坡坡面附近快速形成,随着水位下降,分水岭是有向坡面方向偏移的趋势;缓降,则不会出现分水岭。
水位降落过程中,确定浸润线最高点是直观判断非稳定渗流对边坡安全危害的关键。根据最高点位置即可利用分段法对上下游浸润线分别求解。
毛昶熙等人[1]根据一系列的工程实例和试验结果,总结了以渗流自由面最高点位置判断非稳定渗流的经验公式:

式中:H为下降水位;T为水位降落的总时间;t为水位降落过程中瞬时时刻的累计降落时间,t≤T;α为经验系数,α=0.31。
根据试验结果发现公式(2)中α=0.31的经验系数在验算缓降时,与试验结果能够较好吻合,但对骤降的情况,与试验有一定的差别。本次试验有缓降、急降和骤降等情况,可根据试验与计算结果中浸润线最高点位置,分析总结与各参数之间的关系。图10为非稳定渗流浸润线最高点计算示意图。

图10 非稳定渗流浸润线最高点计算示意图Fig.10 Calculation schematic diagram of the peak on prelatic line in transient seepage
图11 是一组不同降速下的浸润线最高点的轨迹。可见,浸润线最高点都是向边坡的中部移动。降速越慢,最高点出现的时间越晚,出现最高点的初始位置也较低。

图11 最高点位置轨迹图Fig.11 Paths of the peak on phreatic line
图12 所示的结果表明,h0/H与 t/T之间存在较为明显的线性关系,由试验结果,可进一步确定h0/H与 t/T以及参数 k/μv之间的关系。
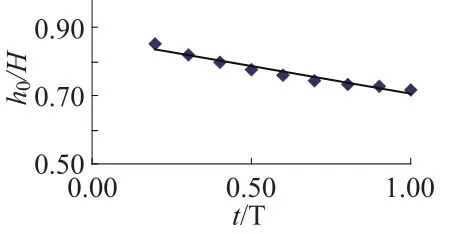
图 12 h0/H与 t/T间存在线性关系Fig.12 Linear relationship between h0/H and t/T
由于 h0/H与 t/T存在线性关系,则(1-h0/H)与(k/μv)0.25(t/T)间的关系也是线性的,根据试验中各时刻的数据作回归分析,可以得到两者间数值上的关系。
令 β=α(k/μv)1/4,据试验结果计算出各组k/μv对应工况时的β,拟合出曲线的α值,如图13所示。

图13 渗流自由面最高点经验公式的验证和扩展Fig.13 Empirical formula for estimating the peak on phreatic line
对骤降(k/μv=0.023和0.073)和部分急降(k/μv=0.125,0.73,1.509,1.581和3.163),α接近于0.60。
而当 k/μv值继续增大(k/μv=1.744,7.842,9.053,9.498和20.018),α接近于0.45。
对于缓降(k/μv=75.442,72.668和63.258)时,α值0.31与最高点的轨迹能够较好吻合。
因此公式(2)中的参数α可以表示为
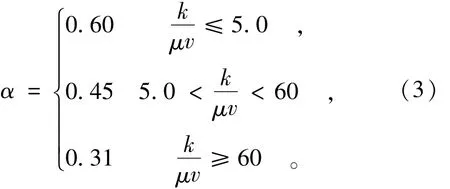
同时,可以解释为,对于骤降情况(k/μv<0.1)和缓降,可以分别使用α=0.60和0.31代入公式求解自由面最高点位置;对于水位急降情况,根据退水指标 k/μv的大小决定 α值,对于 k/μv≤5.0的急降,用α=0.60,对于5.0<k/μv<60的急降,用 α=0.45代入公式(2)即可计算出对应时刻或对应水位的浸润线最高点。
对于最高点的水平位置的计算,可以参考经验公式[7]计算

式中:ΔH为初始时刻上下游水位差;v为降落速度;t为水位降落过程中瞬时时刻的累计降落时间,t≤T;l为土坝上游坡脚距坝轴线的水平距离。
根据公式(2)、(3)和(4)可计算出某一时刻浸润线最高点的具体位置,再根据规范中的均质土坝分段法可分别计算出上下游侧浸润线的位置。此法可以初步估算非稳定渗流瞬时浸润线的位置。
5 结 论
(1)水位降落时非稳定渗流场复杂多变。一般根据自由面的形状分为骤降、急降和缓降。水位缓降时,边坡内部的自由面与稳定渗流差异不大,渗流方向始终是自上而下的;水位骤降和急降,边坡内孔隙水压力消散速率滞后于库水位的降落速度,在上游边坡附近形成凸形分水岭,分水岭上游侧渗流是向上游边坡方向,分水岭下游侧的渗流方向是向下游侧的。同时,在水位降落过程中,分水岭逐渐向边坡中央移动。
(2)边坡内部的孔隙水压力值在水位下降过程中变化不同,上游边坡水压力值的减幅较边坡内部和下游边坡内的水压力值变化大。
(3)在水位降落过程中,下游边坡渗透坡降逐渐减小,上游坡面附近的出逸坡降在地下水向上游开始回流后从0开始逐渐增大。同时,上游坡的坡降值最大处是在水位附近的,不是在坡脚。
(4)退水指标k/μv是影响流态的决定因素。其中,渗透性和给水度小的土质边坡内的渗流场的孔隙水压力消散速度远远小于渗透性较大的砂砾边坡,最易形成具有凸形分水岭的自由面;降落速度是决定非稳定渗流场特征的最关键因素,降速快的非稳定渗流上游边坡的孔隙水压力难以消散,上游边坡中的渗透坡降随着水位的降落逐渐增大,降速越大,坡降也越大。因此,k/μv是判断骤降、急降和缓降的依据,是考察边坡内部水头消散率的评价指标。k/μv越小,水头越难以消散,增大边坡内外的水头差,形成向上游坡面方向的渗流,且在上游边坡附近产生较大的渗透坡降。
(5)水位降落过程中,浸润线最高点高度与坡前水深的比值h0/H与降落时间t/T存在线性关系,同时,(1-h0/H)与(k/μv)0.25(t/T)间的关系也是线性的。根据试验结果拟合两者间的系数关系,得出了 k/μv不同区间时(k/μv)0.25前的系数 α值,可供设计中初步计算浸润线位置。试验结果还有待更多实际工程检验。
[1] 毛昶熙.渗流计算与分析控制[M].北京:中国水利水电出版社,2003.
[2] GUNTHER A.Dichtungen und Filterschichten[J].Was-serwirtschaft,1972,(7)
[3] 严 飞,詹美礼,速宝玉.堤坝非饱和渗流模型试验[J].岩土工程学报,2004,26(2):296-298.
[4] 余湘娟,王路军,张幸农.堤岸退水速度判别指标的试验研究[J].水利学报,2005,36(8):919-923.
[5] 毛昶熙,段祥宝,蔡金傍.北江大堤典型堤段管涌试验研究与分析[J].水利学报,2005,36(7):818-824.
[6] 朱 伟,山村和也.雨水、洪水渗透时河堤的稳定性[J].岩土工程学报,1999,21(4):414-419.
[7] 刘 洁,沙金煊.摄动方法求解水库水位下降时土坝中浸润线的位置[J].水利水运工程学报,1992,(1):65-72.
[8] 谢罗峰.渗流作用下边坡稳定性研究[D].南京:南京水利科学研究院,2009.

