体验生活中的不确定现象
倪敬标 张同军
生活中的事件可分成确定事件和不确定事件两种,本文从生活中的不确定事件谈起,让同学们领悟数学的魅力.
一、不确定事件发生的可能性大小(成功率)
例1将一枚硬币的一面贴上号码1,另一面贴上号码2,掷硬币两次,观察掷出的两个号码的积,下表是对200次实验数据整理的结果.

(1)用计算器计算频数,并填表;
(2)根据表中数据绘制折线统计图;
(3)当实验次数较少时,频率有什么特征?当实验次数增加时,频率有什么样的变化趋势?
(4)根据频率估计出现“积是2”的机会的大小.
分析:本题是一道频率计算问题,通过计算实验频率的大小,来探究实验的次数增加时频率与机会大小之间的关系.
解:(1)如下表.

(2)如图1.
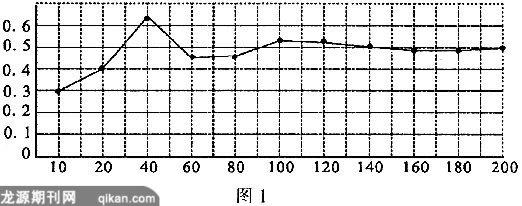
(3)当实验次数较少时,频率不稳定,波动较大;当实验次数增加时,频率波动变小,逐渐稳定在0.50附近.
(4)根据实验频率可以估计出现“积是2”的机会大小为0.50.
二、游戏的公平性
主要通过给出一些游戏,通过判断游戏双方获胜的成功率的大小是否相同,来确定游戏的公平性.常用的解题方法有两种情况:一是简单的游戏,可以通过分析的方法判断游戏双方获胜的机会的大小,根据机会的大小来确定游戏是否公平;二是比较复杂的游戏,可以通过多次实验的方法得到数据,计算不同实验次数下的频率大小,绘制频率折线统计图,通过观察,分析频率的稳定值,用稳定的频率值来估计机会的大小,进而确定游戏是否公平.
例2小华和小明玩一个游戏:一个盒子里装有四个完全一样的小球,小球上分别写着1,2,3,4四个整数,任意从盒子中摸出一个小球,小球上的数是几就再加上几,若得奇数小华赢,若得偶数小明赢.请你判断一下这个游戏对双方是否公平.
解析:要看这个游戏对双方是否公平,则需要看他们获胜的机会的大小是否一样.
若摸出的球上的数字是1,则1+1=2,2是偶数,若摸出球上的数字是3,则3+3=6,6是偶数,若摸出球上的数是2或4,则2+2=4,4+4=8,所以最后的结果都是偶数.这样小华赢的机会是0,而小明赢的机会是100%,所以游戏对双方是不公平的.
练习题:
1.一个口袋中装有4支红蜡笔、3支黄蜡笔、2支蓝蜡笔、1支绿蜡笔.从中任取一支,得到哪种蜡笔的可能性较大?
2.如图2所示,准备了三张大小相同的纸片,其中两张纸片上各画一个半径相等的半圆,另一张纸片上画一个正方形.将这三张纸片放在一个盒子里摇匀,随机抽取两张纸片,若可以拼成一个圆形(取出的两张纸片都画有半圆形),则甲方赢;若可以拼成一个蘑菇形(取出的一张纸片画有半圆、一张纸片画有正方形),则乙方赢.你认为这个游戏对双方是公平的吗?若不是,有利于谁?
参考答案:
1.因为红、黄、蓝、绿四种蜡笔分别占蜡笔总数的4/10,3/10,2/10,1/10,显然得到红蜡笔的可能性要比得到其他颜色蜡笔的可能性大.
2.这个游戏是不公平的.不妨设这两个半圆为A1,A2,正方形纸片为B,按照这个游戏规则,抽取纸片时可能出现的结果为:A1,B;A2,B;A1,A2.由此可知按此规则乙赢的可能性大.因此是不公平的.

