揭秘生活中的轴对称

陈　冬

轴对称是我们日常生活中经常能看到的现象，又是数学中常用的图形变换的一种，它是学习平移和旋转的基础.本文撷取生活中的轴对称问题，为各位同学展示其中的道理.

一、台球中的轴对称

例1如图1，EFGH为矩形台球桌面，现有一白球A和一彩球B.应怎样击打白球A，才能使白球A碰撞台边EF，反弹后能击中彩球B？

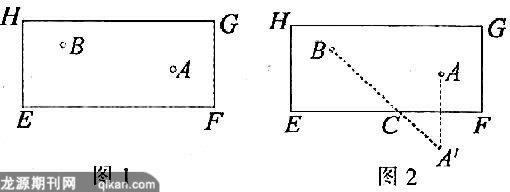
揭秘：我们常常看到世界斯诺克台球高手漂亮、准确的击球，无不令人赞叹.那应怎样解决这个问题呢？其实通过作点A关于EF的对称点A′，连接A′B，A′B与EF的交点C即为所求，如图2.这其中就是利用了轴对称的性质.

二、设计构成轴对称图形

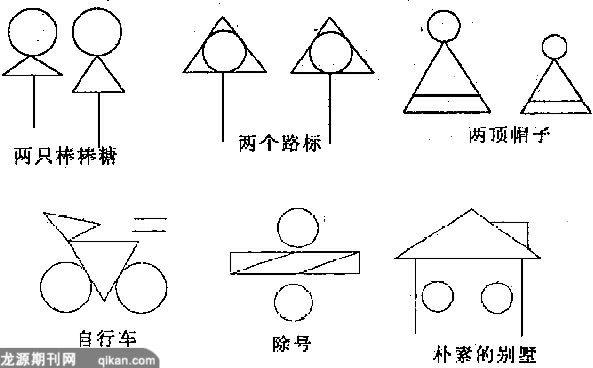
例2以给定的图形“○○、△△、=”（两个圆、两个三角形、两条平行线段）为构件，构思独特且有意义的图形.举例：如图3，左框中是符合要求的一个图形，你还能构思出其他的图形吗？请在右框中画出与之不同的一个图形，并写出一两句贴切、诙谐的解说词.

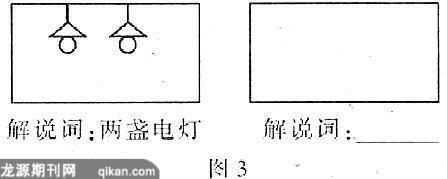
揭秘：由于此题没有标准答案，还因为一些固定思维方法，认为这样的题目既不考查计算又不考查证明，因此将此题忽略.实质上它是一道求符合已知图形条件的图形发散的应用题，因为结果是发散的，因而给同学们的思维提供了广阔的想象空间，同学们可以从多角度、多层次挖掘生活中、学习过程中及视觉之下的一切，将它们转化或设计为美妙的图形，同时它可以让同学们的思维插上想象的翅膀，在创造发散与转化发散的思维的天空中翱翔.解答如图4.

三、平面镜成轴对称

例32003年9月1日，小明拿起一盒牛奶刚要喝，妈妈说：“儿子，牛奶保质期过了，别喝了.”小明从镜子里看到保质期的数字是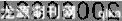，牛奶真的过期了吗？为什么？

揭秘：物体在镜子里的图象关于镜面成轴对称，镜子改变了物体的左右方向.一行数字中不仅每个数字被镜子改变左右结构，而且整行数字的左右顺序也被改变.因此，小明从镜子里看到保质期的数字是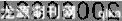，其实应该是20030824，而今天是2003年9月1日，通过比较发现牛奶保质期过了.

四、图形中的轴对称

例4请在下面这一组图形符号(如图5）中找出它们所蕴含的内在规律，然后在那根横线上空白处填上恰当的图.

揭秘：仔细观察这一组图形符号所蕴含的内在规律，我们发现它们分别是由正反数字1~7拼成的轴对称图形.这个趣例说明学习中需要细致观察，需要对数字、图形有一种敏感，也需要想象.本题的正确答案是.

五、游戏中的轴对称

例5图6是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子.我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿着棋子对称跳行，跳行一次称为一步.已知点A为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为.

揭秘：跳棋属于儿童游戏，成年人很少玩.根据约定的游戏规则，隔着一个棋子可沿直线对称跳行.棋子A若利用左边的一个棋子跳行，要跳4步才能进入对方区域；若利用右边的一个棋子跳行前进，跳3步就能进行对方区域.本题把数学轴对称知识和跳棋规则相连，体现了生活中处处有数学的道理.该题能开发学生的智力，让学生在玩中也能学到知识.

练习：

1.如图7是一个经过改造的台球桌面示意图，图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出（球可以经过多次反射），那么该球最后将落入的球袋是（）.

A.1号袋B.2号袋 C.3号袋D.4号袋

2.小强站在镜子前看见镜子里的墙上电子挂钟的读数如图8所示，此时实际的读数是多少？

3.下列图案是几种名车的标志，请你指出，在这几个图案中是轴对称图形的共有（）.

A.4个 B.5个C.6个 D.7个

4.如图9所示，要在街道旁修建一个牛奶站，向居民区A、B提供牛奶，牛奶站应建在什么地方，才能使A、B到它的距离之和最短？

5.数的计算中有一些有趣的对称形式，如：12×231=132×21；仿照上面的形式填空，并判断等式是否成立：

（1）12×462=________（）；（2）18×891=________（ ）.

参考答案：

1.B2.12：503.C4.略.5.264×21成立198×81成立