怎样开展探究式学习
胡红玲
教育心理学认为,学生数学学习的特点是“接受——建构”式的.它是学生在教师启迪诱引下,接受前人已有数学知识的过程.然而,在这个过程中,必须有学生积极主动的建构活动.因此,在新的教育理念指引下,寻找教师对学生数学学习的指导与学生自主探究式学习的平衡,即师生共同探究数学问题,培养学生创新能力,是搞好数学教学的关键问题.
一、向学生展示知识的形成过程,开展探究性学习
正确认识淡化概念教学理念.坚定确认数学概念(定义、定理、性质、公式、法则)是解决数学问题的起点,从知识发生的过程设计问题,突出概念的形成过程,是课堂教学开展探究性学习的广阔领域.
例如,《三角形内角和》关于多边形内角和教学中,我为同学们设计了如下开放性问题,让学生自己通过类比、归纳、猜想、探索公式.
同学们已经知道,三角形内角和等于180°(通过把△ABC的三个内角剪开,然后把它们的顶点A、B、C重合在同一点O,拼成一个平角),四边形的内角和等于360°.通过事先准备好只有一边相等的两个三角形,将相等的边拼在一起得到一个四边形,反过来,同学们清醒地认识到,这个重合的边正是四边形的对角线,将一个四边形分割成两个三角形.
通过表格,让学生归纳出n边形内角和定理的表达式.

学生顺利地完成上表,归纳得到n边形的内角和公式,接着我又提问:你能证明这个结论吗?
课堂上给学生足够时间,让学生观察、讨论.此时,有同学很快想到对角线,将多边形分割成若干个三角形,接着我请同学们动手画图.同学们通过讨论,作出了几种不同割法,富有创造性.学生通过类比,由特殊到一般,归纳猜想,得出公式:n边形内角和=(n-2)×180°(n≥3).
此时,看着同学们用不同割法得以证明,同学们一张张激动、兴奋的面孔呈现在我眼前.我把握时机,向同学们介绍了观察、类比、转化、归纳、猜想等方法在解题中的重要作用.
二、利用例题开展探究性学习
课本例题的结论,反映相关的数学理论本质属性,蕴涵着丰富的数学思想方法和精髓,是学生创造性思维的生长点,教学中对课本例题结论进行引申、拓展,是课堂教学开展探究性学习的重要手段.
已知:如图1,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
学生已有证明平行四边形和三角形中线定理的知识、经验,如何利用自己已有的知识来解决问题是认知上的难点,所以,我组织学生通过观察、讨论、交流,让学生在交流过程中产生顿悟.连接AC或BD构造三角形是解决此问题的关键.问题的解决由学生自己尝试,并在教师的帮助下加以完善.
在学生掌握解题的基础上,我又设计如下问题:
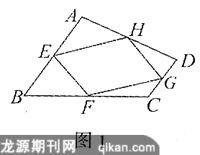
(1)当图1中的对角线AC=BD时,得到的四边形EFGH是什么四边形?
(2)当图1中的对角线AC⊥BD时,得到的四边形EFGH是什么四边形?
(3)当图1中的对角线AC=BD且AC⊥BD时,得到的四边形EFGH是什么四边形?
课堂上让同学们分组讨论,动手画图.同学们在讨论中发现:当对角线AC=BD时,对平行四边形EFGH来说,又有一组邻边相等,所以此时四边形是菱形.
随着问题(1)的解决,对问题(2)又展开了热烈讨论,当对角线AC⊥BD时,四边形EFGH是矩形.由(1)、(2)两个问题的解决,不难得出:既是菱形又是矩形的四边形一定是正方形,从而顺利地解决了问题(3).通过这三个问题的解决,进一步拓宽了学生的解题思路,完善了学生的认知结构,同时也让学生体会到了矛盾的普遍性存在于矛盾特殊性之中的辩证唯物主义观点.
此外,在教学中利用变式训练——拓展的方法,不仅适用于几何问题,更适用于代数问题等.勾股定理的证明不是发现了几百种证法吗?这就是最好的例证.
在实际教学过程中,学生通过师生共同探究,不仅体验了成功的喜悦,还能感受到学习数学的乐趣,从而形成了对数学学习的积极情感和态度.
实践证明,深化教育改革,关键在课堂.然而,潜移默化地培养学生的探究习惯是不可缺少的途径.
三、创设实际应用问题的情境,开展探究性学习
数学来源于生活,运用数学知识解决问题是数学学习的归宿.根据教学内容,设计应用问题是课堂教学开展探究性学习的好素材.例略.
综上所述,探究是数学的生命线.师生在数学活动中都应该具有不畏艰险、知难而进的精神,还要具有顽强的意志品质.形成探究知识,培养探究习惯,进而使学生获得知识的同时,在思维能力、情感态度及人文观、价值观等多方面得到进步和发展.

