用Ｆｌａｓｈ ＭＸ动态显示“牛顿草图”

朱龙青

在高山上用不同的水平初速度抛出物体。若初速度一次比一次大，物体落地点就一次比一次远；当初速度足够大时，物体就再也不落回地面，而是做以地心为一个焦点的不同轨道的椭圆（或圆）运动。当物体向近地点（或远地点）运动时，物体的速度将变大（或变小）。用Flash MX动态显示上述“牛顿草图”时，可以在动态文本框中呈现不同时刻物体的速度变化。

本课件有助于学生形象而直观地领悟牛顿有关人造天体的科学设想，理解开普勒定律以及人造卫星原理（图1）。

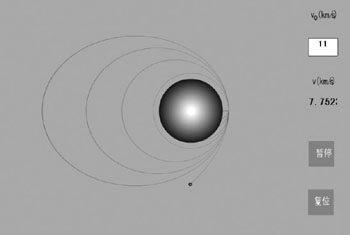
一、布置舞台

运行Flash MX新建文档，将文档属性设定为宽550像素、高450像素，帧速40帧/秒，背景为灰色。

二、建立库物件

打开库，新建一个名为dq的电影剪辑（图2），利用绘图工具绘制一个灰白辐射色的球代表“地球”。打开信息面板设定“地球”的半径为54像素（图3），以便显示及编程。

新建一个名为wx的电影剪辑，利用绘图工具绘制一个红辐射色的球代表“卫星”，打开信息面板设定“卫星”的半径为6像素。

新建一个名为di 的电影剪辑，利用绘图工具绘制一个蓝色的圆代表轨迹“点”（通过复制轨迹“点”描绘“卫星”的运动轨迹），打开信息面板设定轨迹“点”的半径为1像素。

新建一个按钮，取名为Button，利用绘图工具在其第一帧绘制一个红色正方形（其边长为43像素），并在第四帧插入一个帧，完成按钮制作。到此完成所有库物件的制作。

三、组织场景

回到场景，在时间线上（从下到上）共建七层（图4），分别将各层命名为“地球”、“卫星”、“点”、“开始暂停”、“复位”、“文本”、“actoin”。

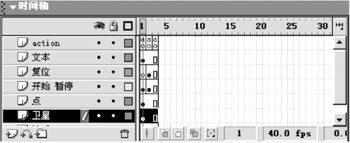
单击“地球” 层的第一帧后，把库中的“dq”拖到场景中。打开信息面板，将地心的坐标设为（300，220）；单击“卫星”层的第一帧后，把库中的“wx”拖到场景中,将“卫星”的坐标设为（364，220）；单击“点”层的第一帧后，把库中的“di”拖到场景中,把轨迹“点”的坐标设为（364，220）；单击“开始暂停”层的第一帧后，把库中的“button”拖到场景中右边的适当位置，并在此按钮的上方输入文字“开始”作为控制开始播放的按钮；在该层的第二帧插入一个关键帧，把库中的“button”拖到场景中“开始”按钮的上方适当位置，并在其上输入文字“暂停” 作为控制课件暂停播放的按钮；在复位层的第二帧插入一个关键帧，把库中的“button”拖到场景的右边“开始”按钮的同一位置上（这样使课件播放时只显示这两个按钮中的一个），并在其上输入文字“复位”作为控制课件回到原始状态。

单击“文本”层的第一帧后，利用文字工具绘制一个文本框（宽48像素，高30像素）放在舞台的右上角（“暂停”按钮的上方）适当位置，在此文本框的上方输入“v(km/s)”，制成一个用以显示卫星瞬时速度的动态文本框。同理，绘制一个同样的文本框放在上述文本框的上方，在此文本框的上方输入“vo(km/s)”，制成一个用键盘输入卫星水平初速度的输入文本框。

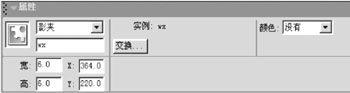
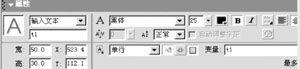
在场景中选中“卫星”后，打开属性面板，在实例名中输入字母wx（图5）；选中轨迹“点”后，在实例名中输入字母di；选中输入文本框后，把文本类型设定为输入文本，下方输入字母t1，并在变量名中也输入字母t1（图6）；选中动态文本框后，把文本类型设定为动态文本，下方输入字母t2，并在变量名中也输入字母t2。注意文本类型不能设定错，变量名也不能不输入，否则程序将不能传递变量。

四、编写脚本

（1）选中舞台上的“开始”按钮，单击动作面板写入代码：

on (release, keyPress "") {

if (t1<0) {

stop();

t1 = "";

t2 = "";

} else {

vo = t1/100;

gotoAndPlay(2);

}

}

//若输入速度小于0，不播放，否则按“开始”按钮，或Enter键，把输入的初速度赋予vo并跳转到第二帧播放

（2）单击“开始暂停”层的第二帧，选中舞台上的“暂停”按钮写入代码：

on (release) {

stop();

}

//按“暂停”按钮则停止播放

on (keyPress "") {

play();

}

//按“Enter”键则继续播放

（3）单击“复位”层的第二帧，选中舞台上的“复位”按钮写入代码：

on (press) {

gotoAndPlay(1);

}

//按“复位”按钮回到第一帧。

（4）action层的第一帧，写入代码：

stop();

fscommand("fullscreen", "true");

//命令全屏播放

t = 0;

//时间归0

j = 0;

//极角归0

t1 = "";

//输入速度归0

t2 = "";

//动态速度归0

r = 64;

//极径初始值（卫星距地心的初始距离）

setProperty("di", _x, 364);

setProperty("di", _y, 220);

//轨迹点的起始坐标

setProperty("wx", _x, 364);

setProperty("wx", _y, 220);

//卫星的起始坐标

（5）action层的第二帧插入一个关键帧，写入代码：

t = t+dt;

dt = 15;

//dt为运动时间的步长

n = n+1;

//轨迹点的个数自动增加

ro = 64;

//代表卫星的起始高度64百千米

h = ro*vo;

//卫星椭圆运动的角动量大小不变

p = h*h/d;

//卫星椭圆轨迹方程的半正焦弦

e = Math.pow((1+h*h/d/d*(vo*vo-2*d/ro)), 0.5);

//卫星椭圆轨迹方程中的离心率e(且0

d = 64*64*0.000098;

if (t1 == 0 && t<=452) {

setProperty("wx", _x, 300+ro-0.5*0.000098*t*t);

setProperty("wx", _y, 220);

//卫星自由下落动态坐标，t<=452表示落到地面以前运动

setProperty("di", _x, 300+ro-0.5*0.000098*t*t);

setProperty("di", _y, 220);

//轨迹点动态坐标

r = getProperty("wx", _x)-300;

t2 = 0.0098*t;

}

//在动态文本框显示卫星的瞬时速度（单位为千米/秒），若输入初速度vo=0，卫星在x方向位移x=0.5gt*t，共运动10千米，速度近似用v=gt计算，单位分别是千米、千米/秒

if (t1>0 && t1<=7.9 && r>=54) {

j = j+dt*h*Math.pow(r, -2);

//j为卫星椭圆运动的极角，由角动量守恒r*r*dj/dt=h得dj=dt*h/r*r

r = p/(1-e*Math.cos(j));

//卫星椭圆运动的极径。注意,随着初速的增大，相对于舞台的椭圆的右焦点逐渐向左移（左焦点即地心不动）t1=7.9时，左右焦点重合，t1>7.9后左右焦点将交换位置，理解这点很重要！

setProperty("wx", _x, 300+r*Math.cos(j));

setProperty("wx", _y, 220+r*Math.sin(j));

setProperty("di", _x, 300+r*Math.cos(j));

setProperty("di", _y, 220+r*Math.sin(j));

//输入速度小于第一宇宙速度时，卫星及轨迹点的动态x、y坐标， r>=54表示落到地面就停止运动

t2 = 100*Math.pow(vo*vo-2*d*(1/ro-1/r), 0.5);

}

//在动态文本框显示卫星的瞬时速度，单位为千米/秒

if (t1>7.9 && t1<=11.2) {

j = j+dt*h*Math.pow(r, -2);

r = p/(1+e*Math.cos(j));

//由于卫星的初速大于7.9千米/秒后，左右焦点已交换位置，为确保都过起点，式中e已改为-e

setProperty("wx", _x, 300+r*Math.cos(j));

setProperty("wx", _y, 220+r*Math.sin(j));

setProperty("di", _x, 300+r*Math.cos(j));

setProperty("di", _y, 220+r*Math.sin(j));

//输入速度大于第一宇宙速度小于第二宇宙速度下，卫星及轨迹点的动态x、y坐标

t2 = 100*Math.pow(vo*vo-2*d*(1/ro-1/r), 0.5);

}

if (n<=5000) {

duplicateMovieClip("di", "di"+n, n);

}

//轨迹点不能复制太多（限制在5000个以内）否则影响播放速度，当然也可以少点。

（6）action层的第三帧插入一个关键帧，写入代码：

gotoAndPlay(2);

//跳转到第一帧循环播放。

最后在各层（除action层之外）的第三帧分别插入一个插入帧，这样整个动画创建完毕。