小学数学作业靶向改进的实践路径

摘 要 数学作业已成为学生数学核心素养发展的重要生长点。然而，数学作业设计呈现“控时不控质”的低阶水平，存在作业设计主观化、作业题型无效化和作业模式固态化等问题。因此，可以通过靶向改进的数学作业重构化实践，精准研判学生问题认知，筛选与整合学生真实问题，以问题链为作业设计基础，建设能力共生的数学作业题型库，创造思维灵动的作业模式群，实现提纯知识、提升素养与提质增效的教学目标。

关" 键" 词 数学作业；靶向改进；问题链整合；题型库建设；模式群创造

引用格式 朱家浩.小学数学作业靶向改进的实践路径[J].教学与管理，2025（05）：57-60.

数学作业是学生数学核心素养发展的重要生长点[1]。然而，笔者对校内部分学生进行问卷与访谈的双重追踪调查，通过数据分析，发现数学作业设计呈现“控时不控质”的低阶水平。虽然教师自主设计作业的意识得到了增强，但未能改变机械化、大众化的作业模式，究其原因主要有三：一是作业设计主观化，忽视认识分析；二是作业题型无效化，忽视能力培养；三是作业模式固态化，忽视思维发展。因此，笔者积极探索小学数学作业改进路径，通过靶向改进的数学作业重构化实践，精准研判学生问题认知，筛选与整合学生真实问题，以问题链为作业设计基础，建设能力共生的数学作业题型库，创造思维灵动的作业模式群，实现提纯知识、提升素养与提质增效的教学目标。

一、三单研判：基于认知显现的问题链整合路径

问题是一切数学活动的基础，而数学作业靶向改进需勾连学生真实问题。因此，教师通过问卷调查单、课堂生成单、练习分析单的实施，使得学生暴露自身学习问题，通过对学生问题的全面收集与精准研判，将有价值的数学问题整合成问题链，从而确定数学作业的设计方向。

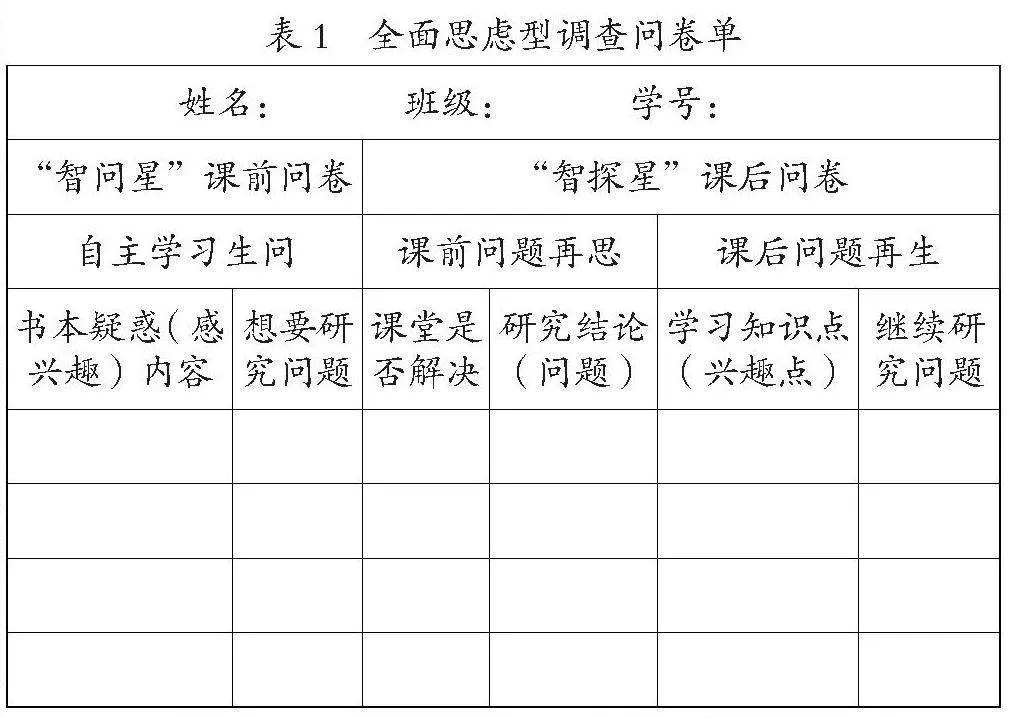
1.问卷调查单，全面思虑“显问”

问卷调查单用于收集学生学习前后所产生的问题，通过课前与课后调查问卷单的双重实施，引导学生自主呈现学习的认知问题。课前问卷单关注预习过程中有疑惑或感兴趣的问题，课后问卷单关注学生对知识存疑或衍生的问题（见表1）。

教师需全面收集、对比、思考与分析学生学习前后所产生的问题，筛选出对教学目标或学生能力有推进价值的问题，将其运用于数学作业的设计。

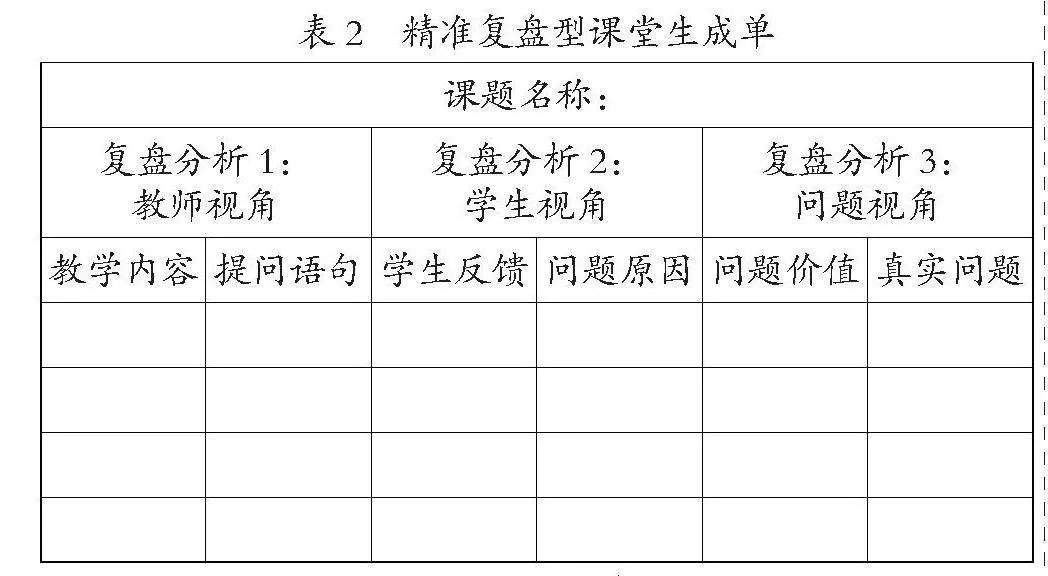
2.课堂生成单，精准复盘“现问”

课堂问题是重要的生成性资源[2]。虽然学生在错误表达后会经历讨论、辨析等过程，最终会生成正确表达，但学生的错误认知需要被收集与复盘。教师通过课堂生成单的及时记录，精准复盘课堂提问、反馈等教学环节，重点关注与分析核心问题的错误表达、一般问题的集中性错误表达以及学生困惑问题的本质，以此明确学生课堂生成的价值性问题（见表2）。

教师通过审视整节课的具体内容，抓住教学过程的卡壳点、疑难点与矛盾点，借助教师视角、学生视角、问题视角的联结性分析，深度复盘教师提问的语句、时机与方式，定性分析学生每条错误背后的原因，根据学生错误原因确定问题的价值大小，将价值性问题创编成学生的数学作业。

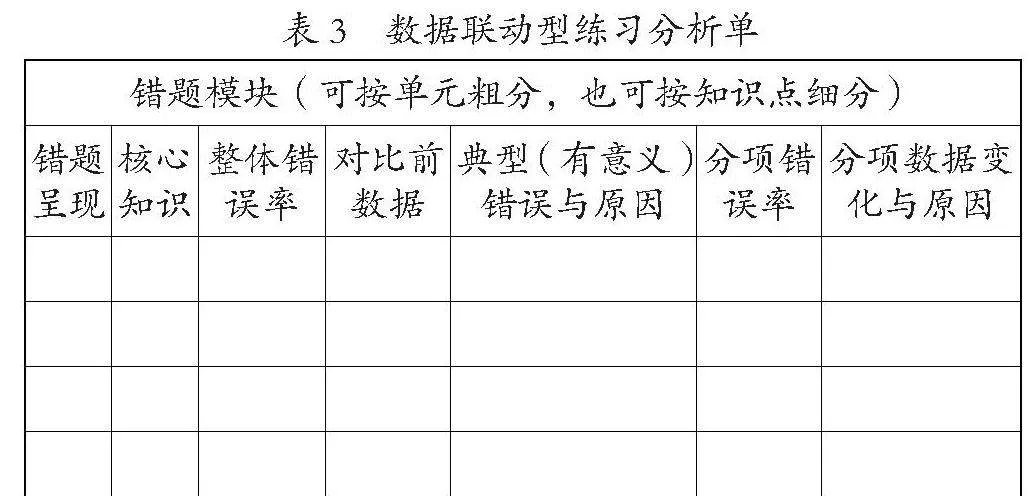
3.练习分析单，数据联动“锁问”

练习具有巩固数学知识的作用，亦是反映学生问题最为直接的方式。教师通过练习分析单收集与分析学生的错题，以模块化的方式记录学生的同类型知识问题，勾连练习中错题的核心知识点（见表3）。同时教师需计算整体与分项的学生错误率，对比同类型错题数据的前后变化，深度分析新增典型（有意义）错误以及分项数据变化的具体原因，进而联动数据变化，锁定学生的问题。

教师通过练习错题甄别学生错误的问题指向，确定核心知识点，并寻找与标记先前同类型错题出现的频率，通过整体数据与分项数据变化的双重对比，重点关注高占比数据、持续上升数据与新问题数据，全方位思考数据动态变化的深层次问题，在此基础上展开数学作业的针对性设计与实施。

二、五型重构：基于能力共生的题型库建设路径

学生数学能力不应是一元的独立发展，而应是多元的协同发展，这就需要全面评估与培育学生的数学能力。在设计数学作业时，教师以学生的真实问题为出发点，打破原有单一的题型局限，重构培育多种数学能力的数学题型库，帮助学生弥补数学能力上的发展短板，促使他们经历由低级到高级、由简单到复杂的能力培养过程。

1.“关联衍生”题型，促生理解能力

“关联衍生”题型重在沟通母题与子题的内部联系，既有巩固知识点的作用，又为学生思维发展提供题型支架。教师提炼与细化例题与“首见题”两类母题的错误问题点，重组问题点的错误信息，衍生出更具针对性的子题，引导学生在类情境子题、类方法子题的解决过程中，真正理解与积累母题经验，促使学生理解能力的生长。如根据母题“长方形菜地的周长是184m，长是宽的3倍。菜地的长、宽各是多少？”及学生的错误问题衍生出如下题型：

类情境子题：长方形菜地的周长是150m，长比宽多50%，菜地的面积是多少？

类方法子题：用240cm的铁丝围成一个长方体的容器，已知长方体长、宽与高的比是5：4：3，那么长、宽、高各是多少厘米？

从情境与方法的视角出发，构建适合学生能力发展的衍生型子题，既指向知识点的熟悉与巩固，更扩大了学生的认知视野，促使学生在解决与反思子题的过程中，明晰母题与子题间的关联作用，以此重构对母题的认知经验。

2.“问题说理”题型，促生思辨能力

“问题说理”题型重在学生的自我思辨，以文字、图表等表征问题解决的过程。教师着重研究学生同类知识的典型错误与高频错误，对错误问题开展比较分析，区分学生问题的原因类别，从而建构对话辨析题、观点补充题与结论证明题三大说理题型，促使学生自主经历说理、讨论活动的全过程，真正明晰数学问题本质，以此生成高阶思辨能力。如教学完比的知识后，教师设计如下题型：

小明说：“长方形长与宽的比是3：2”；小红说：“世界杯上，法国与英格兰的最终分数是3：2。”

问题：这里的“3：2”都是比，你同意吗？请说说你的理由。

此题通过对话的形式呈现问题情境，聚焦比认知上的易错点：只要是比的形式就一定是比。教师设计“问题说理”型数学题，让学生经历自我辨析的全过程，使学生明晰什么是比，真正理解比的意义。

3.“经验重塑”题型，促生探究能力

“经验重塑”题型重在重新塑造学生的认知经验，通过实践、讨论等探究活动破除错误经验，重建正确经验。教师聚焦并反思学生的概念性错误与生活性错误，挖掘错误经验中的价值性问题，寻找问题与探究方法间的契合点，从而设计成实验纠偏题、生活体验题与模拟参与题等数学题型。学生通过具身操作等探究过程精准纠偏，重塑全新的认知经验，培养学生的探究能力。如教学植树问题后，教师设计如下题型：

在50米长的马路一侧种树，相邻两棵树间隔5米（两端都不种）。

问题1：可以种几棵树？

问题2：小明认为可以种10棵树，你赞同小明的想法吗？说一说你的理由。

此题是植树问题“两端都不种”的情况，学生学习后的普遍认知是“棵树=间隔数-1”。然而在实际生活中还有很多不同的种法，比如第一棵树距离路的一端2米，学生通过模拟画图或实践的方式发现总共可种10棵树，这样的子题型是对学生认知的重塑与补充，可以更好地拓展学生的数学思维。

4.“学科融合”题型，促生内化能力

“学科融合”题型重在加强各学科间知识的联系与融合，使得作业题目既有浓厚的数学味，又有多元的学科痕迹[3]。教师将学生的数学问题尝试勾连一门或多门学科，探寻问题与学科属性间的联结点，定位作业题型的设计方向，以此定制出学科融合专项题型，引导学生深入参与问题的解决过程，促使他们正确灵活地提取与运用各学科知识点，实现学生对学科知识的内化。如教学完铺地砖问题后，教师设计如下跨学科学习题型：

跨学科学习的融合实践，让学生自主经历测量、计算与铺设等活动过程，真正理解“地砖小面积填充房间大面积”的平铺过程。同时融入美术学科的绘画与语文学科的撰文，促使学生用图表、文章等方式深入理解铺设原理、复盘铺设过程，以此内化铺地砖问题的核心知识。

5.“文化浸润”题型，促生创新能力

“文化浸润”题型重在强化学生对数学文化的理解，让学生生成必要的数学文化素养。教师通过梳理第三学段数学家、数学史、数学结论等数学文化知识，审视与提炼数学文化的教学与育人价值，创新地将其改进开发为“文化阅读题”“文化调查题”“文化设计题”等浸润式研究题型，引导学生参与数学文化的学习与讨论，促使学生生成创新能力。如教学完鸽巢问题后，教师设计如下题型：

同学们，老师相信你会解决鸽巢问题，但你知道鸽巢问题是谁发明的吗？为什么会有鸽巢问题？……一系列与解题无关的问题，其实更值得我们去研究与思考。请你以数学手账的形式自主研究与设计吧。

学生的学与教师的教往往止于重复式的解题，而忽略了知识点背后数学文化的追溯与思考。为此，教师设计了“文化调查题”，让学生自主经历鸽巢问题的资料查阅、故事梳理等过程，借助数学手账呈现自己对鸽巢问题的独特理解。最后，教师将学生的数学手账装订成册，以此实现知识的共享与互补。

三、三式升值：基于“思维灵动”的模式群创造路径

教师要学习作业设计与实施的先进理念，结合对教学疑难问题的分析，优化作业的内容与功能。然而不同的作业模式会使学生生成不同的思维体验，故教师以问题链为设计基础，结合题型库创造出优学、辅学、探学三式作业模式群，实现数学作业分层感悟、过程反思与项目辐射的系统性升值，发展学生数学思维的灵动性。

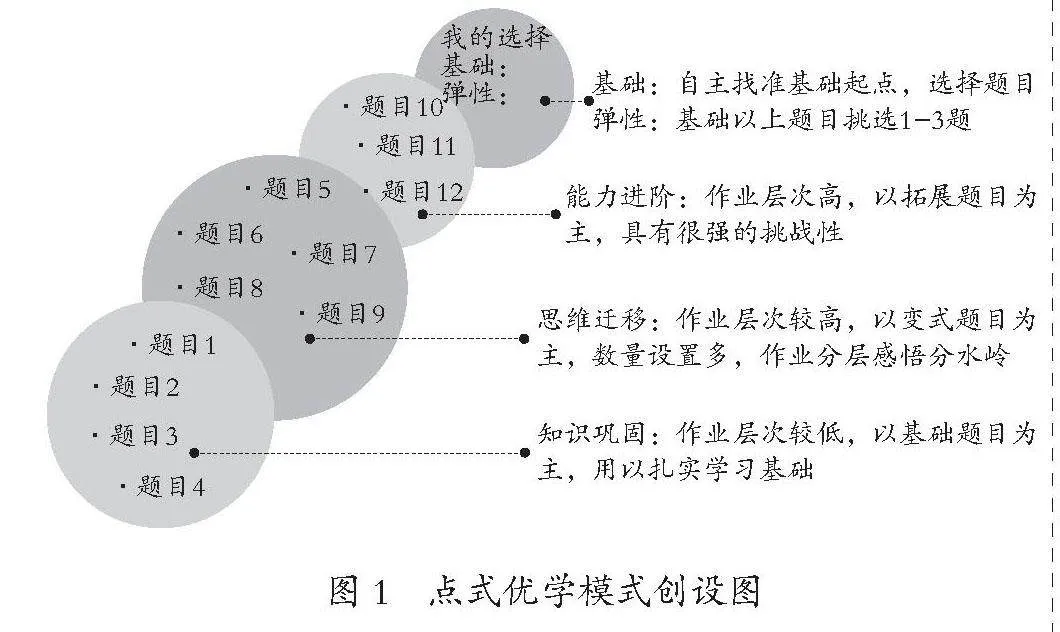
1.点式优学模式，实现分层感悟

点式优学模式是指在三个作业指向维度中分别设置多道题型，学生可根据自身数学能力自主搭配选择，体现分层作业对学生的优学价值。教师根据学生间数学能力的差异程度，创造知识巩固、思维迁移、能力进阶不同目标与难度指向的作业子题目群。同时，教师需引导学生全面分析自身能力，明晰自身认知与思维的起点，挑选匹配的“基础＋弹性”题目组，形成点式优学作业模式。

此作业模式在各维度中均设置了足够数量的题型，给予学生作业选择的自主性与分层性。这样的设计既分层巩固了数学知识点，又充分调动学生的积极性，激发学生的内在潜能。

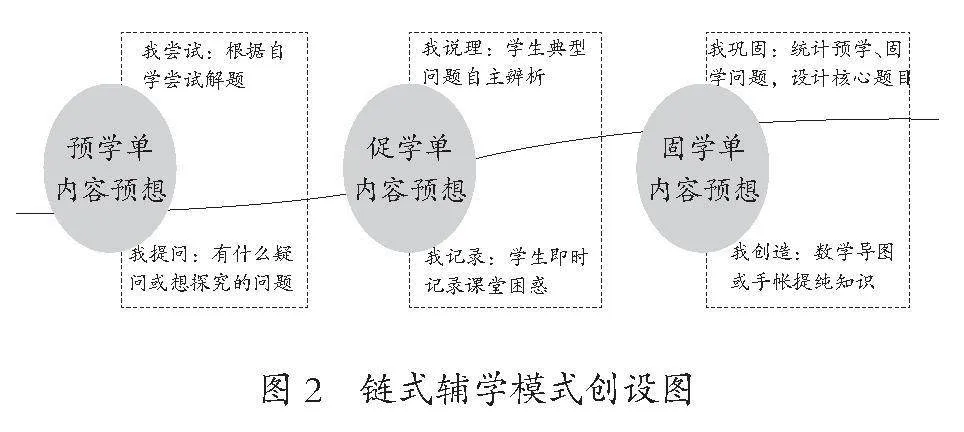
2.链式辅学模式，实现过程反思

链式辅学模式是指学生作业内容贯穿学习全过程，不断转变与巩固学生数学认知的作业模式。教师根据学习发生顺序，创造了预学单、促学单、固学单三张学习单[4]，内容设计既有核心问题的统一，也有自我学习问题的暴露，使得学生的学习循序渐进。为了展现学习单间的连续性与独特性，前面学习单的核心问题会在后续学习单中跟进解决与补充，这也拓宽了学生问题解决的途径，提升学生数学思维。

各学习单都设计两个内容模块：一是基础知识的学习、辨析与巩固；二是学习过程的问题呈现与知识反思。通过三单辅学作业模式的实施，让学生学习过程真实、有序发生，各阶段的学习程度可视化，更好地引导学生反思与调整，以此提升学生数学学习的深度、广度与温度。

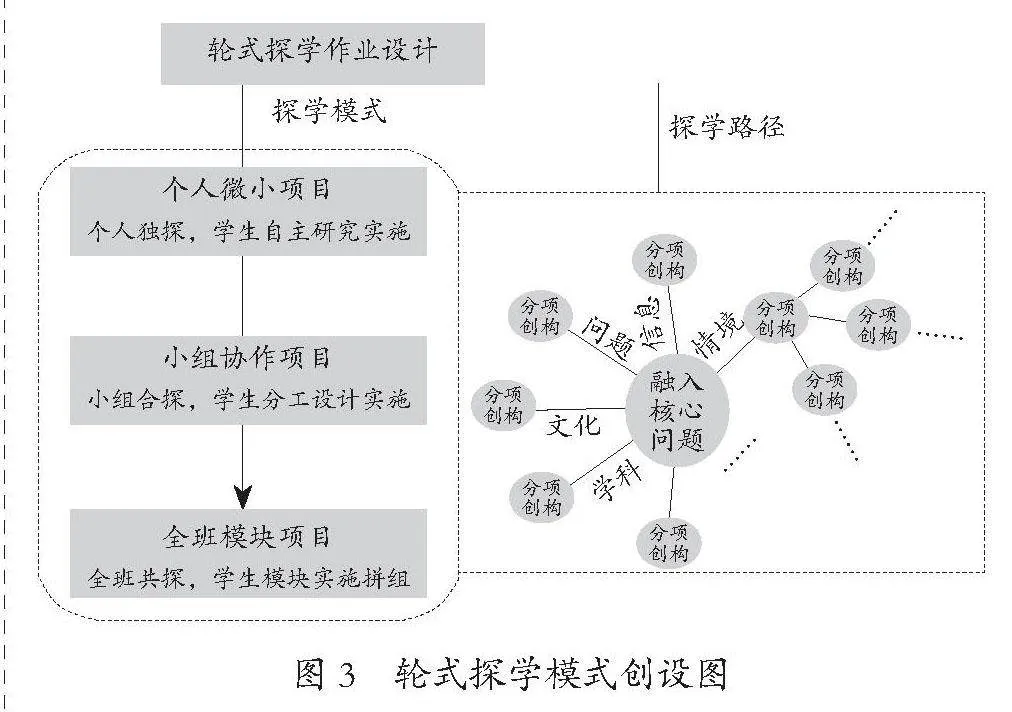
3.轮式探学模式，实现项目辐射

轮式探学模式是指以学生核心问题为圆心，增加情境、信息与问题等数学元素，重新架构与延伸问题点的作业模式。教师围绕问题本质，创造了“个人微小项目”“小组协作项目”“全班模块项目”三阶项目探学作业，通过驱动性问题衍生出不同指向的子问题群，引领学生开展主题化或项目化的数学探学活动，增强核心问题辐射作用，实现学生学习过程的共进与共生，提升学生思维品质。

教师可以根据核心问题的研究难度或价值，对标学生自身能力，开展适合的轮式探学作业模式。通过核心问题下子问题的创设，引导学生开展不同方向的探学研究。学生通过项目的研究与成果的整理汇报，促进数学思维的灵动发展。

总而言之，小学数学作业的改进不应是教师个人感觉的呈现，而是源于学生又用于学生的闭环式体现。因此，教师需要精准研判学生认知，立足学生的生成性问题，靶向改进数学作业，重构数学作业题型库，创造数学作业模式群，促进学生多元能力与灵动思维的协同发展，以此打造以问题链为导向的小学数学作业改进新路径。

参考文献

[1] 段艳蕊.以数学作业设计助力学生核心素养发展[J].江苏教育，2022（81）：74-75.

[2] 马鲁彦.小学数学课堂教学中错误资源的有效利用[C]//广东教育学会.广东教育学会2023年度学术讨论会论文集（十一）.山东省菏泽市牡丹区第二小学，2023：5.

[3] 李云凤.聚焦学科融合 优化小学数学作业设计[J].天津教育，2024（12）：16-18.

[4] 范林伟，杨雅军.小学数学手账的学理意蕴与实施策略[J].教学月刊·小学版（数学），2020（10）：7-9.

[责任编辑：陈国庆]