基于井下参数的SCNGO-SVM卡钻预警方法研究

针对卡钻风险预测的问题，提出了一种融合正余弦和折射反向学习的北方苍鹰优化算法（SCNGO）和支持向量机（SVM）的卡钻预警模型。针对北方苍鹰优化算法（NGO）容易陷入局部最优以及初始解的分布具有随机性和非均匀性的特性，引入折射反向学习策略初始化北方苍鹰算法个体、正余弦策略替换原始苍鹰算法的勘察阶段的位置更新公式和正余弦策略的步长搜索因子进行改进，将SCNGO用于SVM寻参，并将模型SCNGO-SVM应用于卡钻预警。研究结果表明：SCNGO在收敛速度、寻优精度等方面明显优于NGO、WOA（鲸鱼优化算法）及SSA（麻雀优化算法）；该卡钻预警模型对于卡钻的预测准确率高达97.33%，相较于WOA-SVM、NGO-SVM、SSA-SVM卡钻预警模型，在预测准确率和运算速度上均有较大的提升。该模型为卡钻的预测及其工程应用提供了理论指导。

卡钻预警模型；北方苍鹰优化算法；性能测试；折射反向学习策略；正余弦策略

TE28

A

DOI： 10.12473/CPM.202402007

Research on SCNGO-SVM Sticking Warning

Method Based on Downhole Parameters

Zhang Tao1，2，3" Xia Peng1，2，3" Li Jun4" Wang Biao4" Zhan Jiahao4

（1.Beijing Information Science amp; Technology University;2.Beijing Key Laboratory of High Dynamic Navigation Technology， Beijing Information Science amp; Technology University;3.Key Laboratory of Modern Measurement amp; Control Technology， Ministry of Education;4. College of Petroleum Engineering， China University of Petroleum （Beijing））

As to sticking risk prediction， a SCNGO-SVM sticking warning model was proposed. It integrates the sine cosine and refracted opposition-based learning Northern Goshawk Optimization （SCNGO） with support vector machine （SVM）. Considering that the Northern Goshawk Optimization （NGO） may fall into local optima and yield initial solutions in random and non-uniform distribution， the refracted opposition-based learning strategy was introduced to initialize the individuals of NGO. Meanwhile， the sine cosine strategy was introduced to replace the position update formula of NGO in the survey phase， and the step size search factor of the sine cosine strategy was used to improve the NGO， thus forming SCNGO. The SCNGO was used for parameter search of SVM. Finally， the SCNGO-SVM model was used to conduct sticking warning. The research results show that the SCNGO is obviously better than the NGO， whale optimization algorithm （WOA） and sparrow search algorithm （SSA） in terms of convergence rate and optimization accuracy. The SCNGO-SVM sticking warning model achieves an accuracy of 97.3333%， and is significantly higher in prediction accuracy and operating speed than WOA-SVM， NGO-SVM and SSA-SVM models. The SCNGO-SVM method provides a theoretical guidance for sticking prediction and its engineering applications.

sticking warning model;NGO;performance test;refracted opposition-based learning;sine cosine

基金项目：国家自然科学基金重大科研仪器项目“钻井复杂工况井下实时智能识别系统研制”（52227804）；国家自然科学基金面上项目“底部钻具高频扭转振动响应机理及识别方法研究”（52274003）；国家自然科学基金青年科学基金项目“干热岩储层双重介质射孔簇内复杂多裂缝起裂及扩展机理研究”（52104001）。

0" 引" 言

张涛，等：基于井下参数的SCNGO-SVM卡钻预警方法研究

卡钻是典型的井下复杂工况之一，卡钻事故可能会导致钻具损坏、井眼破坏，延长非必要作业时间，增加钻井成本。据统计，卡钻事故占整个钻井复杂情况的40%～50%，严重影响钻井作业的速度，导致一系列的安全和经济等方面的问题［1］。因此，为了预测井眼不清洁引起的卡钻事故，需要对井下参数进行机理分析，建立一种卡钻识别的预警模型。国内外学者对卡钻预测方法研究越来越多，这对智能钻井技术的发展具有重要的工程应用价值。

卡钻预测模型的构建是一个复杂的过程，受地质条件、钻具组合、测量设备等多种因素影响，建立卡钻预测模型大多需要大量的数据驱动。随着智能钻井技术的发展，通过对井下测量数据的分析，可以使用智能算法对井下复杂工况进行解释。富浩等［2-3］通过对井下测量数据的时域分析，建立了一种主成分分析-支持向量机的卡钻预测模型和K-means聚类的预测模型。刘景峰等［4］将摩阻扭矩分段计算模型与基于群体训练优化算法耦合，利用训练得到最优摩阻系数，开展模型计算预测值与现场监测数据的对比，并计算卡钻风险预测系数，实现钻进过程中卡钻风险的实时预测。WANG J.H.等［5］考虑钻井参数的时序特性，建立了基于长短时记忆网络的智能预测模型。I.AIBAIYAT等［6］使用人工神经网络和支持向量机预测卡钻。T.KANEKO等［7］建立现场井历史数据的数据驱动模型与物理模型，根据历史数据和当前实测数据以及经过训练的模型的估计，计算出卡钻发生的风险。结果表明，支持向量机比人工神经网络在卡钻事故预测中更准确。受限于高精尖的井下测量工具，目前卡钻风险的预测大多以地面数据［8-10］作为特征进行研究，而对于井下数据的研究比较少。尽管上述算法取得了比较好的预测效果，但大多数模型调用参数困难，需要一定的经验。

因此，研究基于井下数据和智能优化算法的卡钻模型，以提高模型的识别精度。针对卡钻风险预测的问题，提出了一种融合正余弦和折射反向学习的北方苍鹰优化算法（SCNGO）和支持向量机（SVM）的卡钻预警模型。

首先，针对北方苍鹰算法（NGO）容易陷入局部最优以及初始解分布具有的随机性和非均匀性的特性，引入折射反向学习策略初始化北方苍鹰算法个体、正余弦策略替换原始苍鹰算法的勘察阶段的位置更新公式和正余弦策略的步长搜索因子等进行改进；其次，将SCNGO算法用于SVM寻参；最后，将模型SCNGO-SVM应用于卡钻预警，提高模型的收敛速度和识别精度。所建立的卡钻预测模型能够有效地解决上述问题，可为钻井作业和卡钻的识别提供理论指导。

1" 算法原理及改进算法

1.1" 支持向量机

支持向量机是一种通过寻找一个最优超平面将样本分离开的算法类型。分离超平面可由法向量ω（决定了超平面的方向）和位移b（决定了超平面与原点间的距离）确定，则有：

ωx+b=0（1）

假设给定一个特征空间上的训练数据集T=x1，y1，x2，y2，…，xN，yN，其中x为特征向量，y为类标记。对于给定的数据集T和超平面ωx+b=0，通过引入松弛变量和惩罚因子对违反不等式约束的样本进行惩罚，若满足yωx+b=0≥1-ζi，其中i=1，2，…，N，可以得到极小化问题表达式为：

minω=12ω2+C∑Ni=1ζi（2）

式中：ζi为松弛变量，近似表示被误分类的样本数；C为惩罚因子，用来实现最大化分类间隔和最小化错分样本数之间的折中，是影响SVM分类性能的重要参数之一，称为超参数。

若满足∑Ni=1αiyi=0，其中0≤αi≤C，i=0，1，…，N，由式（2）得到对偶问题表达式为：

maxWα=∑Ni=1αi-12∑Ni，j=1yiyjαiαjKxi，xj（3）

式中：αi为拉格朗日乘子，Kxi，yj为核函数。

采用高斯径向基核函数，其表达式为：

Kxi，yj=e-g1xi-yj（4）

式中：g1为gama核参数函数，是影响SVM分类性能的另一个超参数。

引入核函数，从而得到分类的决策函数为：

fx=sgn∑Ni=1αiyiKxi，x+b（5）

由以上的理论分析可得，SVM模型的精度和优化主要取决于2个超参数C和g1，2个超参数的选择直接决定模型的精度和相关性能。

1.2" 北方苍鹰算法

北方苍鹰算法（Northern Goshawk Optimization，NGO）由M.DEHGHANI等［11］于2022年提出，该算法模拟了北方苍鹰捕猎过程中的行为，主要包括探索阶段（猎物识别和攻击）和开发阶段（追逐及逃生）。NGO算法中表示北方苍鹰的种群矩阵为：

X=X1XiXNN×m=x1，1" …" x1，j" …" x1，m

xi，1" …" xi，j" …" xi，m

xN，1" …" xN，j" …" xN，m

N×m

（6）

式中：X为北方苍鹰的种群矩阵，Xi为第i只北方苍鹰的位置，xi，j为第i只北方苍鹰的第j维的位置坐标，N为北方苍鹰种群成员的数量，m为问题变量的数量。

对于目标函数获得的式（6）中这些值可以表示为向量：

Fx=F1=FX1

Fi=FXi

FN=FXNN×1（7）

式中：Fx为北方苍鹰种群的目标函数向量；Fi为第

i只北方苍鹰的目标函数值，i=1，2，…，N。

探索阶段是北方苍鹰在狩猎的第1阶段。随机选择一个猎物，然后迅速攻击它。由于在搜索空间中随机选择猎物，这一阶段增加了NGO的探索能力。该阶段对搜索空间进行全局搜索，目的是识别最优区域。猎物选择和攻击的行为可以表示为：

Pi=Xk" i=1，2，…，N；k=1，2，…，

i-1，i，i+1，…，N（8）

xnew，p1i，j=xi，j+rpi，j-Ixi，j" Fpi＜Fi

xi，j+rpi，j-xi，j" Fpi≥Fi

（9）

Xi=Xnew，p1i" Fnew，p1i＜Fi

Xi" Fnew，p1i≥Fi

（10）

式中：Pi为第i只北方苍鹰的猎物的位置；k为区间1，N中的随机自然数；xnew，p1i，j为第i只北方苍鹰的第j维的新位置；xi，j为第i只北方苍鹰的第j维的位置；pi，j为第i只北方苍鹰的猎物的第j维的位置；Fpi为第i只北方苍鹰的猎物的位置的目标函数值；Fi 为Fpi对应的适应度；Xnew，p1i为第i只北方苍鹰的新位置；Fnew，p1i为其基于NGO第1阶段更新后第i只北方苍鹰的目标函数值；r为区间0，1中的随机数；I为一个特定随机数，取1或2；参数r和I为用于在搜索和更新中生成随机NGO行为的随机数。

北方苍鹰狩猎的第2阶段是开发阶段。在北方苍鹰攻击猎物后，猎物会试图逃跑。因此，在尾随和追赶的过程中，北方苍鹰继续追赶猎物。由于北方苍鹰的高速度，它们几乎可以在任何情况下追赶猎物，并最终猎获。对这种行为的模拟，提高了算法对搜索空间的局部搜索能力，该算法如式（11）～式（13）所示：

xnew，p2i，j=xi，j+R2r-1xi，j（11）

假定这种狩猎是封闭在以猎物出现位置为圆心、半径为R的攻击范围，则有：

R=0.021-tT（12）

式中：t为迭代计数器计数值，T为最大迭代次数。

Xi=Xnew，p2i" Fnew，p2i＜Fi

Xi" Fnew，p2i≥Fi

（13）

式中：Xnew，p2i为基于第2阶段更新后第i只北方苍鹰新位置，xnew，p2i，j为基于第2阶段更新后第i只北方苍鹰的第j维度的新位置，Fnew，p2i为基于第2阶段更新后第i只北方苍鹰的目标函数值。

NGO算法具有较好的收敛性和稳定性，但存在如下问题［12］：①初始解的分布具有随机性和非均匀性，群体中的个体素质参差不齐，极易造成群体多样性丧失，不能得到最优解；②NGO中的捕食者在第2阶段的捕食过程中，对其捕食过程进行了快速的跟踪，容易在后期开发过程中陷入局部极值。

1.3" 改进北方苍鹰算法

采用折射反向学习策略初始化北方苍鹰算法个体，其基本思想是通过计算当前解的反向解来扩大搜索范围，借此找出给定问题更好的备选解。折射反向学习原理如图1所示。

已知解在x轴上的搜索区间为a，b，原点O为a，b上的中点，法线为y轴，入射角和折射角分别为α和β，入射光线和折射光线的长度分别为l和l*。由此可得折射率n计算式：

n=sin αcos β=a+b2-xi，jx*i，j-a+b2·l*l（14）

令δ=ll*，代入式（14）并将其拓展到多维空间可得折射方向解：

x*i，j=ai+bj2+ai+bj2δ-xi，jδ（15）

式中：x*i，j为xi，j的折射反向解；ai和bj分别为搜索空间在j维度的下界和上界。

正余弦策略［13］是基于正弦余弦函数性质提出的一种元启发式算法，主要利用了正弦、余弦函数的震荡性，以不断逼近全局最优。采用正余弦策略替换原始苍鹰算法的勘察阶段的位置更新公式如下：

xi，jt+1=xi，jt+R1sinR2×

R3·bestxj-xi，jt" R4＜0.5

xi，jt+R1cosR2×

R3·bestxj-xi，jt" R4≥0.5

（16）

式中：xi，j t和xi，jt+1分别为第i只北方苍鹰在t和t+1次迭代时的位置在第j维的分量；R1、R2、R3及R4为随机参数，其中R1=21-tT，R2∈U0，2π，R3∈U0，2，R4∈U0，4，U表示均匀分布。

在算法局部开发阶段引入改进后的正余弦算法，利用正余弦函数的震荡性来维持算法迭代后期种群多样性，以加强算法的局部寻优能力。

对正余弦策略的步长搜索因子进行改进。原始步长搜索因子呈线性递减趋势，不利于进一步平衡北方苍鹰算法的全局搜索和局部开发能力。因子调整公式为：

r′1=1-1-tTλ1λ（17）

ω1=etT-1e-1（18）

xnew，p1i，j=xi，j+r′pi，j-Ixi，j" Fpi＜Fi

xi，j+r′pi，j-xi，j" Fpi≥Fi

（19）

式中：ω1为非线性权重因子；r′1为步长搜素因子；λ为调节参数，λ≥1，取值为1.2。

1.4" SCNGO-SVM模型

为了使卡钻识别效果达到最好，通过SCNGO算法对SVM的惩罚因子C和核参数g1进行寻优，构建了SCNGO-SVM的卡钻预测模型，其具体算法寻优流程如图2所示，具体步骤如下。

（1） 初始化参数，包括鹰个体数量、迭代次数、适应度函数等，以及SVM的惩罚因子C和核参数g1。

（2） 随机生成初始鹰群种群，采用折射反向学习策略初始化北方苍鹰算法个体，计算每个鹰个体的适应度，保存目前最优解与适应度值，根据式（8）随机选择猎物。

（3） 引进正余弦策略的步长搜索因子，根据式（9）更新第i只北方苍鹰在第j维新位置的最优解。

（4） 根据式（19）更新第i只北方苍鹰的位置向量。

（5） 根据式（11）、式（17）计算第2阶段的第i只北方苍鹰在第j维的位置。

（6） 根据式（13）更新第2阶段第i只北方苍鹰的位置向量。

（7） 若达到最大迭代次数，则将北方苍鹰最优解对应参数惩罚因子C和核参数g1赋予SVM，结束算法。否则，返回执行步骤（3）。

2" SCNGO算法性能测试

2.1" 基准测试函数

为了验证算法的寻优能力，分别选择2个典型的单峰测试函数、2个典型的多峰测试函数和2个典型的固定维多峰测试函数，对算法的寻优能力进行测试。选取的基准测试函数相关参数如表1所示。

2.2" 算法性能比较

为了验证SCNGO算法的优越性，选取6个基本测试函数，通过与北方苍鹰优化算法（NGO）、鲸鱼优化算法（Whale optimization algorithm，WOA）、麻雀优化算法（Sparrow Search Algorithm，SSA）寻优比对来验证SCNGO的优越性，种群规模设置为30，最大迭代次数为500。为了降低随机误差对结果的影响，对6个测试函数分别进行了30次独立试验。求最差值、最优值、平均值及标准差，计算结果如表2所示。SCNGO算法在单峰、多峰函数中均能达到理论最优值，表明SCNGO具有更强的全局寻优和局部搜寻的能力，且在最差值、最优值、平均值和标准差的计算上同样优于其他算法。

为了验证算法的收敛速度、寻优精度，分别用4种智能算法对6个基准测试函数进行迭代寻优，各函数的迭代曲线如图3所示。NGO算法、WOA算法和SSA算法收敛曲线变化相对平稳，而SCNGO算法收敛曲线为先大幅度下降后趋于稳定，收敛精度和速度明显优于其他算法。这是由于对正余弦策略的步长搜索因子进行改进，对其最优位置不断进行调整，增强了其全局寻优和局部搜寻的能力，且用正余弦策略替换原始苍鹰算法的勘察阶段的位置，可加强北方苍鹰位置的灵动性，进一步提升算法后期的局部优化能力，提高了收敛精度。

由上述分析可知，SCNGO算法的寻优能力、收敛速度及寻优精度等优于NGO、SSA、WOA算法。

3" SCNGO-SVM卡钻预警试验

3.1" 数据来源

以四川某井现场试验所获得的数据为例，测量工具为北京信息科技大学研制的近钻头多参数测量短节。测量参数包括钻压（±300 kN）、扭矩（±30 kN·m）、温度（150 ℃）、内外压（100 MPa）、三轴振动加速度（±40g）、转速（±333 r/min）等9个参数（g为重力加速度）。由于测量工具距离钻头近，所测数据能够有效地反映井下钻具的工作状态。

3.2" 试验钻具组合

试验时钻具组合为：215.9 mm PDC钻头+测量短节+172.0 mm 1.5°弯螺杆+止回阀 +定向接头+127.0 mm无磁承压钻杆 +127.0 mm加重钻杆2根+165.1 mm震击器 +127.0 mm加重钻杆6根 +127.0 mm钻杆6根+172.0 mm水力推进器+127.0 mm钻杆5根 +旋流清砂器+127.0 mm钻杆+DS411×DS520转换接头×0.73 m+139.7 mm钻杆至井口。

3.3" 井下测量数据的卡钻工况分析

这次试验累计工作61 h，实测数据特征如图4所示。

drilling and before and after sticking

当钻井作业钻至卡钻发生前时，司钻发现随着地面施加的钻压增大，扭矩迅速增大并伴随着剧烈的振动，此时钻具在井筒内不能自由活动，从而判断井底发生了卡钻。井下数据显示，卡钻发生前，三轴振动相较于正常钻井时变得剧烈，主要发生在横截面上，轴向振动无明显变化，而且扭矩迅速变大，此为卡钻前的预兆。卡钻前的征兆数据来自图4区间Ⅱ，正常钻进的数据来源于图4区间Ⅰ，区间Ⅲ表示卡钻发生后的数据变化特征。结合数据分析可知，卡钻在振动上的表现主要在横向振动，轴向振动基本无明显变化，同时伴随着扭矩的迅速增大。

3.4" 对比分析

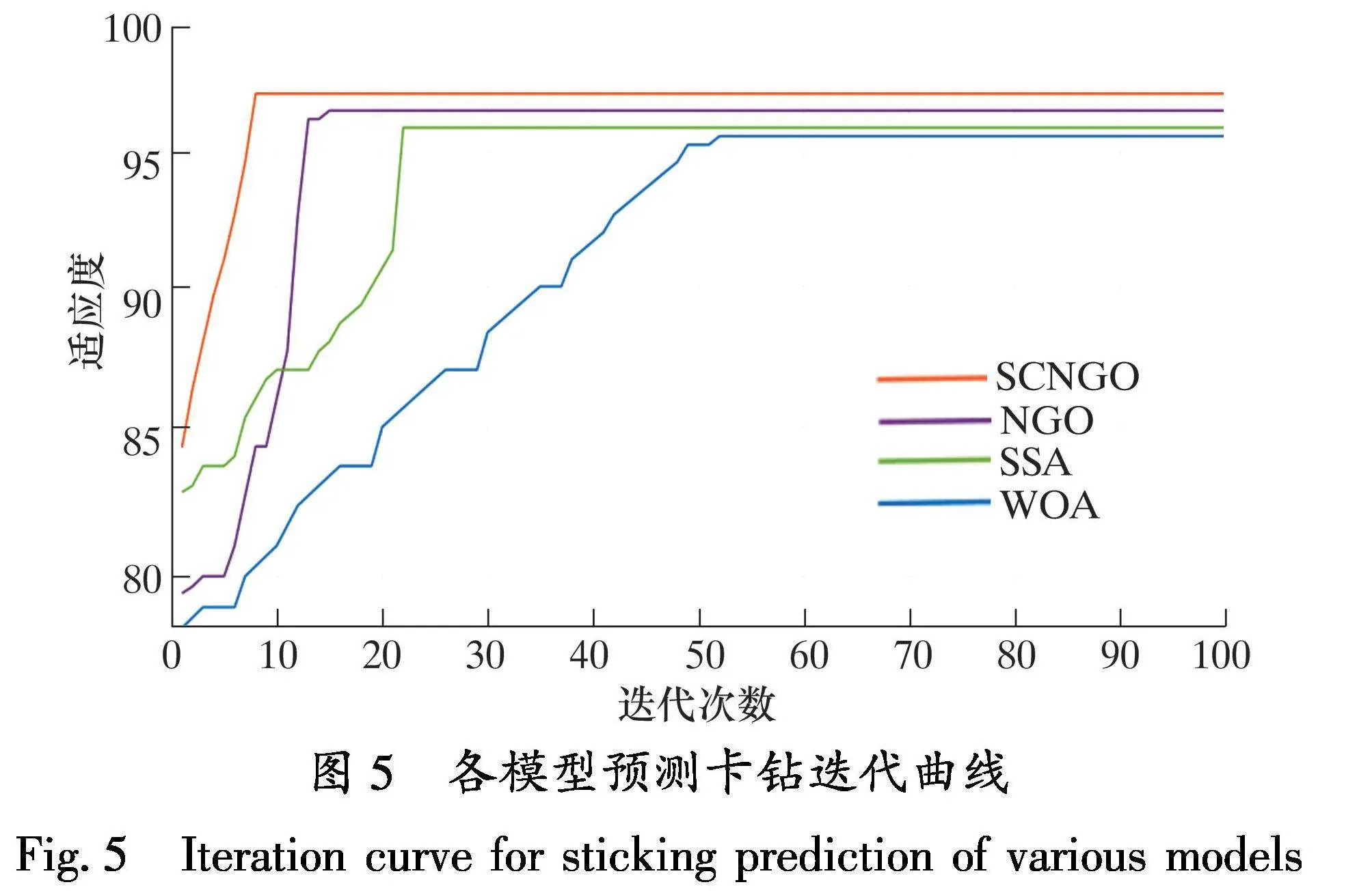
在相同的训练集和测试集情况下，按照图4所示的区域分别提取卡钻前的特征数据和正常钻进状态下对应的特征数据，总共1 000组数据，正常钻进数据和卡钻前的特征数据各500组。数据特征包括钻压、扭矩、x轴振动加速度、y轴振动加速度、z轴振动加速度，共5类特征。按照7∶3的比例划分训练集与测试集，进行卡钻事故的预测。分别建立SCNGO、NGO、SSA和WOA算法优化SVM的卡钻预警模型。统一设置最大迭代次数为100，种群数量为30。4种算法优化SVM的卡钻预警模型的适应度曲线以及分类准确率如图5和图6所示。

由图5可知，使用SCNGO算法仅需要迭代8次，就可以找到最佳的SVM的超参数。而NGO、SSA、WOA分别需要迭代15次、22次和52次才可以找到各自最佳适应度，并且适应度均没有SCNGO算法的最佳适应度数值大。这说明SCNGO优化算法相较与其他优化算法能够快速、准确地找到SVM的超参数。

将4种算法分别用于优化SVM模型的超参数，构建卡钻预警模型，结果如表3所示。

通过4种算法的对比分析可知，SCNGO-SVM模型优于其他模型。图6中，标签1代表卡钻类型，标签0代表正常钻进。SCNGO-SVM模型的分类准确率可达97.33%，比NGO-SVM、SSA-SVM、WOA-SVM模型的分类准确率分别提高0.68%，1.38%，1.73%。结果表明，SCNGO算法不仅在寻找最优参数方面速度快，结合SVM之后，它的分类预测准确率也比其他智能优化算法更高，效果显著。

在相同测试集和训练集的情况下，4种模型的性能参数如表3所示。SCNGO-SVM准确率优于NGO-SVM、WOA-SVM及SSA-SVM。分析结果说明，SVM模型的精度和优化主要取决于2个超参数C和g1，2个超参数的选择直接决定模型的精度和相关性能。SCNGO能够根据数据的特点选择合适的超参数，以提高卡钻预测的精度。

4" 结论及建议

提出了一种融合正余弦和折射反向学习的北方苍鹰优化算法（SCNGO算法），并用于SVM超参数寻优，建立了卡钻预警模型，得到以下结论。

（1）使用基准测试函数对智能优化算法进行寻优性能分析，结果表明，SCNGO算法在收敛速度、寻优精度等方面明显优于NGO算法、WOA算法及SSA算法。

（2）提出的SCNGO-SVM卡钻预警模型，对于卡钻的预测准确率高达97.33%，相较于WOA-SVM、NGO-SVM、SSA-SVM卡钻预警模型，在预测准确率和运算速度上均有显著提升。

（3）本文只针对井眼不清洁造成的卡钻进行了试验分析，其他因素造成的卡钻情况还有待试验验证。建议后续（用此该模型）开展相应的卡钻风险预测，对模型的准确性及性能进一步验证。

［1］" "朱硕．基于机理模型与数据模型的卡钻智能预测方法［D］．北京：中国石油大学（北京），2022．

ZHU S. Intelligent prediction method of sticking based on coupling mechanism and data model［D］. Beijing： China University of Petroleum（Beijing）， 2022.

［2］" 富浩，张涛，李玉梅，等．基于井下参数的PCA-SVM卡钻预测研究［J］．计算机仿真，2021，38（12）：386-390．

FU H， ZHANG T， LI Y M， et al. Research on PCA-SVM stuck prediction based on downhole parameters［J］. Computer Simulation， 2021， 38（12）： 386-390.

［3］" 苏晓眉，张涛，李玉飞，等．基于K-Means聚类算法的沉砂卡钻预测方法研究［J］．钻采工艺，2021，44（3）：5-9．

SU X M， ZHANG T， LI Y F， et al. Research on the sticking prediction method based on K-Means clustering algorithm［J］. Drilling amp; Production Technology， 2021， 44（3）： 5-9.

［4］" 刘景峰，袁旭，龙远，等．考虑岩屑影响的智能实时卡钻风险预测［J］．中国科技论文，2023，18（9）：1007-1014．

LIU J F， YUAN X， LONG Y， et al. Intelligent real time stuck pipe risk prediction considering the effect of cuttings［J］. China Sciencepaper， 2023， 18（9）： 1007-1014.

［5］" WANG J H， GUAN Z， LIU M C， et al. Drilling stuck probability intelligent prediction based on LSTM considering local interpretability［C］∥the 57th U.S. Rock Mechanics/Geomechanics Symposium. Atlanta， Georgia： ARMA， 2023： ARMA 2023-0326.

［6］

AI-BAIYAT I， HEINZE L. Implementing artificial neural networks and support vector machines in stuck pipe prediction［C］∥SPE Kuwait International Petroleum Conference and Exhibition. Kuwait City， Kuwait： SPE， 2012： SPE 163370-MS.

［7］" KANEKO T， INOUE T， NAKAGAWA Y， et al. Hybrid approach using physical insights and data science for Stuck-Pipe prediction［J］. SPE Journal， 2024， 29（2）： 641-650.

［8］" 李紫璇，张菲菲，祝钰明，等．钻井模型与机器学习耦合的实时卡钻预警技术［J］．石油机械，2022，50（4）：15-21，93．

LI Z X， ZHANG F F， ZHU Y M， et al. Real-time pipe sticking early warning technology based on coupling of drilling model and machine learning［J］. China Petroleum Machinery， 2022， 50（4）： 15-21， 93.

［9］" SABAH M， MEHRAD M， ASHRAFI S B， et al. Hybrid machine learning algorithms to enhance lost-circulation prediction and management in the Marun oil field［J］. Journal of Petroleum Science and Engineering， 2021， 198： 108125.

［10］" MALKI M A， ABUGHABAN M F， GUIMARAES T T， et al. Stuck pipe prediction model to detect and notify rig crew based on drilling parameters and physical models outputs［C］∥SPE/IADC Middle East Drilling Technology Conference and Exhibition. Abu Dhabi， UAE： SPE， 2023： SPE 214604-MS.

［11］" DEHGHANI M， HUBLOVSK， TROJOVSKP. Northern goshawk optimization： a new swarm-based algorithm for solving optimization problems［J］. IEEE Access， 2021， 9： 162059-162080.

［12］" 任志玲，张景智．多策略融合LSSVM-NGO的滑动电接触失效诊断［J］．电子测量与仪器学报，2023，37（12）：37-47．

REN Z L， ZHANG J Z. Multi-strategy fusion of LSSVM-NGO for sliding electrical contact failure diagnosis［J］. Journal of Electronic Measurement and Instrumentation， 2023， 37（12）： 37-47.

［13］" MIRJALILI S. SCA： A sine cosine algorithm for solving optimization problems［J］. Knowledge-based Systems， 2016， 96： 120-133.