基于Hermite公式和扩展三次B-样条的Burgers方程数值解法

摘要：将Hermite公式与扩展三次B-样条相结合，给出了一种求解 Burgers方程的混合格式计算方法.对Burgers方程空间离散采用Hermite公式结合扩展三次B-样条配点法，时间离散采用有限差分法，利用Von Neumann（Fourier）分析法证明了混合格式的稳定性，数值实验验证了方法的准确性和有效性.适当调整基函数中的参数可以提高计算精度.

关键词：Hermite公式；Burgers方程；扩展三次B-样条；有限差分

中图分类号：O 241.8""" 文献标志码：A""" 文章编号：1001-988Ⅹ（2025）01-0111-06

DOI：10.16783/j.cnki.nwnuz.2025.01.016

收稿日期：20230929;修改稿收到日期：20240401

基金项目：国家自然科学基金资助项目（11502141）

作者简介：周书伊（1997—），女，安徽宿州人，硕士.主要研究方向为微分方程数值解.

Email：soyicheer@163.com

*通信联系人，女，副教授，博士，硕士研究生导师.主要研究方向为数值计算.

Email：wu@sheip.edu.cn

Numerical solution of Burgers equation based on Hermite formula

and extended cubic B-spline

ZHOU Shu-yi，WU Bei-bei，XU Li

（School of Mathematics and Physics，Shanghai University of Electric Power，Shanghai 200090，China）

Abstract：By combining Hermite formula with the extended cubic B-spline，an efficient computational method is presented for solving the Burgers equation in a mixed format.The spatial discretization for the Burgers equation is achieved by employing Hermite formula in conjunction with the extended cubic B-spline collocation method，while the temporal discretization is implemented using finite difference.The stability of this format is proved using the Von Neumann（Fourier） analysis method.A numerical experiment is performed to illustrate the accuracy and effectiveness of the proposed algorithm.The calculation accuracy can be improved by appropriately adjusting the parameter" within the basis functions.

Key words：Hermite formula;Burgers equation;extended cubic B-spline;finite difference

Burgers方程是一种模拟激波传播和反射的非线性偏微分方程，它可应用于诸多领域，如流体力学、非线性声学和气体动力学等.Burgers方程描述了流体中湍流的变化情况，是理解湍流的重要工具［1］.因此，Burgers方程数值解的研究具有十分重要的理论和实际意义.

目前求解Burgers方程的数值方法有很多种，主要包括对角Padé逼近法［2］、有限元法［3-7］、变分迭代法［8］等.除此之外，B-样条也被许多学者用来处理Burgers方程，如用三次样条来处理Burgers方程［9，10］，用B-样条的配置法进行Burgers方程的数值处理［11，12］；用样条函数和准线性化来求Burgers方程的数值解［13］；用B-样条［14］和三次B-样条插值［15-17］对Burgers方程进行空间离散；用Hermite公式给二阶导数一个新的近似值，将Hermite方程与三次B-样条函数结合计算Burgers方程的数值解［18，19］等.

本文结合Hermite公式及扩展三次B-样条配点法计算Burgers方程数值解，时间离散采用有限差分法，空间离散采用Hermite公式和扩展三次B-样条配点法.用标准Von Neumann方法进行稳定性分析，数值实验表明，Hermite公式结合扩展三次B-样条配点法求解Burgers方程是有效的，适当调整扩展三次B-样条基函数中自由参数的值，可以提高逼近程度，数值结果好于文献［11，19-21］.

1" Burgers方程

考虑Burgers方程

U（x，t）t+UU（x，t）x-ρ2Ux2=0，

a≤x≤b，0≤t≤T，

初始条件为

U（x，0）=f（x），（2）

边界条件为

U（a，t）=g1（t）， U（b，t）=g2（t）.（3）

其中，U为关于x，t的二元函数，ρ（ρgt;0）为粘性系数，t和x分别为时间和位置.

2" 扩展三次B-样条配点法

以空间步长h和时间步长τ将求解区域［a，b］×［0，T］划分为均匀网格，其中τ=T/M，h=（b-a）/N，将tk=kτ（k=0，1，2，…，M），xj=jh（j=0，1，2，…，N）作为时间和空间域的划分，其网格点记为（xj，tk）.

为了得到方程（1）精确解U（x，t）的近似解u（x，t），可以利用扩展三次B-样条基函数配点法将近似解表示为

u（x，t）=∑N-1j=-1cj（t）Ej（x），（4）

其中cj（t）是与时间t相关的未知量，Ej（x）是扩展三次B-样条基函数，定义为［22］

Ej（x）=

1h3

4h（1-λ）（x-xj）3+

3λ（x-xj）4， x∈［xj，xj+1］，

（4-λ）h4+12h3（x-xj+1）+

6h2（2+λ）（x-xj+1）2-

12h（x-xj+1）3-

3λ（x-xj+1）4，

x∈［xj+1，xj+2］，

（4-λ）h4+12h3（xj+3-x）+

6h2（2+λ）（xj+3-x）2-

12h（xj+3-x）3-

3λ（xj+3-x）4，

x∈［xj+2，xj+3］，

4h（1-λ）（xj+4-x）3+

3λ（xj+4-x）4，

x∈［xj+3，xj+4］，

0， 其他，（5）

其中λ为自由参数.

表1给出了函数Ej（x）及其一阶、二阶导数在节点处的值，其中

φ1=4-λ24， φ2=8+λ12， φ3=-12h，

φ4=2+λ2h2， φ5=-2-λh2.

根据表1，近似解ukj及其关于x的一阶和二阶导数分别为

ukj=φ1ckj-1+φ2ckj+φ1ckj+1，

（ux）kj=-φ3ckj-1+φ3ckj+1，

（uxx）kj=φ4ckj-1+φ5ckj+φ4ckj+1.（6）

记点（xj，tk）处的近似解为ukj=u（xj，tk），在区间［xj，xj+1］上的定义为

u（xj，tk）=ukj=∑j+1l=j-1ckl（t）El（x）.（7）

将方程（1）的时间和空间导数进行离散得到

uk+1j-ukjτ+（uux）k+1j-（uux）kj2=

ρ（uxx）k+1j+（uxx）kj2.（8）

利用文献［19］的方法对（8）式中的uux进行拟线性化处理，得到

（uux）k+1j=ukj（ux）k+1j+uk+1j（ux）kj-

（uux）kj，（9）

结合（8）式可得

uk+1j+τ2（ukj（ux）k+1j+uk+1j（ux）kj）-τρ2（uxx）k+1j=

ukj+τρ2（uxx）kj.（10）

利用文献［1，18，23，24］中的Hermite公式

（uxx）kj-1+10（uxx）kj+（uxx）kj+1-

12h（ukj-1-2ukj+ukj+1）=O（h4），（11）

将（11）式代入（10）式可得

uk+1j+τ2（ukj（ux）k+1j+uk+1j（ux）kj）+

τρ20（（uxx）k+1j-1+（uxx）k+1j+1-

12h2（uk+1j-1-2uk+1j+uk+1j+1））=

unj-

τρ20（（uxx）kj-1+（uxx）kj+1-

12h2（ukj-1-2ukj+ukj+1））.（12）

将（7）式代入（12）式可得

m00ck+1j-2+m1jck+1j-1+m2jck+1j+

m3jck+1j+1+m00ck+1j+2=

-m00ckj-2+n11ckj-1+n22ckj+

n11ckj+1-m00ckj+2，

j=1，2，3，…，N-1，（13）

其中

m00=ρτφ420-2ρτφ15h2，

m1j=1+6ρτ5h2φ1+ρτφ520-3ρτφ25h2+

τ2（ux）kjφ1-τ2ukjφ3，

m2j=1+6ρτ5h2φ2+ρτφ410-6ρτφ15h2+

τ2（ux）kjφ2+τ2ukjφ3，

m3j=1+6ρτ5h2φ1+ρτφ520-3ρτφ25h2+

τ2（ux）kjφ1+τ2ukjφ3，

n11=1-6ρτ5h2φ1-ρτφ520+3ρτφ25h2，

n22=1-6ρτ5h2φ2-ρτφ420+6ρτφ15h2.

将（7）式代入（10）式得到j=0，N时的方程

φ1-ρτ2φ4+τ2φ1（ux）kj-τ2φ3ukjck+1j-1+

φ2-ρτ2φ5+τ2φ2（ux）kjck+1j+

φ1-ρτ2φ4+τ2φ1（ux）kj+τ2φ3ukjck+1j+1=

φ1+ρτ2φ4ckj-1+φ2+ρτ2φ5ckj+

φ1+ρτ2φ4ckj+1， j=0，N.

（13）和（14）式中包含了N+3个未知量Cn+1=（cn+1-1，cn+10，cn+11，…，cn+1N+1）的N+1个线性方程组.为了使方程组有唯一解，需要利用给定的边界条件得到另外两个附加方程，其解可以使用任何基于高斯消去的算法获得.

初始向量C0=［c0-1，c00，c01，…，c0N+1］T可以根据下列条件给出：

ux（x0，0）=f′（x0），

u（xj，0）=f（xj）， j=0，1，2，…，N，

ux（xN，0）=f′（xN）.

对应的矩阵形式为

AC0=B，（15）

其中

A=

-φ30φ30…0000

φ1φ2φ10…0000

0φ1φ2φ1…0000

0000…φ1φ2φ10

0000…0φ1φ2φ1

0000…0φ30-φ3

B=［f′（x0），f（x0），…，f（xN），f′（xN）］T.

当初始向量已知，便可以根据递推关系（13）和（14）得出向量Ck的时间演化形式，进而计算第（k+1）时间层的近似解uk+1j.

3" 稳定性分析

现采用Von Neumann方法研究计算格式的稳定性，利用文献［19］的方法，用常数d代替ux将uux线性化，再根据（10）式可得

uk+1j+τ2duk+1j-τρ2（uxx）k+1j=

ukj-τ2dukj+τρ2（uxx）kj.（16）

利用Hermite公式（11）得到

uk+1j+τ2duk+1j+τρ20（uxx）k+1j-1+（uxx）k+1j+1-

12h2（uk+1j-1-2uk+1j+uk+1j+1）=

ukj-τ2dukj-τρ20（uxx）kj-1+（uxx）kj+1-

12h2（ukj-1-2ukj+ukj+1），（17）

将（7）式代入（17）式，有

z0ck+1j-2+z1ck+1j-1+z2ck+1j+z1ck+1j+1+z0ck+1j+2=

w0ckj-2+w1ckj-1+w2ckj+

w1ckj+1-w0ckj+2，（18）

z0=ρτφ420-3ρτφ15h2，

z1=1+6ρτ5h2φ1+ρτφ520-3ρτφ25h2+τ2dφ1，

z2=1+6ρτ5h2φ2+ρτφ410-6ρτφ15h2+τ2dφ2，

w0=-ρτφ420+3ρτφ15h2，

w1=1-6ρτ5h2φ1-ρτφ520+3ρτφ25h2-τ2dφ1，

w2=1-6ρτ5h2φ2-ρτφ410+6ρτφ15h2-τ2dφ2.

将傅里叶格式ckj=ξkexp（ijηh）代入（18）式，其中η是波速，i=-1是虚数单位，可得

z0ξk+1ei（j-2）ηh+z1ξk+1ei（j-1）ηh+z2ξk+1eijηh+

z1ξk+1ei（j+1）ηh+z0ξk+1ei（j+2）ηh=

w0ξkei（j-2）ηh+w1ξkei（j-1）ηh+w2ξkeijηh+

w1ξkei（j+1）ηh+w0ξkei（j+2）ηh，

化简得

ξ=2w0cosηh+2w1cosηh+w22z0cos2ηh+2z1cosηh+z2.

要保证（18）式稳定，需要满足｜ξ｜lt;1.在η∈［-π，π］时，不失一般性，可以假设η=0，因此上述方程简化为

ξ=2w0+2w1+w22z0+2z1+z2lt;1，

这证明该格式是无条件稳定的.

4" 数值实验

下面通过数值实验对数值格式的精度进行检验，误差使用欧几里得范数L2和绝对范数L∞，即

L2=U-Uk22=h∑Nj=0（U（xj，tk）-Ukj）2，

L∞=U-Uk∞=maxjU（xj，tk）-Ukj.

考虑Burgers方程

Ut+UUx-ρ2Ux2=0，

0lt;xlt;1，tgt;0，

U（0，t）=U（1，t）=0，

其精确解为

U（x，t）=xt1+tt0expx24ρt，

t0=exp18ρ.

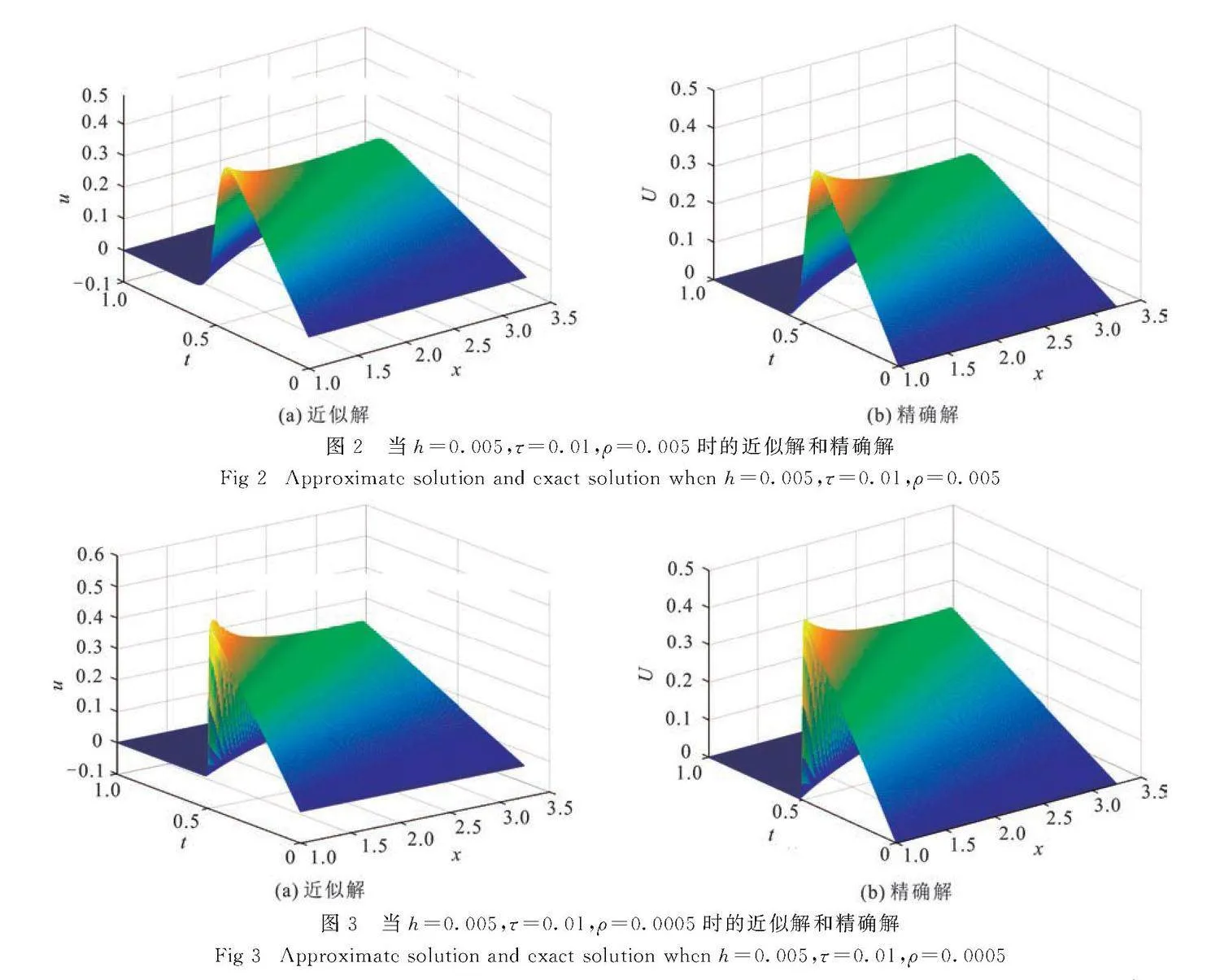
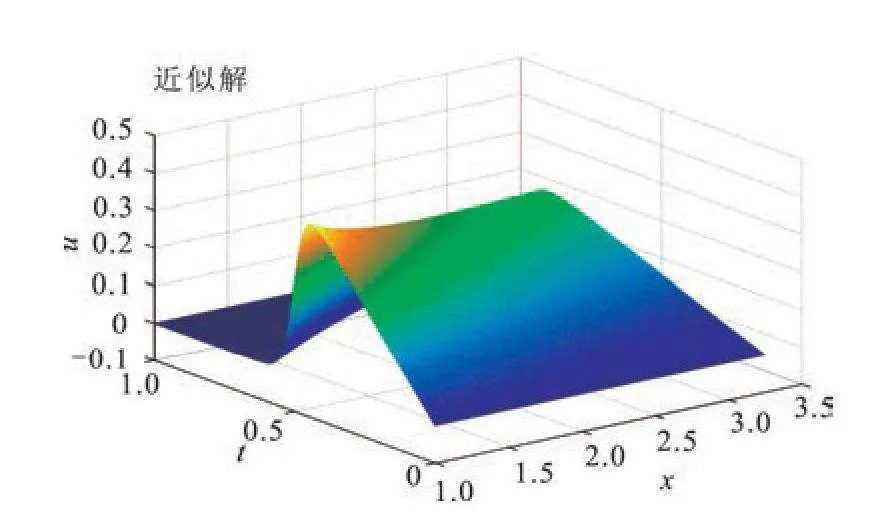
图1（a），（b）分别给出了不同时间段的近似解与精确解.图2和图3是选择不同粘性系数ρ值时近似解和精确解.

将本文方法与三次B-样条［11］、Hermite结合三次B-样条［19］、Galerkin方法［20］及基于三次样条［21］求解的误差范数L2和L∞进行对比，结果见表2和表3.

Fig 1Approximate solutions（circle，star，square，diamond） and exact solution（solid line） at different time stages

Fig 2Approximate solution and exact solution when h=0.005，τ=0.01，ρ=0.005

Fig 3Approximate solution and exact solution when h=0.005，τ=0.01，ρ=0.0005

5" 结论

本文结合Hermite公式和扩展三次B-样条基函数，提出了一种新的求解Burgers方程的方法.数值实验表明：该方法求解Burgers方程是有效的，通过选取适当的参数值ρ和λ，可以提高逼近效果；对于相同的离散方式和网格剖分，利用Hermite公式和扩展三次B-样条基函数结合的方法计算的相对误差小于文献［11，19-21］的方法，具有较高的数值精度.

参考文献：

［1］" BATEMAN H.Some recent researches on the motion of fluids［J］.Month Weather Rev，1915，43：163.

［2］" ALTIPARMAK K，ZI

瘙 塁" T.Numerical solution of Burgers equation with factorized diagonal Padé approximation［J］.Inter J Num Meth Heat Fluid Flow，2011，21（3）：310.

［3］" ARMINJON P，BEAUCHAMP C A.A finite element method for Burgers equation in hydrodynamics［J］.Inter J Numer Meth Eng，1978，12（3）：415.

［4］" CALDWELL J，WANLESS P，COOK A E.A finite element approach to Burgers equation［J］.Appl Math Model，1981，5（3）：189.

［5］" VAROGLU E，LIAMFINN W D.Space-time finite elements incorporating characteristics for the Burgers equation［J］.Inter J Num Meth Eng，1980，16（1）：171.

［6］" 许超，周家全，唐启立.Burgers方程特征混合有限元方法分析［J］.西北师范大学学报（自然科学版），2017，53（6）：6.

［7］" 刘万海，孙建安，豆福全，等.用五次B样条Galerkin有限元方法求Burgers方程的数值解［J］.西北师范大学学报（自然科学版），2009，45（2）：35.

［8］" SAUNDERS R，CALDWELL J，WANLESS P.A variational-iterative applied to Burgers equation［J］.IMA J Num Anal，2008，36（3）：349.

［9］" CALDWELL J.Application of cubic splines to the nonlinear Burgers equation［J］.Num Meth Nonl Probl，1987，3：253.

［10］" RUBIN S G，KHOSLA P K.Higher-order numerical solutions using cubic splines［J］.American Insti Aeronaut Astronaut，1976，14（7）：851.

［11］" DAGˇ，IRK D，SAHIN A.B-spline collocation methods for numerical solutions of the Burgers equation［J］.Math Probl Eng，2004，5：521.

［12］" DAGˇ，IRK D，SAKA B.A numerical solution of the Burgers equation using cubic B-splines［J］.Appl Math Comput，2005，163：199.

［13］" RUBIN S G，GRAVES R A.A Cubic Spline Approximation for Problems in Fluid Mechanics［R］.Nasa Technical Reports Server R-436，Washington，DC，1975，L-9929.

［14］" YOUSEFI M，RASHIDINIA J.YOUSEFI M，et al.Numerical solution of Burgers equation by B-spline collocation［J］.Afrika Mate，2016，27：1287.

［15］" JAIN P C，LOHAR B L.Cubic spline technique for coupled non-linear parabolic equations［J］.Comp Math Appl，1979，5（3）：179.

［16］" LOHAR B L，JAIN P C.Variable mesh cubic spline technique for N-wave solution of Burgers equation［J］.J Compu Phy，1981，39（2）：433.

［17］" NGUYEN H，REYNEN J.A space-time finite element approach to Burgers equation［C］//Numerical Methods for Nonlinear Problems，Lexington，US：Pineridge Press，1982，3：718.

［18］" YOUSAF A，YASEEN M.A cubic trigonometric B-spline collocation method based on Hermite formula for the numerical solution of the heat equation with classical and non-classical boundary conditions［J］.J Prime Res Math，2021，17（1）：95.

［19］" ABDULLAHA M，YASEENA M，SENBAN M D L.Efficient collocation method based on Hermite formula and cubic B-splines for numerical solution of the Burgers equation［J］.Math Comput Simul，2002，197：166.

［20］" ALI A H A，GARDNER L R T，GARDNER G A.A Galerkin approach to the solution of Burgers equation［J］.Appl Math Comput，1990，157（2）：331.

［21］" ALI A H A，GARDNER L R T，GARDNER G A.A collocation solution for Burgers equation using cubic splines［J］.Comput Method Appl Mechan Eng，1992，100（3）：325.

［22］" IRK D，DAG I，TOMBUL M.Extended cubic B-spline solution of the advection-diffusion equation［J］.KSCE J Civil Eng，2014，19（4）：929.

［23］" KHADER M M，ADEL M M.Numerical solution of fractional wave equation using an efficient class of FDM based on Hermite formula［J］.Adv Cont Differen Equat，2016，2016（34）：1.

［24］" YOUSAF A，ABDELJAWAD T，YASEEN M，et al.Novel cubic trigonometric B-spline approach based on Hermite formula for solving convection-diffusion equation［J］.Mathe Probl Eng，2020，2020（38）：1.

（责任编辑 "马宇鸿）