基于自掘性多尺度识别的隧道洞口老滑坡复活变形预测

摘要：为实现滑坡变形的高精度预测，以隧道洞口段复活滑坡为背景，利用变分模式分解开展滑坡变形数据的模态识别，并结合移动平均法进行趋势位移分析，将滑坡变形数据分解为趋势位移和随机位移；在滑坡变形数据分解基础上，利用猎食者算法和双向长短期记忆构建趋势位移预测模型，再在数据自掘性、多尺度分析基础上，通过BP神经网络或支持向量机实现随机位移预测．结果发现，受隧道洞口段施工影响，洞口滑坡变形特征显著，并由3个监测点的预测结果统计，得到预测结果的EMAP值介于2.01%～2.05%，Tt值介于162.45 ms～185.45 ms，预测模型不仅具有较优的预测精度，还具较强的稳定性，能有效掌握滑坡变形规律，为滑坡后续防治奠定了一定的理论基础．

关键词：滑坡；数据分解；变分模式分解；变形预测

中图分类号：P 642""" 文献标志码：A""" 文章编号：1001-988Ⅹ（2025）01-0093-09

DOI：10.16783/j.cnki.nwnuz.2025.01.014

收稿日期：20230906;修改稿收到日期：20241201

基金项目：国家自然科学基金资助项目（52278365）

作者简介：翟会君（1984—），女，河南济源人，高级工程师.主要研究方向为地质灾害危险性评估.

Email：zhj1231101@163.com

Prediction of resurrection deformation of old landslides

at tunnel entrances based on self excavation multi-scale recognition

ZHAI Hui-jun，ZHU Tao，ZHAI Ya-feng

（The Fourth Geological Exploration Institute of Henan Geology and Mineral Bureau，Zhengzhou 450000，Henan，China）

Abstract：In order to achieve high-precision prediction of landslide deformation，taking the revival of landslides in the tunnel entrance section as the background，the modal identification of landslide deformation data is carried out using variational mode decomposition，and the trend displacement is proposed by combining the moving average method.The landslide deformation data is decomposed into trend displacement and random displacement.Based on the decomposition of landslide deformation data，a trend displacement prediction model was constructed using the predator algorithm and bidirectional long short-term memory.Then，on the basis of data self excavation and multi-scale analysis，random displacement prediction was achieved through BP neural network or

support vector machine.The results showed that the deformation characteristics of the landslide at

the tunnel entrance was significant due to the construction of the tunnel entrance section，and the prediction results from three monitoring points were statistically analyzed.The EMAP value of the prediction results ranged from 2.01% to 2.05%，and the Tt value ranged from 162.45 ms to 185.45 ms，which not only had excellent prediction accuracy，but also had strong stability，and could effectively grasp the deformation law of the landslide，laying a certain theoretical foundation for subsequent landslide prevention and control.

Key words：landslide;data decomposition;decomposition of variational patterns;deformation prediction

在隧道建设过程中，受地质环境条件限制，隧道洞口段滑坡时有发生，严重威胁洞口安全，且鉴于滑坡变形是其各类稳定影响因素综合作用的体现，因此，开展隧道洞口段滑坡变形预测研究是必要的［1-2］．目前，刘传利等［3］开展了隧道斜交滑坡条件下的稳定性分析；李洋溢等［4］研究了隧道洞口滑坡的成因机制；刘传利等［5］探讨了隧道在滑坡段的进洞方案；李广利等［6］对隧道洞口滑坡成因及其防治进行了综合分析．上述研究成果多偏向于洞口滑坡成因、稳定性分析及防治研究等，均较少涉及此类滑坡的变形预测研究.为考虑到变形是各类稳定性影响因素的综合体现，以变形预测成果评价老滑坡复活稳定性具有可行性，因此，如何构建一个合理且高精度的老滑坡复活变形预测模型已发展成为一个热点研究问题．

根据Wang等［7］、Li等［8］研究表明，滑坡变形预测能为其稳定性评价及防治提供理论支持，具有很强的现实意义，因此，开展老滑坡变形预测模型构建具有重要的意义．

受隧道施工等因素影响，滑坡变形监测数据会含有一定的随机信息［9］，这会影响预测精度，且根据张明岳等［10］研究，变分模式分解具有良好的数据分解能力，能将岩土变形序列分解为若干模态，适用性已被验证，加之移动平均法能有效识别变形数据中的趋势变量，趋势位移提取能力也较强，因此，此两方法综合能有效实现滑坡变形数据分解，即将变形数据分解为趋势位移和随机位移．

完成数据分解后，先结合趋势位移特点，建议以双向长短期记忆为基础构建其预测模型［11］，通过猎食者算法确保其参数最优性；其次，随机位移不确定性、非线性特征显著，通过挖掘滑坡变数据变分模态与其之间的潜在关系是一个值得考虑的思路，基于此思路基础上构建了随机位移的多尺度预测模型［12］，且顾及BP神经网络［13］、支持向量机［14］在滑坡变形预测的中的普适性，再进一步提出以此两类方法具体实现随机位移预测．

综上，以隧道洞口段复活滑坡为分析实例，利用变分模式分解开展滑坡变形数据的模态识别，并结合移动平均法进行趋势位移提出，将滑坡变形数据分解为趋势位移和随机位移；在滑坡变形数据分解基础上，基于数据自掘性、多尺度识别思路，利用猎食者算法、双向长短期记忆BP神经网络、支持向量机等开展滑坡变形综合预测，以期实现滑坡变形的高精度预测，为其后续防治奠定基础．

1" 基本原理

利用变分模式分解（varational mode decomposition， VMD）开展滑坡变形数据分解处理，并结合移动平均法（moving average， MA）进行趋势位移提出，即将滑坡变形数据分解为趋势位移和随机位移；利用猎食者算法（hunter prey optimizer，HPO）和双向长短期记忆（bidirectional long short term memory， BiLSTM）构建出HPO-BiLSTM，并通过其实现趋势位移预测，再以变分模式分解的数据分解结果为基础，与随机位移构建多尺度分析，并以BP神经网络或支持向量机（support vector machine， SVM）实现随机位移的自掘性预测；将趋势位移预测结果与随机位移预测结果相加，所得值即为滑坡变形最终预测结果．

1.1" 各类基础模型的原理

1.1.1" 变分模式分解和移动平均法

滑坡地层结构本身具非均质特征，且隧道施工过程中的爆破、机械等均会对滑坡变形造成一定影响，主要表现为：滑坡变形非线性特征显著，侧面验证多方法构建本文预测模型的合理性；滑坡监测数据并不能代表其真实变形，即其数据含有一定的随机信息．因此，可将滑坡变形

监测数据Yt可表示为：

Yt=Qt+St，（1）

其中，St为随机位移，代表滑坡误差变形；Qt为趋势位移，代表滑坡真实变形.

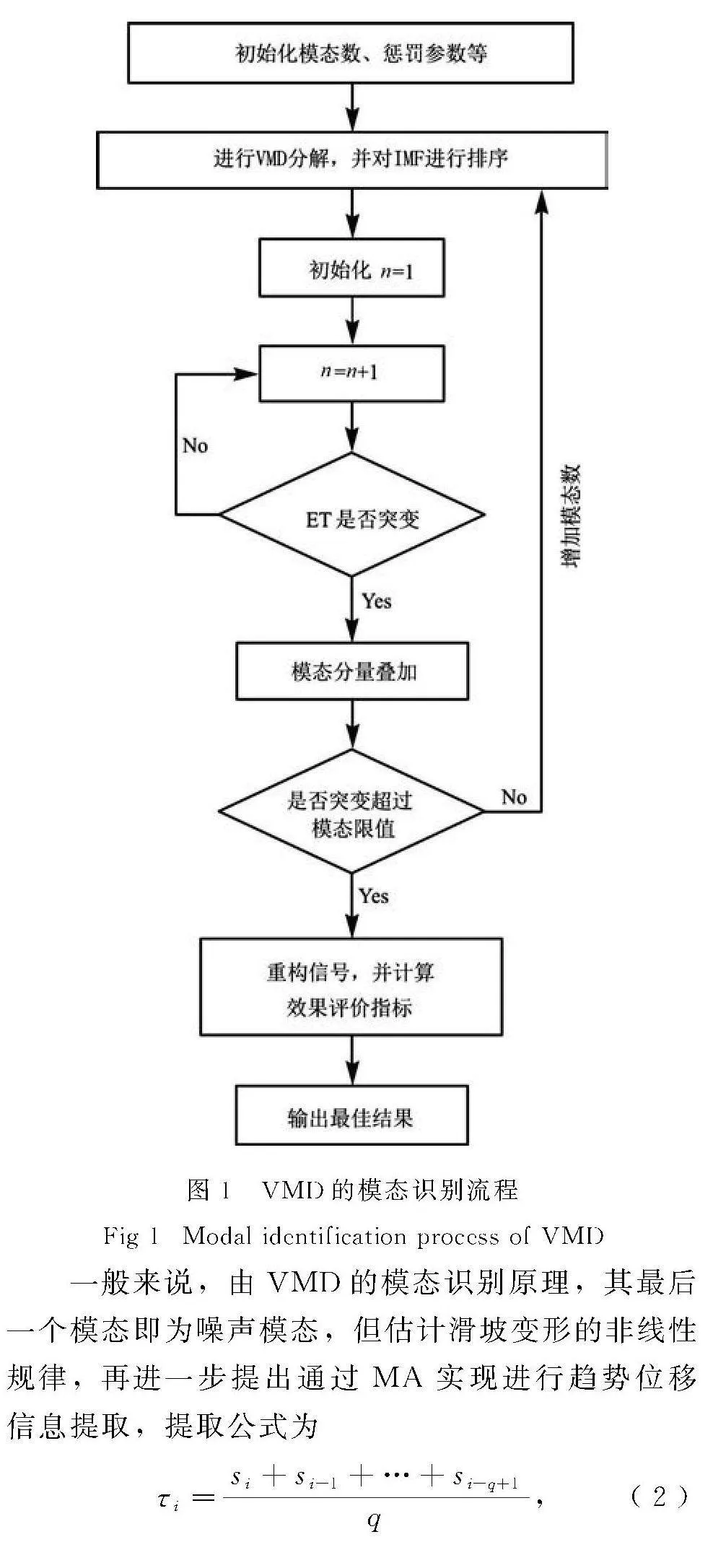
VMD是通过希尔伯特变换将变形序列转变为若干模态，适用于变形数据的分解处理，因此，引入VMD进行滑坡变形数据的模态识别，其思路为：先利用希尔伯特变换得到滑坡变形数据的模态函数，并计算器单侧频谱；将频谱转变为基频带，并估算其带宽实现模态约束性变分处理；将约束性变分处理过程再进一步转变为非约束性变分处理过程，形成VMD的模态识别流程见图1．

Fig 1Modal identification process of VMD

一般来说，由VMD的模态识别原理，其最后一个模态即为噪声模态，但估计滑坡变形的非线性规律，再进一步提出通过MA实现进行趋势位移信息提取，提取公式为

τi=si+si-1+…+si-q+1q，（2）

其中，τi为对应时刻的趋势位移观测值；si为对应时刻的累计位移观测值；q为移动周期

经过上述处理，将滑坡变形数据分解为了趋势位移和随机位移，并将dnSNR（降噪误差比）进行分解效果评价，公式为

dnSNR=10×lgPsPg，（3）

其中，Ps为Yt序列的功率；Pg为Qt序列的功率

由的计算原理，其dnSNR值越小，说明数据分解效果越优．

1.1.2" 趋势位移的预测模型

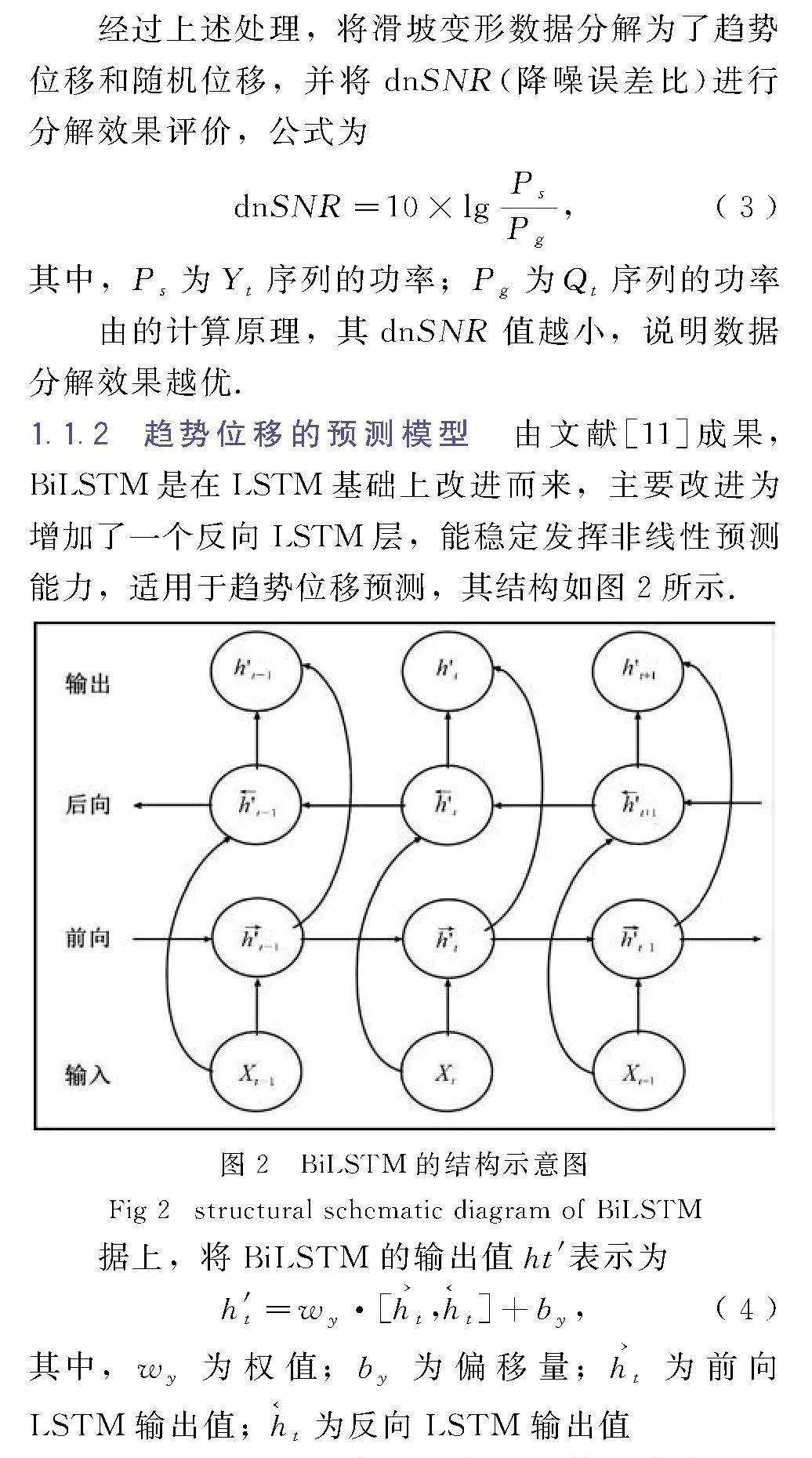
由文献［11］成果，BiLSTM是在LSTM基础上改进而来，主要改进为增加了一个反向LSTM层，能稳定发挥非线性预测能力，适用于趋势位移预测，其结构如图2所示．

Fig 2structural schematic diagram of BiLSTM

据上，将BiLSTM的输出值ht′表示为

h′t=wy·［t，t］+by，（4）

其中，wy为权值；by为偏移量；t为前向LSTM输出值；t为反向LSTM输出值

通过BiLSTM的使用可知，权值、偏移量是由模型随机产生，客观性欠缺，且考虑到HPO能模拟肉食动物的捕食过程，具有参数少、收敛速度快、寻优能力强等优点，再进一步引入HPO进行其参数优化处理．

由HPO原理，将其寻优过程介绍为

① 对HPO的初始参数进行设计，如将肉食动物个数设置为300头，最大寻优次数为600次，其他参数随机设置．

② 对动物个体的平衡参数进行计算，并在此基础上，进一步计算器自适应参数．

③ 对动物个体位置信息，并从新计算其自适应参数，若达到最优效果则停止寻优，输出结果即可；反之，继续寻优，直至达到最大迭代次数．

综上，HPO的最重要步骤是位置更新，其更新公式为：

xi（t+1）=xt（t）+0.56［2CZPpos-xi（t））+

（2（1-C）Zμ-xi（t））］，

R5lt;β;

Tpos+CZcos（2πR4）（Tpos-xi（t）），

R5≥β.（5）

其中，x（t），x（t+1）为相应节点处的位置；R5为0～1间的随机数；β为条件参数，将其值设定为0.15；Ppos为猎物位置；μ为所有位置的均值；R4为-1～1间的随机数；Z为自适应参数；C为平衡参数；Tpos为全局最优位置.

将滑坡趋势位移的预测模型设定为HPO-BiLSTM．

1.1.3" 随机位移的预测模型

滑坡变形的随机位移的波动特征显著，因此，其预测模型构建十分重要．为保证随机位移预测精度，从自掘性、多尺度特征入手，其一，滑坡变形影响因素较多，但各影响因素对变形贡献多少难以确定，因此，以其作为输入层是不合适的；不过值得指出的是，通过VMD将滑坡变形分解为了若干模态，不同模态与随机位移间存在潜在相关性，可通过自掘性发现不同模态与随机位移间关系是可行的．其二，以VMD分解的模态为基础，开展多尺度识别，构建出多类多尺度识别模型．

在前述自掘性、多尺度识别基础上，再进一步利用BP神经网络或SVM进行预测．

1）BP神经网络的预测过程

BP神经网络是一种常见的预测方法，具有较优的鲁棒性和泛化能力，非线性拟合能力较强，已被岩土领域的变形预测广泛应用，因此，适用于随机位移的预测处理．

BP神经网络的预测训练过程包括正、反向训练过程，其中，正向过程表示输入信息从输入层转入，经隐层变换，并由输出层输入，计算公式为

x′j=f1∑ni=1wijxj-Qj， 1≤j≤n，（6）

yk=f2∑mj=1wijx′j-Qk， 1≤k≤m.（7）

其中，xj为变形输入值；Qj，Qk为相应层间阈值；yk为变形输出值；x′j为隐层输出值；wij，wjk为相应层间连接权值；m为输出节点个数；n为隐层节点个数.

当正向传播不满足期望时，以Newton理论为基础，开展连接权值、阈值调整，变化量的公式为

ΔW=（JTJ+uI）-1JTE，（8）

其中，△W为相应调整参数的变化量；J为雅可比一阶偏导矩阵；I为迭代矩阵；E为误差矩阵.

在连接权值、阈值调整变化量计算基础上，再将反向传播过程中的相应连接权值、阈值表示为

W（t+1）=W（t）+ΔW，（9）

其中，W（t+1）为连接权值、阈值修正值；W（t）为连接权值、阈值的原参数值.

2）SVM的预测过程

SVM能在正则化原理基础上保证计算风险的最小化，具有较强的全局预测能力和泛化能力，对随机位移的预测能力强．训练函数表示为

yi=wφ（xi）+b，（10）

其中，yi为预测值；φ（xi）为映射函数；ω为权向向量；b为偏置向量.

按照SVM原理，需对预测过程进行最小化结构风险控制，其控制条件为

minΦ（ω，b，ξi，ξi*）=

12ω2+C∑li=1（ξi+ξi*，（11）

s.t.［（ωxi）+b］-yi≤ε+ξi，

i=1，2，…，n;

yi-［（ωxi）+b］≤ε+ξi*，

i=1，2，…，n;

ξi，ξi*≥0， i=1，2，…，n.（12）

其中，ε为超出误差；ξi，ξi*为松弛变量；C为惩罚因子.

在结构风险控制条件下，再将预测函数表示为

f（x）=∑li=1（αi-αi*）K（xi，xj）+b，（13）

其中，f（x）为变形预测值；l为训练集个数；K（xi，yj）为核函数；αi，αi*为拉格朗乘子

在随机位移变形预测过程中，利用BP神经网络、SVM进行多尺度条件下的变形预测，选取效果最优者作为随机位移的预测结果．

1.2" 预测模型的总体构建

在1.1节各类基础模型的原理介绍基础上，再将滑坡变形预测模型总体设计如图3所示．据图3，将预测流程进一步总结如下：

① 先利用VMD进行滑坡变形数据分解，此步骤包含两次同样的分解处理，先将数据分解1作为后续随机位移模型构建自掘性、多尺度识别的基础；再将数据分解2作为后续趋势位移、随机位移的基础．

② 通过MA法开展趋势位移的信息提取，将滑坡变形数据分解为趋势位移和随机位移．

③ 利用HPO-BiLSTM实现趋势位移的变形预测；进行滑坡分解模态间的自掘性信息分析，构建出多尺度识别模型，通过BP或SVM进行预测．

④ 将趋势位移预测结果与随机位移预测结果相加，所得值即为滑坡变形最终预测结果，即完成滑坡变形预测．

在预测过程中，提出以平均绝对百分误差（mean absolute percentage error，EMAP）开展预测模型的精度评价，计算公式为

EMAP=1N∑Nt=1Mt-mtMt，（14）

其中，N为验证集个数；Mt为实测值；mt为预测值.由EMAP的构建原理，其值越小，说明预测精度越高；反之，预测精度越低．同时，再引入训练时间Tt评价训练速度，其值越小，说明其训练过程较快．

2" 实例分析

2.1" 工程概况

滑坡位于隧道出口端，且隧道基本特征为：洞口段具中低山丘陵地貌，地形高程845.25～902.41 m，起伏相对较大；左线起、止里程ZK23+152～ZK26+664 m，长度为3 512 m，最大埋深约264.23 m；右线起、止里程ZK23+180～ZK26+672 m，长度为3 492 m，最大埋深约250.07 m．

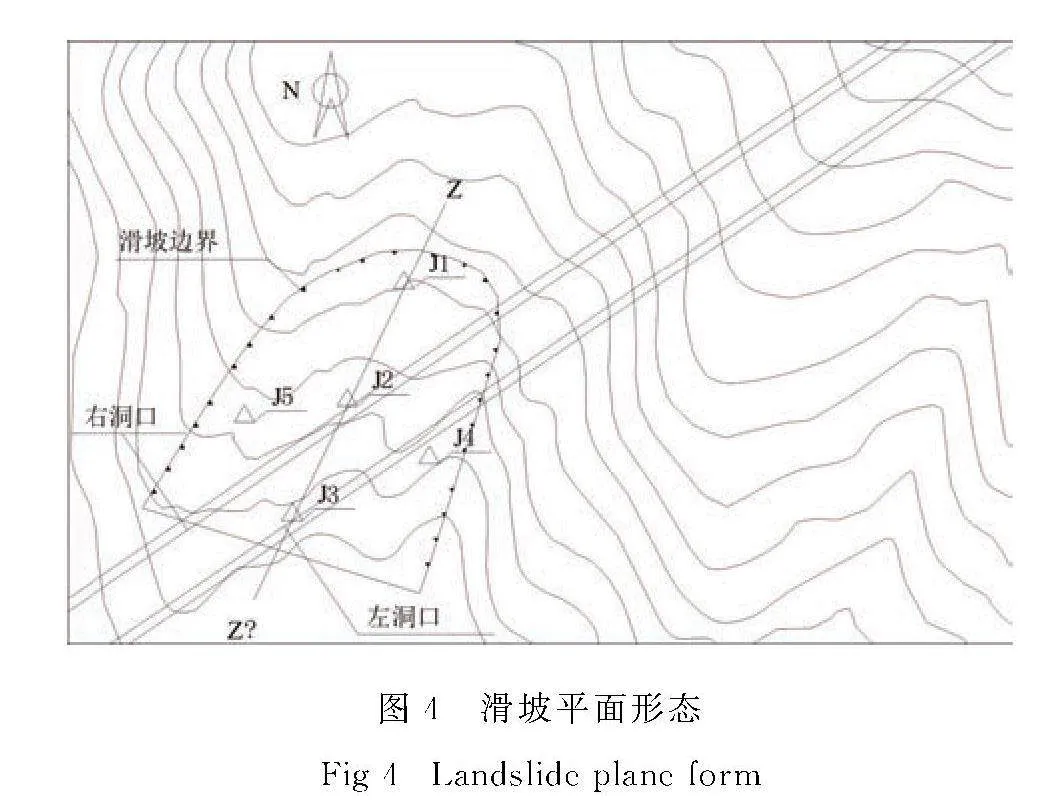
据现场调查，洞口滑坡属老滑坡，主要是由隧道洞口段施工诱发复活．滑坡平面呈“舌”状（图4），主滑方向为189°，纵向长度约200 m，横向宽度介于84～115 m，平均厚度约8.0 m，体积约18.31×104 m3，属中型土质滑坡．

据钻探成果，滑坡区地层特征如下：

滑体土．岩性为粉质黏土夹碎块石，紫红色，厚度介于5.7～12.5 m，平均厚度约8.0 m，可塑-硬塑状，稍湿，所处状态受降雨影响较大，并含有少量碎块石，含量一般介于5%～10%，粒径多处于5～15 cm，磨圆度较差，多为次棱角状．

滑带土．岩性为粉质黏土，紫红色，厚度介于13～24 cm，可塑状，稍湿，遇水易软化，含有少量角砾，含量一般少于5%，多为次圆状．

滑床．岩性为板岩，灰黑色，强-中风化，原岩结构基本破坏，节理裂隙发育，多为碎裂结构，完整性较差，局部裂隙由方解石充填，抗压强度较

小，属软岩．

2.2" 滑坡区变形特征分析

结合调查资料，滑坡区变形主要体现在两方面，其一，是隧道洞内支护结构变形；其二，是滑坡地表变形．

1）隧道洞内变形特征

滑坡区内隧道洞内变形主要表现为初支结构变形，经统计，在滑坡段的洞内初支变形介于94.25～206.71 mm，绝大部分均大于预留变形量（120 mm），因此，此段洞内表现为初支超限．

2）滑坡地表变形特征

地表变形主要表现为洞口局部出现地表坍塌及地表裂缝．地表坍塌主要发生一次，形成塌方洞口长度2.9 m，宽度2.2 m，深度约1.9 m．地表裂缝主要发育有3条，特征为：

裂缝1延伸长度约25.8 m，宽度6.3～17.1 cm，可见深度最大约1.3 m，无明显下错，无闭合特征．

裂缝2延伸长度约20.4 m，宽度10.6～15.8 cm，可见深度最大约1.1 m，局部下错5.3～9.7 cm，局部位置有闭合，但不显著．

裂缝3延伸长度约31.8 m，宽度8.4～21.5 cm，可见深度最大约1.5 m，局部下错8.5～13.7 cm，暂无闭合特征．

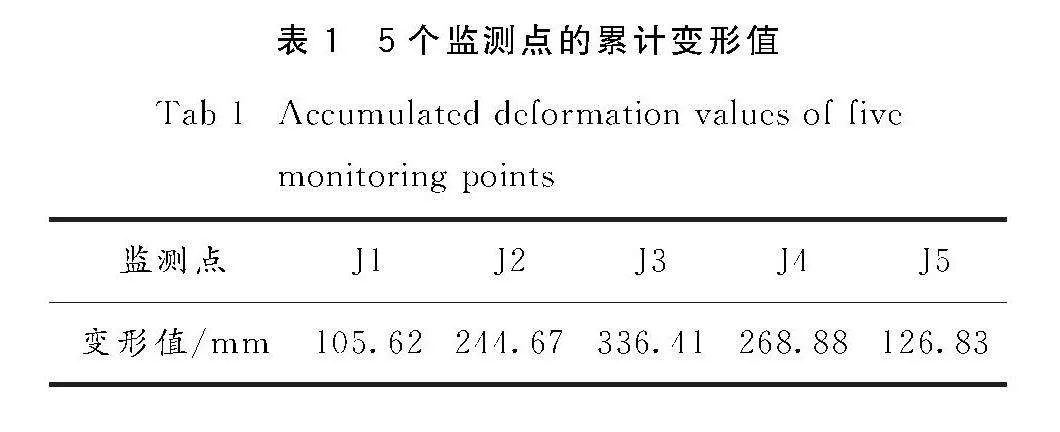
在发现洞口滑坡复活后，于地表布设了5个监测点（图4），按照4天1次的频率统计，共计统计得到30期变形数据（监测时间为2022年4月13日至2022年8月11日）．经统计，5个监测点的累计变形值见表1．据表1，地表变形范围介于105.62～336.67 mm，总体变形值偏大．

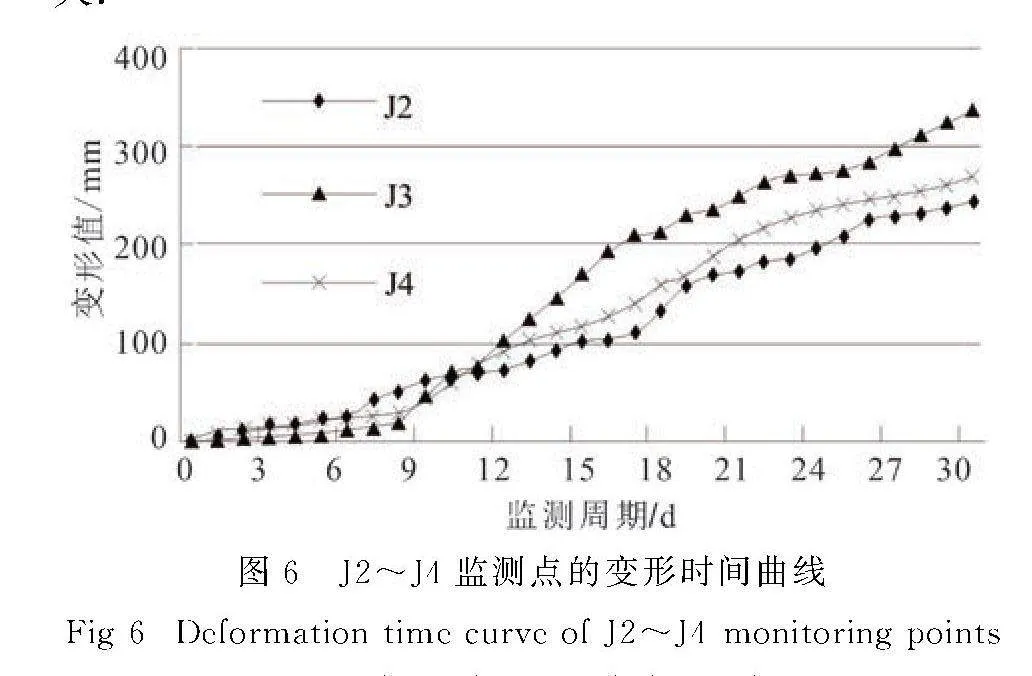
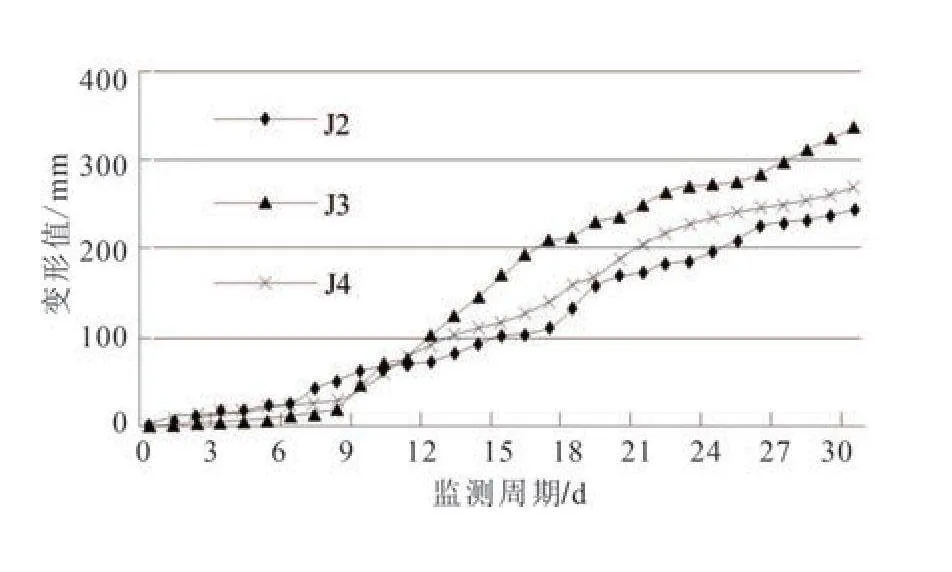
限于篇幅，提出对3个变形最大的监测点进行分析，即以J2～J4监测点作为后续分析的数据来源.通过统计，J2～J4监测点的变形曲线见图6．据图6，J2～J4监测点的累计变形规律表现为：总体增加，且前期增加速率相对较厚，中、后相对略大．

J2～J4监测点的变形速率特征参数为：J2的变形速率范围为0.47～26.51 mm·d-1，平均值为8.16 mm·d-1；J3的变形速率范围为0.80～26.60 mm·d-1，平均值为11.21 mm·d-1；J4的变形速率范围为0.49～20.97mm·d-1，平均值为8.96 mm·d-1．

2.3" 滑坡变形预测结果

按照图3的预测思路，先利用VMD开展滑坡变形数据的分解处理，且为对比其分解效果，再引入sym小波、db小波进行类似分解处理，得三者的结果为：VMD的dnSNR值为18.26，sym小波的dnSNR值为31.47，db小波的dnSNR值为35.22．VMD的分解效果明显优于其他两类方法，充分验证其分解能力．

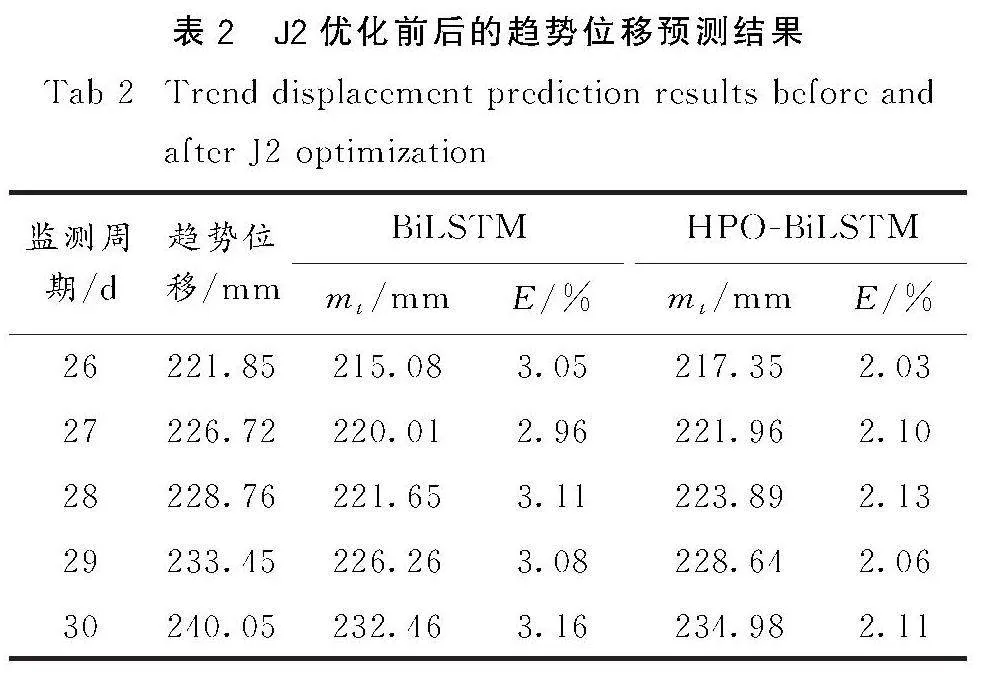
再利用MA法进行趋势信息提取，并以J2为例，详述对比不同步骤的预测效果．经计算，得到J2优化前后的趋势位移预测结果见表2．

在26～30期的预测结果中，HPO-BiLSTM的E值均不同程度的少于BiLSTM的E值，且HPO-BiLSTM的EMAP值为2.09%，Tt值为182.66 ms；BiLSTM的EMAP值为3.07%，Tt值为265.71 ms．对比来说，经HPO的优化处理，能有效提高J2趋势位移的预测精度及训练速度．

通过VMD分解处理，将滑坡变形数据分解为14种模态，即IMF-IMF14，并在J2随机位移的多尺度识别中共计设计了10种多尺度模型，其输入层为随机确定的分解模态，输出层均是对应随机位移，具体设计为多尺度模型1的输入模态为IMF1，IMF3，IMF6，IMF9，IMF10，IMF12；多尺度模型2的输入模态为IMF1，IMF2，IMF3，IMF8，IMF10，IMF11；多尺度模型3的输入模态为IMF2，IMF3，IMF5，IMF6，IMF11，IMF12；多尺度模型4的输入模态为IMF1，IMF2，IMF7，IMF10，IMF11，IMF12；多尺度模型5的输入模态为IMF1，IMF2，IMF3，IMF6，IMF7，IMF9，IMF10，IMF12；多尺度模型6的输入模态为IMF2，IMF3，IMF5，IMF6，IMF7，IMF9，IMF11，IMF12；多尺度模型7的输入模态为IMF1，IMF2，IMF4，IMF5，IMF7，IMF9，IMF10，IMF14；多尺度模型8的输入模态为IMF1，IMF2，IMF4，IMF5，IMF6，IMF7，IMF9，IMF10，IMF14；多尺度模型9的输入模态为IMF1，IMF3，IMF4，IMF5，IMF6，IMF8，IMF9，IMF12，IMF14；多尺度模型10的输入模态为IMF1，IMF2，IMF4，IMF5，IMF6，IMF7，IMF9，IMF10，IMF11，IMF12，IMF14．

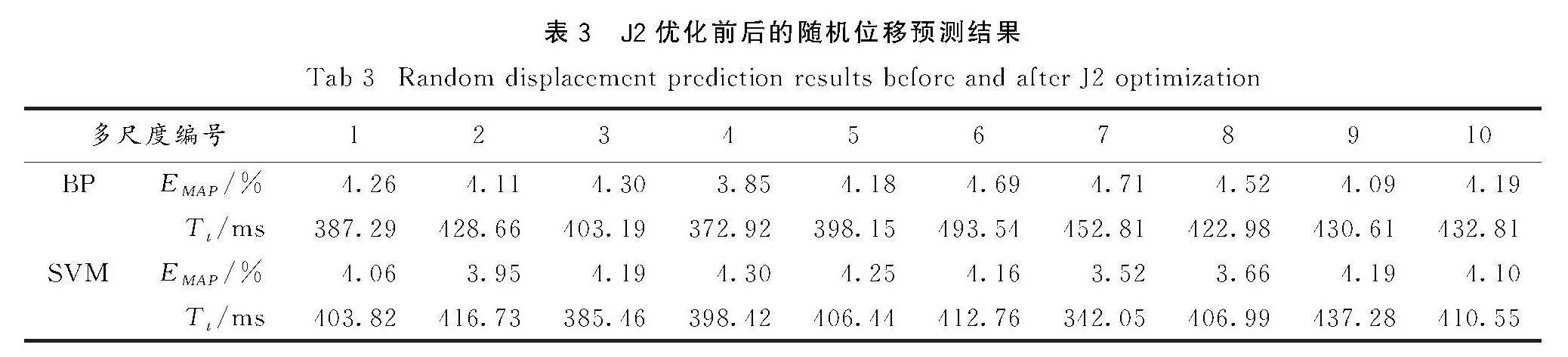
在多尺度模型设计基础上，以BP神经网络、SVM进行相应预测，所得结果见表3．两类模型在不同尺度条件下预测结果存在明显差异，其中，在相同尺度条件下，两类模型的预测结果对比，得出BP神经网络的EMAP值和Tt值均明显大于SVM的EMAP值和Tt值，说明SVM在滑坡随机位移中的预测效果更优；在SVM的预测结果中，对比10种尺度条件下的预测结果，得出SVM在多尺度7条件下的预测效果相对最优，因此，以此尺度组成作为随机位移的预测模型．

经统计，J2的最终预测结果见表4.J2最终预测结果的E值范围介于1.92%～2.06%，EMAP值为2.01%，Tt值为162.45 ms，预测效果明显较优，充分验证了此文预测思路具有较优的预测效果，合理性显著．再利用图3预测思路进行J2～J4

监测点的变形预测，结果见表5．J2的EMAP值为2.01%，Tt值为162.45 ms；J3的EMAP值为2.05%，Tt值为185.45 ms；J4的EMAP值为2.02%，Tt值为168.45 ms．通过预测结果对比，其预测精度、训练速度相当，充分说明此文预测模型不仅具有较优的预测精度，还具较强的稳定性．

由3个监测点在31～34期的预测结果可知，三者的后续变形仍会进一步增加，且增加速率较大，无收敛趋势，即滑坡地表变形还会进一步增

加，需尽快开展防治研究．为进一步佐证预测思路的合理性，再利用极限学习机、灰色GM（1，1）进行同样预测，所得结果见表6．据表6，在相应监测点调间隙，本文预测模型的EMAP、Tt值明显小于极限学习机、灰色GM（1，1）的EMAP、Tt值，且本文预测模型的EMAP均值为2.03%，Tt均值为172.12 ms；极限学习机的EMAP均值为3.12%，Tt均值为328.20 ms；灰色GM（1，1）的EMAP均值为3.23%，Tt均值为324.63 ms．三类模型对比来说，本文预测模型相较传统预测模型的预测能力更强．

通过上述，本文预测模型能有效实现滑坡变形的高精度预测，为滑坡变形发展规律奠定了理论基础，值得进一步推广应用研究．

3" 结论

通过前述研究成果，所得主要结论为：

1）隧道洞口段地质条件较差，受施工影响，易复活老滑坡，且滑坡变形直接关系其稳定性，因此，开展洞口滑坡变形预测研究是十分必要的．

2）为确保预测精度，通过多类模型的综合构建是必要的，其中，VMD能有效实现变形数据的分解处理，其分解效果明显优于sym小波、db小波的分解效果；HPO-BiLSTM能有效实现滑坡趋势位移的变形预测，且HPO的参数寻优对预测精度的提高较大；在随机位移预测中，自掘性、多尺度分析是十分必要，并经研究，得出BP神经网络或SVM在多尺度条件下的预测效果存在一定差异，侧面也说明利用多尺度识别模型实现随机位移预测是可行的．

3）通过本文预测，3个监测点的EMAP、Tt值均较小，具有较高的预测精度及训练速度，再与极限学习机、灰色GM（1，1）的预测结果对比，具有更优的预测效果．

参考文献：

［1］" 赵金，文丽娜，吴红刚，等．隧道-洞口滑坡平行体系受力变形模式与计算方法研究［J］.现代隧道技术，2022，59（2）：53．

［2］" 尹川，王剑非，周文皎，等．隧道正交穿越滑坡体的变形特征及控制技术探讨［J］.铁道建筑，2021，61（6）：59．

［3］" 刘传利，童建军．滑坡-隧道斜交体系稳定性案例分析及综合治理——以云南大关至永善高速公路椿坪2号隧道出口段为例［J］.隧道建设（中英文），2022，42（S2）：161．

［4］" 李洋溢，何克扬．大跨度隧道洞口滑坡形成机制及处治方案研究［J］.公路，2022，67（9）：464．

［5］" 刘传利，桂登斌．高速公路滑坡地段隧道倾斜进洞方案研究［J］.现代隧道技术，2021，58（S1）：207．

［6］" 李广林，王亮，郭毅．浅谈隧道洞口仰坡滑坡成因及综合治理措施［J］.现代隧道技术，2020，57（S1）：1147．

［7］" WANG Y X，LI S Y，LI B．Deformation prediction of cihaxia landslide using InSAR and deep learning［J］.Water，2022，14（24）：3990．

［8］" LI H S，WU Z L，CHEN J J，et al．Multiple data-driven approach for predicting landslide deformation［J］.Landslides，2020，17（3）：709．

［9］" 赵淑敏．基于信息分解条件的滑坡变形预测［J］.水土保持通报，2021，41（3）：181．

［10］" 张明岳，李丽敏，温宗周．基于变分模态分解和双向长短时记忆神经网络模型的滑坡位移预测［J］.山地学报，2021，39（6）：855．

［11］" 刘相杰，刘小生，张龙威．基于VMD-HPO-BiLSTM的大坝变形预测［J］.大地测量与地球动力学，2023，43（8）：851．

［12］" 熊超，孙红月．基于多因素-多尺度分析的阶跃型滑坡位移预测［J］.吉林大学学报（地球科学版），2023，53（4）：1175．

［13］" 曹小燕，满新耀，汪继平，等．基于鸟群优化BP神经网络的滑坡处治后变形预测［J］.测绘通报，2023（5）：27．

［14］" 宁波，刘玉健，王安东．巨型古滑坡的稳定性评价及发展趋势分析［J］.大地测量与地球动力学，2022，42（5）：515．

（责任编辑" 武维宁）