基于变分模态分解和改进频率增强分解变压器的有色金属价格预测

摘要：准确预测有色金属价格对于决策者、投资者和研究人员具有重要意义.为了提高预测精度，文中提出了一种新型混合预测模型，称为（EVMD-ICEEMDAN-RFEDformer， EIRF）.首先，使用变分模态分解（variational mode decomposition，VMD）将原始价格分解为多个分量，同时使用改进的蚁狮搜索算法（modified ant lion optimization，MALO）对VMD的两个参数进行优化.其次，采用改进的带有自适应噪声的完全集成经验模式分解（improved complete ensemble empirical mode decomposition with adaptive noise，ICEEMDAN）进一步分解VMD产生的残差序列，从中提取有价值的信息.然后将所有分解的子序列输入到改进的频率增强分解变压器（reinforced frequency enhanced decomposition transformer，RFEDformer）中.最后，合并RFEDformer的预测并得出最终结果.为了验证模型的可靠性，文中利用了伦敦金属交易所的锡、铜和镍价格数据制定了3个不同的实验，并与12个对比模型进行了比较.结果表明混合模型在3个数据集上都取得了良好的性能.

关键词：有色金属价格预测;蚁狮优化算法;二次分解;RFEDformer模型;Sophia优化器;IKMSE损失函数

中图分类号：TM 41;TP 18""" 文献标志码：A""" 文章编号：1001-988Ⅹ（2025）01-0051-10

DOI：10.16783/j.cnki.nwnuz.2025.01.010

收稿日期：20240320;修改稿收到日期：20240810

基金项目：国家自然科学基金资助项目（42371377）

作者简介：王瑞（1999—），女，甘肃定西人，硕士研究生.主要研究方向为时间序列与神经网络预测.

Email：3074882389@qq.com

*通信联系人，男，教授，博士.主要研究方向为数据同化和时间序列.

Email：baiyulong@nwnu.edu.cn

Nonferrous metal price prediction based on variational mode

decomposition and reinforced frequency enhanced

decomposition transformer

WANG Rui，SONG Qi，LIU Wen-hui，BAI Yu-long

（College of Physics and Electronic Engineering，Northwest Normal University，Lanzhou 730070，Gansu，China）

Abstract：Accurately forecasting the prices of non-ferrous metals holds significant importance for decision-makers，investors，and researchers.To enhance prediction accuracy，this study introduces a novel hybrid prediction model called EIRF（EVMD-ICEEMDAN-RFEDformer）.Initially，the

original price undergoes decomposition into multiple components using variational mode

decomposition（VMD），and the two parameters of VMD are optimized by modified ant lion search algorithm（MALO）.Secondly，the improved fully integrated empirical mode decomposition with adaptive noise（ICEEMDAN） is applied to further break down the residual sequence produced by VMD，extracting valuable information from it.Finally，the forecasts from RFEDformer are combined to yield the final results.To validate the models reliability，three experiments were conducted using price data for tin，copper，and nickel from the London Metal Exchange，comparing its performance with 12 benchmark models.The results indicate that the hybrid model demonstrates strong performance across all three datasets.

Key words：non-ferrous metal price forecasting;ant lion optimization algorithm;quadratic decomposition;RFEDformer model;Sophia optimizer;IKMSE loss function

有色金属在国民经济和人民生活中发挥着重要作用，广泛应用于机械制造、能源、化工制造、建筑等众多领域［1］.随着社会的进步和全球通胀的加剧，贵金属投资已成为对抗通胀、对冲风险、保值的理想选择［2］.同时，有色金属价格的涨跌影响着全球经济和企业的经营业绩.智利和赞比亚等国家收入严重依赖有色金属出口，使其经济容易受到价格波动的影响［3］.对于矿业公司来说，金属价格在投资中会影响项目估值［4］.然而，有色金属具有商业和金融特性，其价格不仅受供求和生产成本的影响，还受到美元汇率等因素的影响.这些不同的因素相互交织、相互关联，导致有色金属价格更加剧烈的波动［5］.因此，有效地对有色金属价格波动进行建模并预测其趋势，对于更好地预测大宗商品价格、合理配置资源、及时调整经营策略以及提高价格稳定性具有重要意义.

1" 材料与方法

1.1" 研究现状

1.1.1" 基本模型

在金属价格预测领域，基本模型分为两大类：传统模型和人工智能模型.传统模型有ARIMA、GARCH，以及霍尔特指数平滑法［6］.例如，Dooley等［7］采用ARIMA和滞后远期价格模型来预测锌和铅价格，Rubaszek等［8］利用均值回归模型来预测铝、铜、镍和锌的价格.虽然这些技术在金融时间序列中得到了广泛的应用，但预测有色金属价格需要大量的多元数据集.传统经济模型对非线性长期时间序列的预测能力往往不稳定.

近年来，人工智能模型的开发引起了诸多学者浓厚的兴趣.刘等［9］使用基于决策树的机器学习算法来预测铜价.然而，人工智能模型通常有很多超参数需要调整.为了克服这一缺点，一些学者结合元启发式算法来优化关键参数.罗等［10］开发了一种基于GA优化的LSTM和纠错策略的多步铜价预测架构.此外，有些研究人员合并各种单独的模型来预测有色金属价格.何等［1］利用IVMD，WPD，ARIMA，IELM和其他方法，引入了一种新颖的有色金属价格混合预测框架.然而，混合模型的整体复杂度较高，导致模型的训练成本增加.为了解决这些问题，一些学者对价格序列进行了分解.黄等［11］使用Prophet模型、ICEEMDAN和具有多模型优化误差修正的混合模型预测了锌、铝、铜和黄金的价格.赵等［12］引入了SSA优化的VMD和LSTM的混合价格预测模型来分析金属价格特征.孙等［13］提出了一种集成ICEMDAN，EMD，CSSA和KELM的预测模型来预测原油价格.这些研究表明，二次分解还可以增强模型的预测有效性.然而，在分解过程中，原始数据会产生一些残差，尤其是使用简单的分解方法时，无法完全捕捉数据的复杂性和变化.在之前的研究中，这个残差序列经常被忽视.因此，本文使用ICEEMDAN对VMD分解产生的残差进一步分解.

1.1.2" 变压器模型

在时间序列预测领域，随着计算资源的不断增加，通过编码和解码注意力层开发的Transformer模型已得到广泛应用［14］.然而，Transformer在处理长序列时计算复杂度和内存消耗较高，不能直接应用于长期时间序列预测［15］.为了解决这些问题，田等［16］通过将Transformer与季节性趋势分解方法相结合，提出了FEDformer.这种方法优先考虑频域内数据的低阶细节，在众多数据集中产生了较好的结果.在此基础上，文中提出了一种改进的RFEDformer，通过洞察更深入的频域范围，为预测有色金属价格提供新的研究视角.

1.1.3" 主要贡献和创新点

文中引入了一种基于数据预处理和RFEDformer的有色金属价格预测模型，命名为EIRF.其创新点主要有3方面：

1）提出了一种提高VMD自适应能力的新方法MALO［17］，通过结合Chebyshev混沌映射、差分变异扰动和黄金正弦策略，同时优化分解水平K和惩罚因子α.

2）提出了一种RFEDformer神经网络模型.将线性层整合到Transformer的前馈部分，并引入Leaky-relu激活函数创建MLP.对于反馈部分，采用了新颖的二阶截断随机优化器Sophia［18］和损失函数IKMSE［19］.

3）将第一次分解生成的残差序列进行二次分解，进一步提取残差中的信息.同时，引入新的混合模型来预测有色金属价格.

1.2" 方法论

1.2.1" 改进的蚁狮优化算法（MALO）

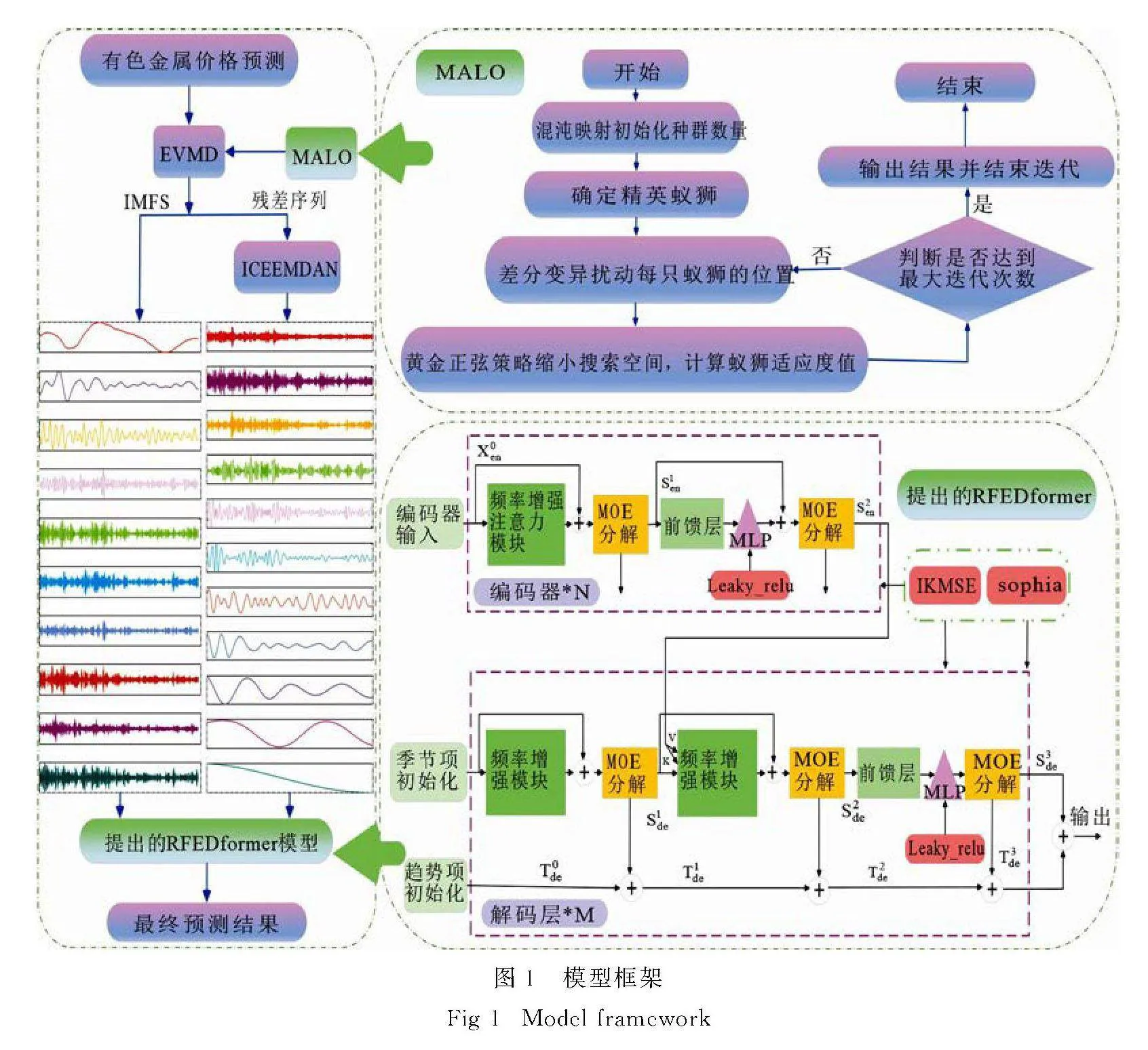
虽然ALO在某些方面优于GA、PSO、GWO、DA和PSO［20］，但是收敛缓慢并且容易陷入局部最优.因此，文中改进了ALO算法，结合Chebyshev混沌映射、差分变异扰动和黄金正弦策略.算法的简要流程如图 1所示.

首先，使用Chebyshev混沌图［21］初始化种群，保证解的多样性.然后，将参考文献［22］中描述的差分变异技术融入原始算法，以增强其跳出局部最小值的能力.最后，在每次迭代位置更新后，使用黄金正弦策略［23］来缩小搜索空间以逼近算法的最优解.

1.2.2" 变分模态分解（VMD）

VMD方法首先由Dragomiretskiy和Zosso提出.VMD的实现步骤如下：① 利用希尔伯特变换对原始信号进行处理，得到解析信号.② 分析这些信号并计算它们的单侧频谱.③ 将单侧频谱乘以相应的中心频率，将其调制到基带.④ 计算解调信号的梯度范数并估计每种模式的信号带宽.⑤ 对这些步骤进行约束变分处理.具体内容参考文献［24］.

1.2.3" 改进的带有自适应噪声的完全集成经验模态分解（ICEEMDAN）

许多研究者对信号分解技术进行了大量研究.CEEMDAN是EEMD的重要进步，它通过向每个IMF分量引入正负白噪声来解决模态混叠问题.在此基础上，Colominas等［25］引入了ICEEMDAN信号处理方法，该方法与CEEMDAN的不同之处在于在分解过程中直接结合高斯白噪声.ICEEMDAN算法的详细分解步骤参考文献［26］.

1.2.4" 提出的RFEDformer模型

虽然Transformer模型显著提高了长期序列的预测水平，但它们不仅计算成本较高，更重要的是无法捕捉时间序列的整体趋势.为了解决这些问题，RFEDformer将Transformer与季节趋势分解方法［27］相结合，主要包括典型的编码器-解码器架构.RFEDformer模型配置如图 1所示.

1）编码器和解码器.

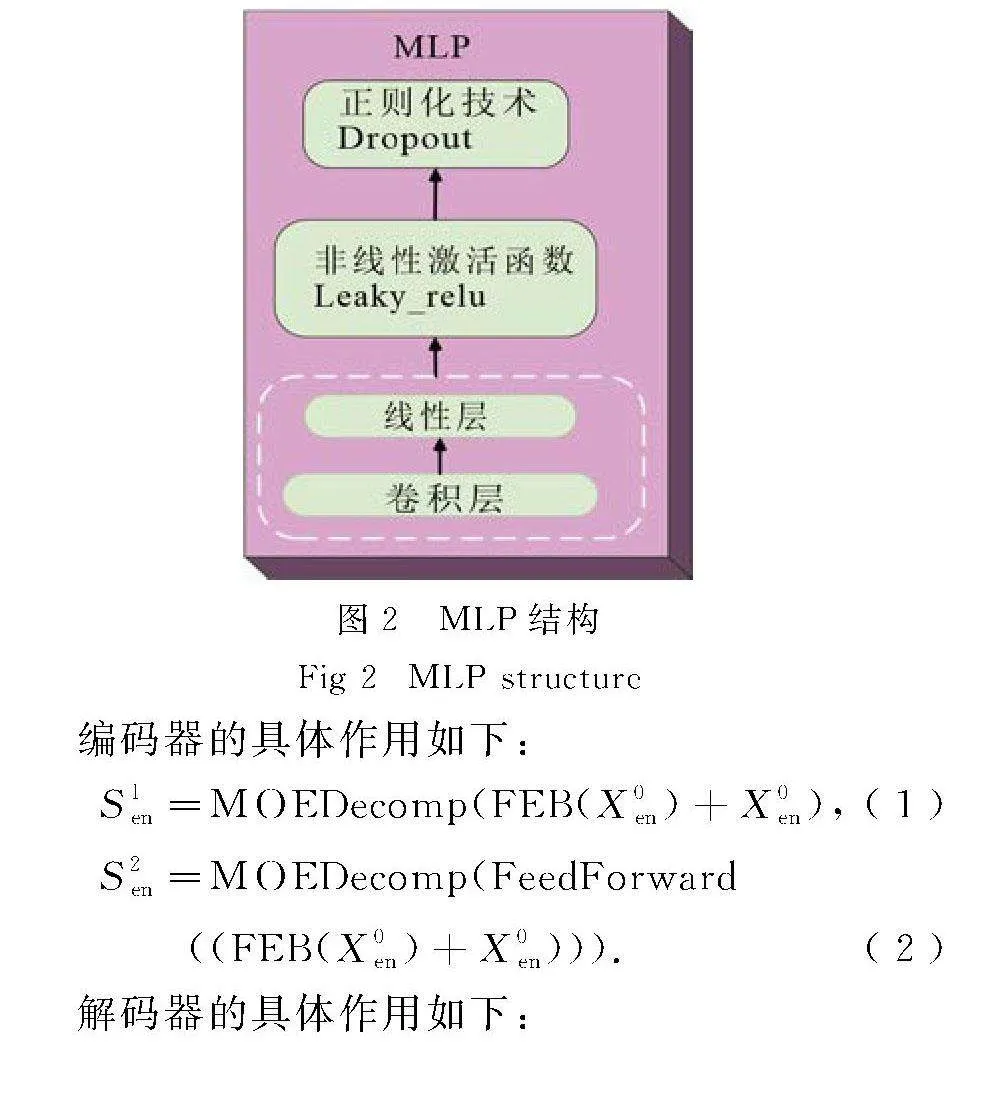
在编码器中，两个MOE分解层将长期价格序列分解为季节项和趋势项.趋势项保持不变，而季节项则在下一层进一步学习，然后返回解码器层.解码器的输入受到3个MOE分解层的影响，每个层同样分为趋势项和季节项两部分.趋势项保持不变，而季节项被转移到下一个模块持续学习.为了进一步提高模型的信息提取能力，在前馈模块中添加了一层MLP，在反馈层中添加了两层MLP.MLP的结构如图 2所示.最后将所有趋势项和季节项相加，还原金属价格序列.

编码器的具体作用如下：

S1en=MOEDecomp（FEB（X0en）+X0en），（1）

S2en=MOEDecomp（FeedForward

（（FEB（X0en）+X0en）））.（2）

解码器的具体作用如下：

S1dn，T1dn=MOEDecomp（FEB（X0dn）+X0dn），（3）

S2dn，T2dn=MOEDecomp（FEA

（S1de，LayerNorm（S2en）+S1de）），（4）

S3dn，T3dn=MOEDecomp

（FeedForward（S2de）+S2en）.（5）

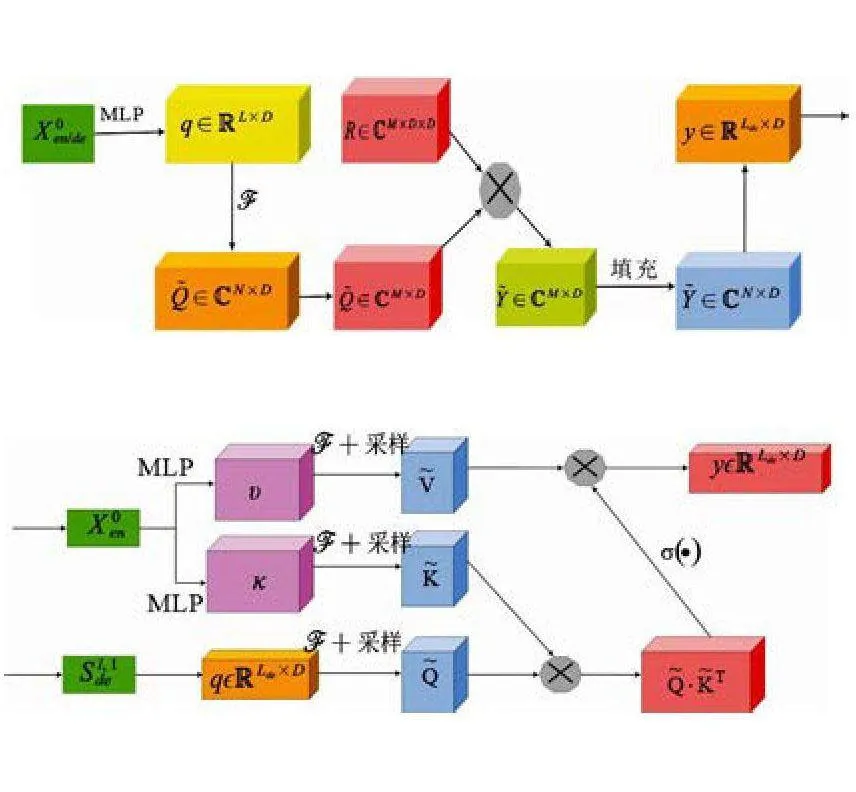
解码器对全连接层的可学习参数与傅里叶变换生成的频率特征进行点乘.频率增强模块的关键步骤如图3所示.

MOE分解模块采用不同大小的平均滤波器从输入信号中提取大量趋势元素.然后生成一组与数据相关的权重，并将这些元素整合起来形成最终的趋势线.该模块将金属价格序列分解为季节（S）和趋势（T）项，并在迭代过程中多次重复该过程［27］.

频率增强注意力模块的目的是促进编码器和解码器之间的通信，从而通过理解信号分量之间的内在联系来增强模型的预测和泛化能力.关键步骤如图4所示.

频率增强注意力模块的概述如下：

=Select（F（q）），（6）

=Select（F（k）），（7）

=Select（F（v）），（8）

FEA-f（q，k，v）=

F-1（Padding（σ·R）·）.（9）

其中q，k，v分别表示查询、键和值，σ（·）为激活函数.

2）优化器和损失函数.

Adam［28］及其变体是目前最流行的优化器之一，但它们通常会导致大量计算开销.为了解决这个问题，刘等［18］提出了一种称为Sophia的二阶截断随机优化器.与主流优化器相比，Sophia大大减少了训练时间和成本.

在时间步t上，Sophia用θt来表示参数.在每个步长下，从数据中采样一个小批量，计算该小批量的损失并用q表示.gt表示梯度，gt=Lt（θt）.令mt为EMA的梯度，则更新后的分子为mt←β1mt-1+（1-β1）gt.Sophia使用基于对角线Hessian的前提条件，直接根据参数维度的曲率调整大小.为了减少开销，文中每k步仅估计一次Hessian矩阵（在实现中k=10）.在时间步t上，估计器返回Hessian对角线的t估计.EMA每k步更新一次，对角Hessian估计规则更新为

ht=β2ht-k+（1-β2）t，

if t mod k=1; else ht=ht-1.（10）

MSE是时间序列中常见的损失函数.但由于其对异常值缺乏鲁棒性，难以准确评估有色金属价格的非线性特征.因此，Hong等［29］引入了一种新颖的IKMSE损失函数来桥接线性回归和内核方法.

IKMSE损失函数的表达式如下：

W=α∑Nt=1（1-e-（yt-t）2，（11）

R=（1-α）∑Nt=1max-12（yt-t），

12（yt-t），（12）

LWK（yt，t）=1N（W+R）.（13）

其中，α∈［0，1］为权重系数；yt为实际数据值，t为预测值.

2" 结果与讨论

2.1" 数据集描述

文中使用的有色金属数据集来自伦敦金属交易所（LME：https：//www.lme.com/Metals/Non-ferrous），用3种有色金属价格数据集（锡， 铜和镍）来验证文中提出的方法.每个数据集都以6∶2∶2的比例划分为训练、验证和测试子集.表1显示了数据集的具体特征.

2.2" 评价指标

本文用均方根误差（RMSE）、平均绝对百分比误差（MAPE）、平均绝对误差（MAE）和确定系数（R2）评估EIRF的预测性能，具体表达式为：

RMSE=1n∑nt=1（yt-t）2，（14）

MAPE=1n∑nt=1yt-yt，（15）

MAE=1n∑nt=1yt-，（16）

R2=1-∑nt=1（yt-）2∑nt=1（yt-）2.（17）

其中yt表示实际数据值，t表示预测值，可表示yt（t=1，2，…，n）的平均值.

2.3" 实验1：单模型对比实验

单模型比较的目的是将EIRF与5个基准模型比较，表2为实验中各模型的名称缩写.表3给出了每个模型的参数设置.

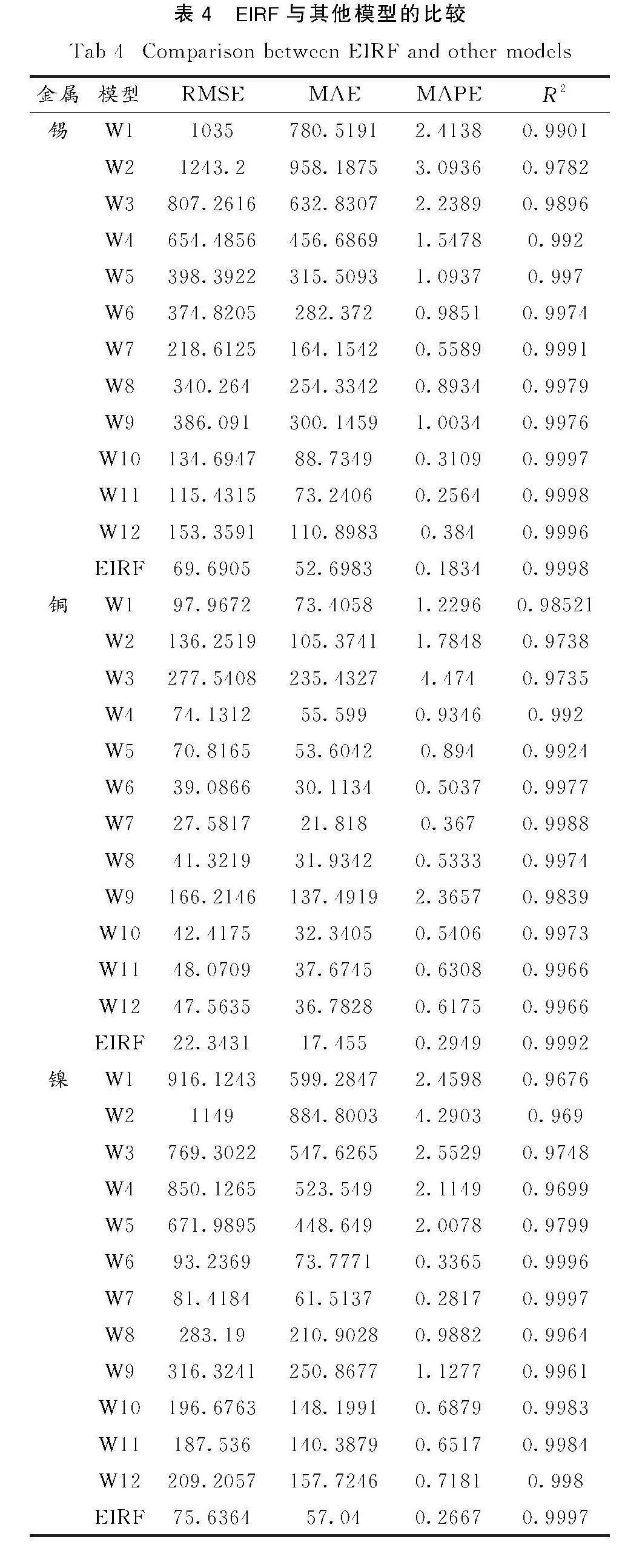
从表4和图5可以看出，EIRF在3个数据集上都取得了最好的预测结果.可以看出FEDformer和RFEDformer之间存在显著区别，证明了合并MLP层、优化损失函数和选择优化器的有效性.同时，EIRF的预测结果优于RFEDformer，充分说明了分解预测的重要性.

2.4" 实验2：混合模型的比较

实验1的结果表明，使用单一模型不能达到高精度预测目的.为了提高模型的预测性能，文中对初始序列和第1次分解产生的误差进行分解.

混合模型的对比结果如图 6和表 4所示.以锡为例，二次分解后Crossformer的预测指标RMSE，MAE，MAPE和R2分别提高了421.1706，332.6848，1.2355和0.008.FEDformer二次分解后的预测指标RMSE，MAE，MAPE和R2分别提高了314.2216，202.3527，0.6544和0.0059，进一步增强了FEDformer的预测效果.同时，对比一次分解后RFEDformer和EIRF的预测效果，发现后者的预测指标较前者提高了305.13，229.6737，0.8017和0.0024.这一结果再次证实了二次分解的必要性.

2.5" 实验3：消融实验

消融实验是通过去除或改变系统的某些部分来研究其功能的实验方法.为了进一步证实EIRF的有效性，我们控制了RFEDformer内部的部分变量.

在图7和表4中，以锡为例，EIRF显著提高了FEDformer的性能指标.与仅专注于优化MLP层和损失函数的FEDformer设置相比，EIRF将这些指标分别提高了65.0042，36.0366，0.1275和0.0001.同样，与仅专注于优化优化器和损失函数的设置相比，EIRF将这些指标分别提高了45.741，20.5423，0.073和0.0001.此外，与仅优化MLP层和优化器的设置相比，EIRF表现显著，RMSE，MAE，MAPE和R2分别增加了83.6686，58.2，0.2006和0.0002.每个变量都有助于改进预测结果，突出了增加MLP层深度和引入IKMSE和Sophia策略的有效性.

2.6" DM检测

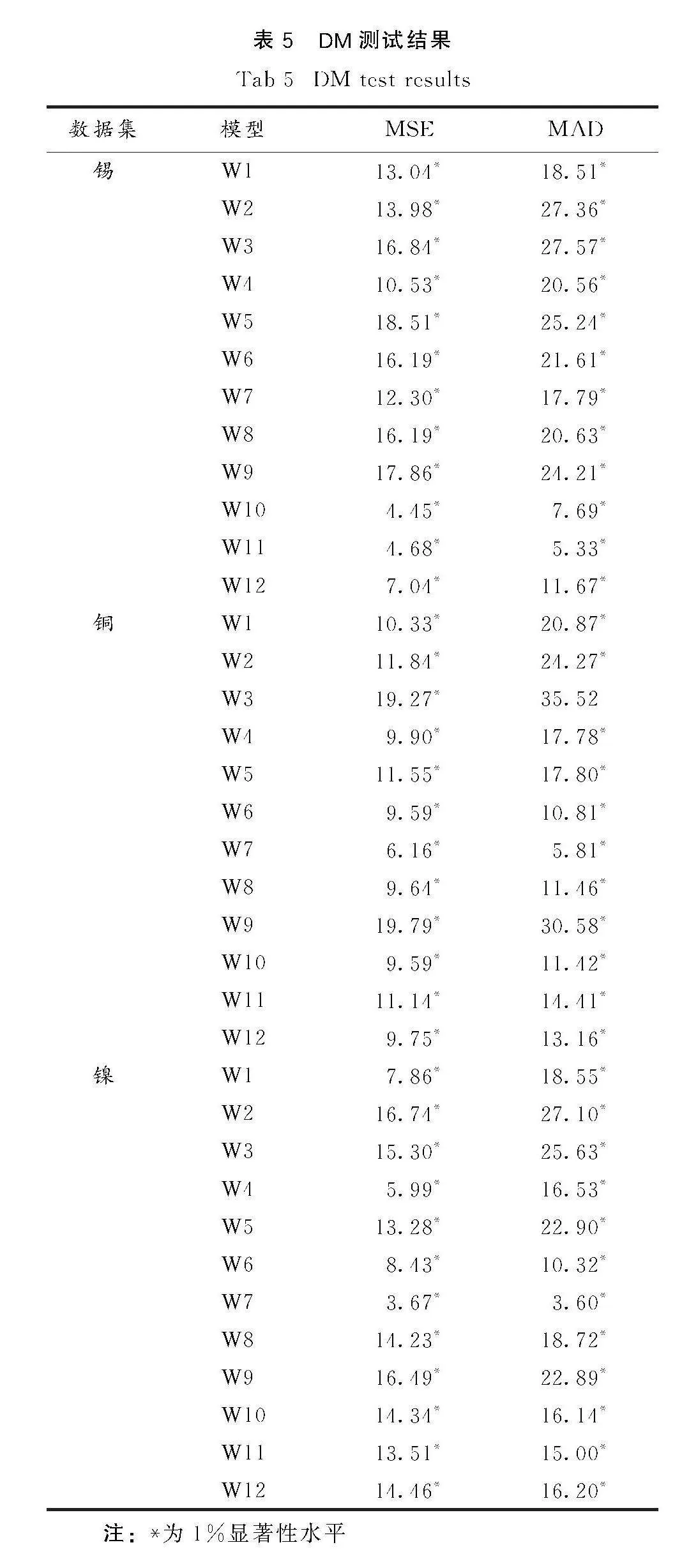
在评估两个模型的预测能力时，标准方法包括使用RMSE，MAE，MAPE和R2等评估指标来分析其性能.然而，仅比较数值可能无法全面评估模型的优缺点［30］.DM测试为此提供了更严谨的方案.DM测试的步骤参考文献［31］.DM测试结果见表 5.

DM检测的目的是比较两种模型的预测性能是否存在显著差异.DM值越大，差异越明显.从表 5中可以看出，EIRF与12个比较模型之间存在不同程度的差异.每个P值都小于0.01.DM检验进一步证实了所提出的EIRF模型比其他模型具有更好的预测能力.

3" 结论

通过对锡、铜和镍的实验分析，得出以下结论：

1）MALO算法结合Chebyshev混沌映射、差分变异扰动和黄金正弦策略，比其他优化算法更能提高VMD的自适应性.

2）提出的RFEDformer模型在FEDformer的前馈部分增加了多层感知器（MLP）.反馈部分采用了新颖的Sophia优化器和IKMSE损失函数.消融实验结果表明，该混合模型在3个数据集上提取的信息更加深入，预测效果更好.

3）实验2的结果表明，双重分解方法优于单一模型方法.二次分解进一步提取残差中的复杂信息，提高模型的预测性能.文中介绍的EIRF模型融合了数据预处理、参数优化和变压器建模等各种组件，为有色金属价格预测提供了新的途径.

参考文献：

［1］" HE Z，HUANG J.A novel non-ferrous metal price hybrid forecasting model based on data preprocessing and error correction［J］.Resour Policy，2023，86：104189.

［2］" UDDIN G S，RAHMAN M L，SHAHZAD S J H，et al.Supply and demand driven oil price changes and their non-linear impact on precious metal returns：A Markov regime switching approach［J］.Energy Econ，2018，73：108.

［3］" LASHERAS F S，DE COS JUEZ F J ，SNCHEZ A S，et al.Forecasting the COMEX copper spot price by means of neural networks and ARIMA models［J］.Resour Policy，2015，45：37.

［4］" WANG J，HU M，RODRIGUES J F.The evolution and driving forces of industrial aggregate energy intensity in China：An extended decomposition analysis［J］.Appl Energy，2018，228：2195.

［5］" ZHONG M，HE R，CHEN J，et al.Time-varying effects of international nonferrous metal price shocks on Chinas industrial economy［J］.Physica A，2019，528：121299.

［6］" KAHRAMAN E，AKAY O.Comparison of exponential smoothing methods in forecasting global prices of main metals［J］.Miner Econ，2023，36（3）：427.

［7］" DOOLEY G，LENIHAN H.An assessment of time series methods in metal price forecasting［J］.Resour Policy，2005，30（3）：208.

［8］" RUBASZEK M，KAROLAK Z，KWAS M.Mean-reversion，non-linearities and the dynamics of industrial metal prices：A forecasting perspective［J］.Resour Policy，2020，65C：101538.

［9］" ABU-DOUSH I，AHMED B，AWADALLAH M A，et al.Enhancing multilayer perceptron neural network using archive-based harris hawks optimizer to predict gold prices［J］.J King Saud Univ-com，2023，35（5）：101557.

［10］" LUO H，WANG D，CHENG J，et al.Multi-step-ahead copper price forecasting using a two-phase architecture based on an improved LSTM with novel input strategy and error correction［J］.Resour Policy，2022，79：102962.

［11］" HUANG Y T，BAI Y L，DING L，et al.Application of a hybrid model based on ICEEMDAN，Bayesian hyperparameter optimization GRU and the ARIMA in nonferrous metal price prediction［J］.Cybernetics and Systems，2023，54（1）：27.

［12］" ZHAO Y，CHEN J，SHIMADA H，et al.Non-ferrous metal price point and interval prediction based on variational mode decomposition and optimized LSTM network［J］.Mathematics，2023，11（12）：2738.

［13］" SUN J，ZHAO P，SUN S.A new secondary decomposition-reconstruction-ensemble approach for crude oil price forecasting［J］.Resour Policy，2022，77：102762.

［14］" YU C，YAN G，YU C，et al.MRIformer：A multi-resolution interactive transformer for wind speed multi-step prediction［J］.Inform Sciences，2024，661：120150.

［15］" 郭樊容，黄孝喜，王荣波，等.基于Transformer和图卷积神经网络的隐喻识别［J］.数据分析与知识发现，2022，6（04）：120.

［16］" HONG J T，BAI Y L，HUANG Y T，et al.Hybrid carbon price forecasting using a deep augmented FEDformer model and multimodel optimization piecewise error correction［J］.Expert Syst Appl，2024，247：23325.

［17］" KHAN A A，TAIBI D，PERRAULT C M，et al.Advancing quantum software engineering：A vision of hybrid full-stack iterative model［J］.arXiv-CS-Software Eng，2024.

［18］" LIU H，LI Z，HALL D，et al.Sophia：A scalable stochastic second-order optimizer for language model pre-training［J］.arXiv-MATH-Optimization and Control，2023.

［19］" BOMMIDI B S，TEEPARTHI K，KOSANA V.Hybrid wind speed forecasting using ICEEMDAN and transformer model with novel loss function［J］.Energy，2023，265：126383.

［20］" SON P V H，HIEU H T.Logistics model for precast concrete components using novel hybrid Ant Lion Optimizer（ALO） algorithm［J］.IJCM，2023，23（9）：1560.

［21］" LONG G，CHAI X，GAN Z，et al.Exploiting one-dimensional exponential Chebyshev chaotic map and matching embedding for visually meaningful image encryption［J］.Chaos Soliton Fractal，2023，176：114111.

［22］" LIN M，WANG Z，CHEN D，et al.Particle swarm-differential evolution algorithm with multiple random mutation［J］.Appl Soft Comput，2022，120（C）：108640.

［23］" LI M，LIU Z，SONG H.An improved algorithm optimization algorithm based on RungeKutta and golden sine strategy［J］.Expert Syst Appl，2024，247：123262.

［24］" HAO Y，LU J，PENG G，et al.F10.7 daily forecast using LSTM combined with VMD method［J］.Space Weather，2024，22（1）：e2023SW003552.

［25］" THURAISINGHAM R A.Revisiting ICEEMDAN and EEG rhythms［J］.Biomed Signal Proces，2021，68：102701.

［26］" ZHANG X，CHEN H，WEN Y，et al.A new rainfall prediction model based on ICEEMDAN-WSD-BiLSTM and ESN［J］.Environ Sci" Pollut R，2023，30（18）：53381.

［27］" ZIHAN LI Q Z，WEI D，YING J L，et al.FEDformer-based paddy quality assessment model affected by toxin change in different storage environments［J］.Foods，2023，12（8）：1681.

［28］" 刘海东，李星诚，张文豪.改进Adam优化器在瓦斯涌出量预测中的应用研究［J］.工矿自动化，2023，49（12）：25.

［29］" HONG J T，BAI Y L，HUANG Y T，et al.Hybrid carbon price forecasting using a deep augmented FEDformer model and multimodel optimization piecewise error correction［J］.Expert System Appl，2024，247：123325.

［30］" 孔坚锋，程飞，竺哲明，等.DM检测仪在埋地燃气管道检验中的应用［J］.中国科技信息，2022（13）：68.

［31］" CHEN H，WAN Q，WANG Y.Refined Diebold-Mariano test methods for the evaluation of wind power forecasting models［J］.Energies，2014，7（7）：4185.

（责任编辑" 孙对兄）