Breit相互作用对类铍离子电子碰撞激发过程辐射光子角分布和极化特性的影响

摘要：采用全相对论扭曲波和多组态Dirac-Fock（MCDF）方法，理论计算了高电荷态类铍离子（47≤Z≤92）在电子碰撞激发过程中，电子从基态激发到激发态1s2s22p3/2J=1的取向参数和该激发态的各磁子能级截面，进而得到了辐射跃迁1s2s22p3/2J=1→1s22s2J=0过程中辐射光子的极化度和角分布，同时讨论了Breit相互作用对磁子能级碰撞激发截面、线性极化度和角分布的影响，发现Breit相互作用对磁子能级碰撞激发截面有重要的影响，进而导致随后退激辐射谱线极化度和角分布的显著变化.

关键词：多组态Dirac-Fock方法；扭曲波方法；角分布和极化度

中图分类号：O 562.4""" 文献标志码：A""" 文章编号：1001-988Ⅹ（2025）01-0045-06

DOI：10.16783/j.cnki.nwnuz.2025.01.009

收稿日期：20240115;修改稿收到日期：20240720

基金项目：陕西省科技厅基础研究计划资助项目（2023-JC-QN-0085）;陕西省教育厅专项科研计划资助项目（22JK0423）

作者简介：王金霞（1988—），女，甘肃白银人，讲师，硕士.主要研究方向原子与分子物理.

Email：919827049@qq.com

Influence of Breit interaction on the angular distribution and

polarization characteristics of the radiated photons during

electron-impact excitation of beryllium-like ions

WANG Jin-xia1，YANG Hui-hui2，LONG Lin1

（1.Public Basic Teaching Departmengt，Chongqing College of Mobile Communication，Chongqing 404000，China;

2.Faculty of Science，Xian Aeronautical University，Xian 710077，Shaanxi，China）

Abstract：Based on the multiconfiguration Dirac-Fock（MCDF） method and the fully relativistic distorted wave method，we have calculated the electron-impact excitation cross sections from ground state to the individual magnetic sublevels and aligment parameters of the 1s2s22p3/2J=1 excited state of highy-charged beryllium-like ions（47≤Z≤92），and then obtained the angular distribution and polarization of the radiated photons of the 1s2s22p3/2J=1→1s22s2J=0 radiation transition.The influence of Breit interaction to the individual magnetic sublevels cross sections、linear polarizability and angle distribution is emphatically discussed.The results show that Breit interaction greatly changed the angular distribution and linear polarizability.

Key words：multi-configuration Dirac-Fock（MCDF） method；twisted wave method；polarizability and angle distribution

电子碰撞激发产生的激发态中各磁子能级布局遵从非统计分布规律，从而导致激发态原子退激过程中辐射出具有极化特性的光谱.而辐射出光谱的极化特性可以反映出各磁子能级的碰撞动力学过程和入射电子束的速度分布函数.因此，光谱的极化特性经过发展作为诊断等离子体中电子各向异性的工具，并且已经运用在激光等离子体［1-3］以及真空火花等离子体中［4］.

有关X射线极化特性的探究，是近几十年来人们研究的热点之一.Takács等［5］利用电子束离子阱（EBIT）实验装置研究了类氖Ba46+离子辐射谱线（2P-13/23S1/2）→2P61S0的极化特性，反映出了共振激发对辐射谱线极化特性有一定的影响；Jiang等［6］通过理论计算证实了其对极化特性的影响；Reed等［7］理论研究了相对论效应对高电荷态类氦和类氢离子电子碰撞激发过程辐射谱线线性极化度的影响，发现在非相对论情况下，谱线的线性极化度与原子序数无关，而在考虑了相对论效应后，谱线的线性极化度明显的依赖于原子序数；Ma等［8］计算了2S1/2→2P3/2电子碰撞激发的总截面和其磁子能级截面，以及部分辐射谱线的线性极化度；Bostock等［9］运用相对论RCCC方法计算高电荷态Ti21+，Ar17+，Fe25+离子碰撞激发辐射光谱的极化特性，发现通过考虑Breit相互作用可以修正理论计算和实验测量之间的差异；Wu等［10］研究了Breit相互作用对高电荷态Mo38+，Nd56+，Bi79+离子电子碰撞激发过程中辐射光子极化特性的影响.这些研究表明，Breit相互作用和相对论效应都可以极大地影响高电荷态离子辐射谱线的极化特性.

1" 理论方法

文中电子碰撞激发截面由全相对论扭曲波（DRW）程序REIE06［11］计算，靶态波函数由MCDF理论的GRASP92［12］原子结构程序包计算，连续电子波函数由RATIP［13］程序包的COWF子程序计算.

在相对论扭曲波方法中，一般选取入射电子束方向为量子化Z轴，则入射电子轨道角动量的Z分量等于0，即mli=0.能量为εi的自由电子和靶离子α（PiJiMi）发生碰撞，使靶离子从初态βiJiMi到末态βfJfMf的磁子能级碰撞激发截面为［14］

σεi（βiJiMi-βfJfMf）=

2πa20ki2∑li，l′i，ji，j′imsi，lf，jf，mf

∑J，J′，M（i）li-l′i

（（2li+1）（2l′i+1））1/2×

exp（i（δki-δk′i））Cli12mlimsi;jimi）

Cl′i12ml′imsi;j′imi）×

C（JijiMimi;JM）C（Jij′iMimi;J′M）

C（JfjfMfmf;JM）×

C（JfjfMfmf;J′M）R（γi，γf）R（γ′i，γ′f），（1）

其中，a0为玻尔半径；i和f为碰撞激发初态和末态；C为Clebsch-Gordan系数；γi=εilijiβiJiJM，γf=εflfjfβfJfJM，这里J，M分别代表碰撞体系的总角动量及其Z分量MJ之外用来标定靶离子的所有其他量子数；ki为入射电子相对论波数；δki为电子的相因子.R矩阵元为

R（γi，γf）=Ψγd∑N+1p，q，plt;qVΨγi，（2）

其中，V（电子与电子间相互作用算符）的表达式为

V=∑ilt;j1rij-（αi·αj）cos（ωrij）rij+

（αi·i）（αj·j）cos（ωrij）-1ω2rij，（3）

式中包含了库仑排斥、Breit相互作用、磁相互作用、延迟效应.αi为第i个粒子的Dirac矩阵矢量;ω为电子间交换虚光子的频率.

当入射电子与靶原子（离子）碰撞后，激发态的磁子能级一般为非统计分布，即取向的.在密度矩阵理论中［15］，激发态磁子能级的布局一般用Ak0（αfJf）取向参数或约化统计张量来描述，该参数也可以用碰撞激发截面σMf表示.例如，对于激发态1s2s22p3.2J=1，它的取向参数只有A20为非零项［16］，可表述为

A20（Jf=1）=2σ（1，±1）-σ（1，0）2σ（1，±1）+σ（1，0），（4）

其中σ（1，0）和σ（1，±1）为从基态到激发态磁子能级Mf=0和Mf=±1的碰撞激发截面.

电子碰撞激发所形成的激发态的磁子能级的取向性，将导致辐射跃迁放出的光子有线性极化特性和各向异性角分布.而对于电偶极辐射跃迁，碰撞激发过程中辐射光子的角分布为［16，17］

WE1（θ）∝1+β2P2（cosθ），（5）

各向异性参数可表示为

β2≡β2（αfJf，αkJk）=

f2（αfJf，αkJk）A20（αfJf），（6）

β2，f2（αjJf，αkJk）为辐射跃迁过程的结构函数；P2（cosθ）为二阶勒让德多项式；θ为入射电子与之间发出光子的夹角，通常依赖于具体的电子结构和辐射跃迁过程.在实验上通过测量辐射跃迁谱线强度来得到线性极化度，其定义式为［18］

P=I‖-I⊥I‖+I⊥，（7）

其中，I⊥和I‖分别为辐射光子电矢量垂直于电子束方向和平行电矢量的光强.

对于J=1到J=0谱线的线性极化度［18］表达式为

p=σ0-σ1σ0+σ1，（8）

其中，σ（1，0）和σ（1，±1）为从基态到激发态磁子能级Mf=0和Mf=±1的碰撞激发截面.

2" 结果与讨论

为了说明本文中计算体系波函数和能级的可靠性，以及对各种效应考虑的合理性，同时为了确保

分波的收敛性，取入射（或散射）电子的最大相对论量子数K=50，表1给出了当入射电子能量为20 keV时，高电荷态Mo38+从基态碰撞激发到1s2s22p3/2J=1的磁子能级碰撞激发截面和取向参数A20.并且和文献［19］做了比较，由表1可以看到，文中计算的结果与文献中结果符合的非常好.表2列出了Mo38+，W70+，U88+离子电子碰撞激发过程的激发能，其中C表示不包括Breit相互作用时的计算结果，C+B表示包括Breit相互作用的计算结果，并且与Shi等［20］计算的结果做了比较，可以看到，不管包括Breit相互作用还是不包括Breit相互作用，文中的计算结果与文献中的都符合的非常好.

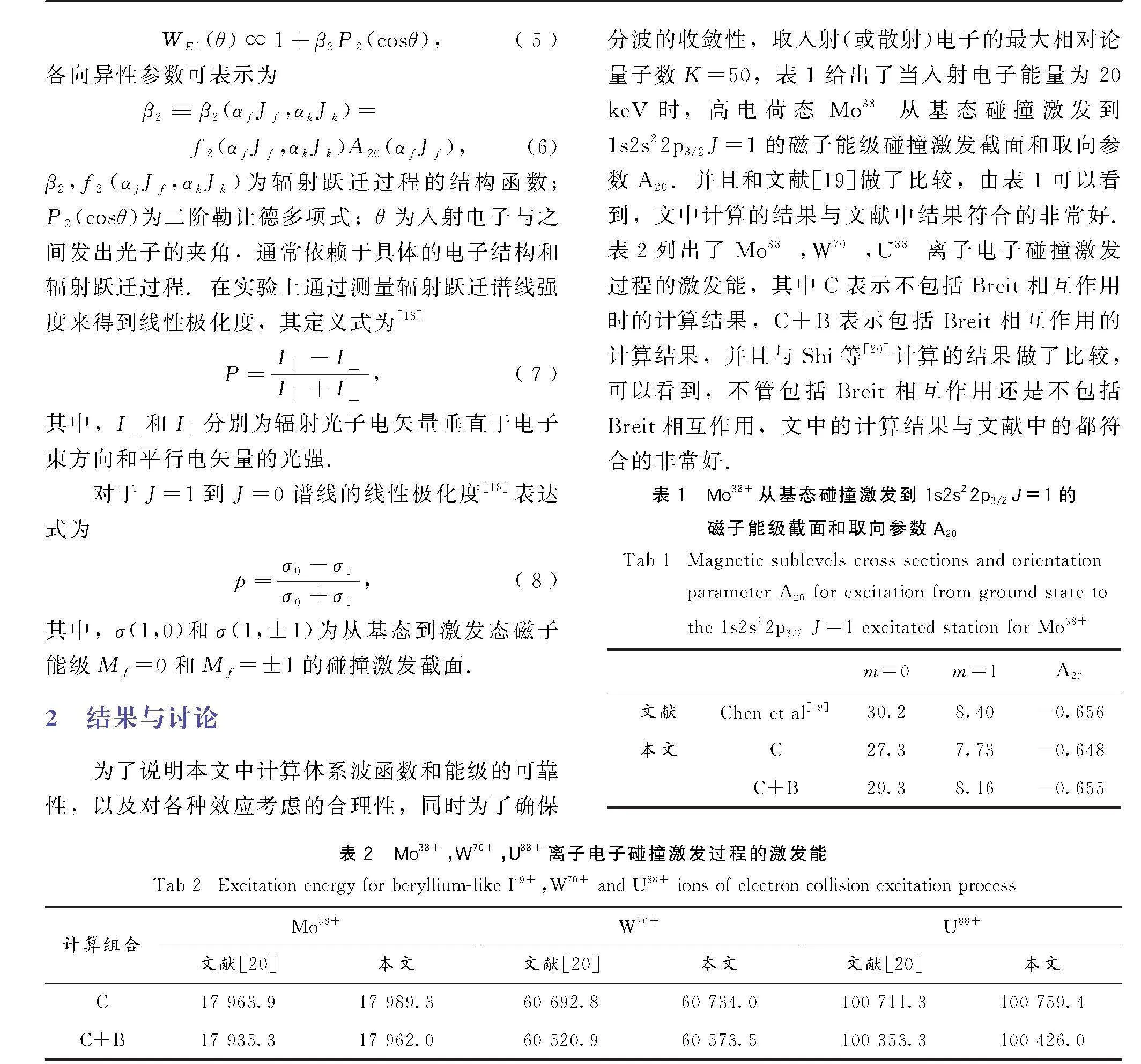
图1给出了类铍I49+，W70+，U88+离子电子碰撞激发过程总截面随入射电子能量变化的曲线，其中C表示不包括Breit相互作用的计算结果，C+B表示包括Breit相互作用的计算结果.首先，对于I49+离子，由图1可以看出，不包括Breit相互作用时，激发过程中总截面随入射电子能量的增大先增大，当电子能量增大到两倍阈值时总截面达到最大值，然后又随入射电子能量的增大而减小，当包括了Breit相互作用后，激发过程中总截面随入射电子能量的变化关系和不包括Breit相互作用的相似，并且包括了Breit相互作用后，使得总截面减小；对于W70+，U88+离子电子碰撞激发过程总截面，随入射电子能量的变化规律和I49+离子的变化规律相似，并且随着核电荷数的增加Breit相互作用对总截面的影响越来越大.

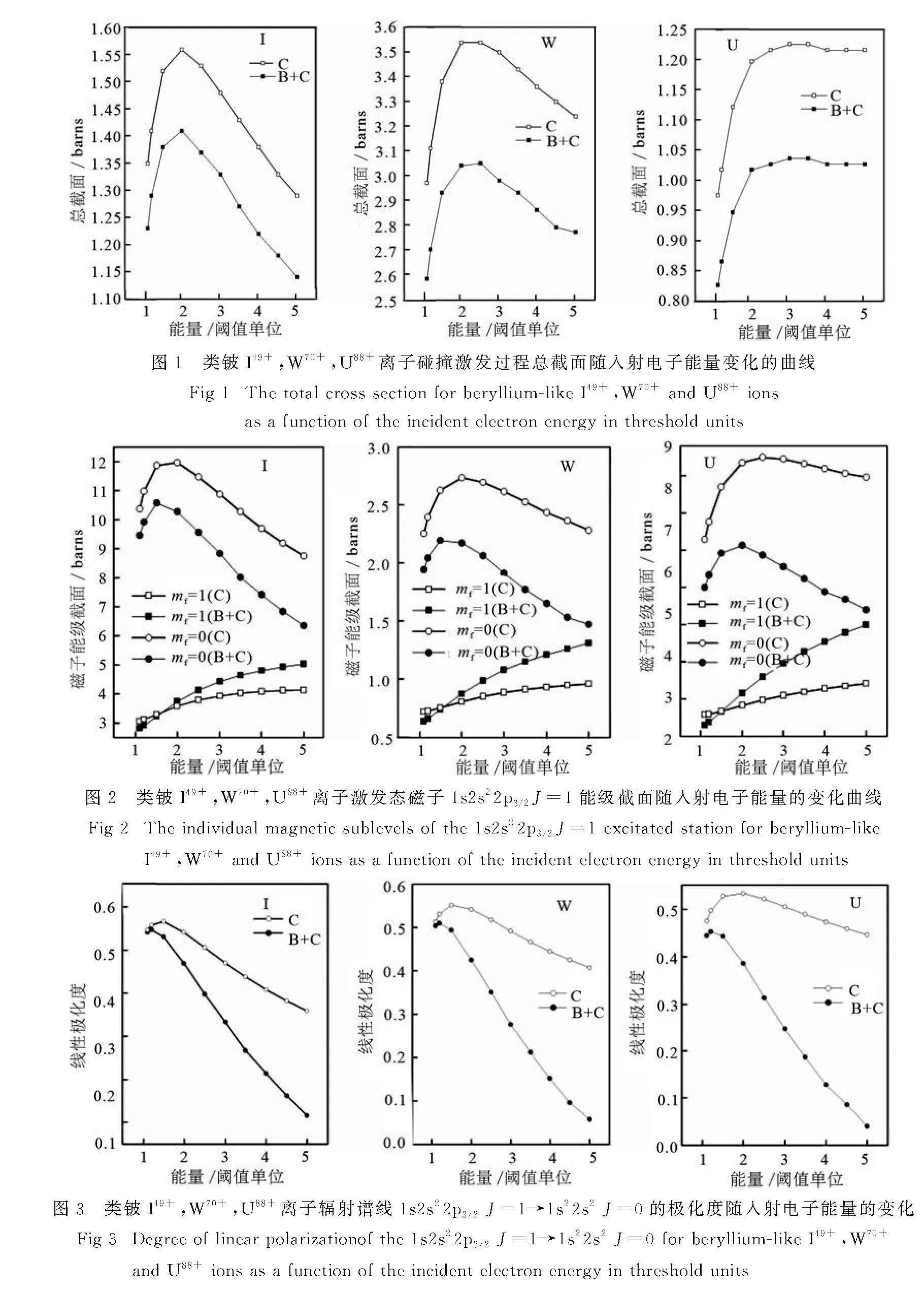
图2为类铍I49+，W70+，U88+离子电子碰撞激发到激发态的1s2s22p3/2J=1和mf=1的磁子能级截面，其中C+B表示考虑Breit相互作用，C表示不考虑Breit相互作用.从图2可以看到，对于给定的入射电子能量，不管包括还是不包括Breit相互作用时，磁子能级mf=0的截面要比磁子能级mf的截面大.而磁子能级mf=0的截面先随入射电子能量的增大而增大，当能量增大到2倍阈值时截面达到最大值，然后随入射电子能量的增大而减小；而磁子能级mf=1的截面在5倍阈值的能量范围内都随入射电子能量的增大而增大.同时能够看出，Breit相互作用使得磁子能级mf=0的截面减小，mf=1的截面增大.且随核电荷数的增加，Breit相互作用对磁子能级截面的影响越来越大.

图3给出了类铍I49+，W70+，U88+离子电子碰撞激发过程中辐射谱线的极化度随入射电子能量的变化，其中C表示不包括Breit相互作用的计算结果，C+B表示包括Breit相互作用之后的计算结果.对于I49+离子，可以看出，不包括Breit相互作用时，碰撞激发过程谱线极化度随入射电子能量的增大缓慢的减小，而当考虑了Breit相互作用后，Breit相互作用使得谱线的极化度随入射电子能量的增大而迅速的减小.由极化度公式（8）和图1中磁子能级截面能够得到同样的变化趋势.对于W70+，U88+离子，极化度随入射电子能量的变化与

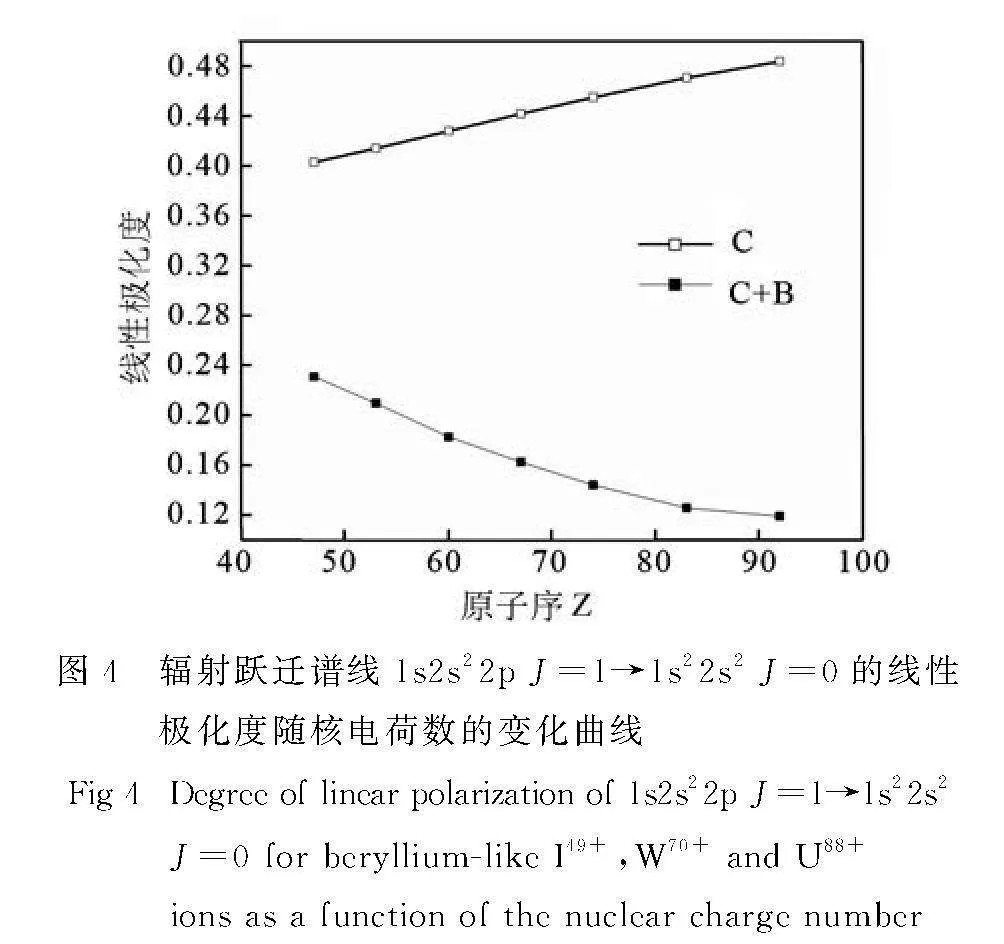
极化度随核电荷数的变化曲线

Fig 4Degree of linear polarization of 1s2s22p J=1→1s22s2

J=0 for beryllium-like I49+，W70+ and U88+

ions as a function of the nuclear charge number

I49+有相似的规律，由图可以看出随着核电荷数的增大，Breit相互作用对极化度的影响越来越大.

图4给出了当入射电子能量为4倍阈值时，包括Breit相互作用和不包括Breit相互作用时类铍离子（47lt;Zlt;92）电子碰撞激发辐射谱线的极化度随核电荷数的变化曲线.在不包括Breit相互作用时，随核电荷数的增大谱线的线性极化度缓慢增加，而在考虑了Breit相互作用后，线性极化度随核电荷数的增大而急剧减小，且随核电荷数的增大，Breit相互作用的影响越来越大.

图5给出了类铍I49+，W70+，U88+离子在电子碰撞激发过程中辐射光子的角分布.当不考虑Breit相互作用只考虑库仑相互作用时，I49+，W70+，U88+离子辐射出光子的方向倾向于入射电子束的垂直方向.当考虑了Breit相互作用后，I49+发出沿垂直于入射电子束方向的光子有所减弱，沿平行于入射电子方向的光子有所增强，W70+发出沿垂直于入射电子束方向的光子明显减弱，沿平行于入射电子方向的光子明显增强，而U88+发出光子的方向明显倾向于沿平行于入射电子的方向.因此随着核电荷数的增加，Breit相互作用对光子角分布的影响也越来越大.

3" 结束语

文中详细计算了高电荷态类铍离子（47≤Z≤92）内壳层电子碰撞到激发态1s2s22p3/2 J=1的磁子能级截面，进而得到了退激发辐射光子的角分布和极化度.重点讨论了Breit相互作用对其角分布和线性极化度的影响，结果表明，Breit相互作用作为库仑排斥的修正，使得电子碰撞激发到激发态的总截面减小，进而改变了辐射谱线的角分布和极化度.在给定入射电子能量的情况下，Breit相互作用使得谱线的线性极化度减小，并且随核电荷数的增加，Breit相互作用作对谱线的极化特性的影响越来越大.

参考文献：

［1］" KIEFFER J C，MATTE J P，PPIN H，et al.Electron distribution anisotropy in laser-produced plasmas from x-ray line polarization measurements［J］.Phys Rev Lett，1992，68（4）：480.

［2］"" KIEFFER J C，MATTE J P，CHAKER M，et al.X-ray-line polarization spectroscopy in laser-produced plasmas［J］.Phys Rev E，1994，48（6）：4648.

［3］" HAKEL P，MANCINI R C，GAUTHIER J C，et al.X-ray line polarization of He-like Si satellite spectra in plasmas driven by high-intensity ultrashort pulsed lasers［J］.Phys Rev E，2004，69（5）：056405.

［4］" BEUER R，BACHMANN C，BURHENN R.Investigation of the polarisation of nonthermal bremsstrahlung from a vacuum spark plasma［J］.J Phys D，1981，14（4）：643.

［5］" TAKCS E，MEYER E S，GILLASPY J D，et al.Polarization measurements on a magnetic quadrupole line in Ne-like barium［J］.Phys Rev A，1996，54（2）：1342.

［6］" DONG C Z，WANG J G.Resonance electron-impact excitation and polarization of the magnetic quadrupole line of neonlike Ba46+ ions［J］.Phys Rev A，2008，78（2）：022709.

［7］" REED K J，CHEN M H，Relativistic effects on the polarization of line radiation emitted from He-like and H-like ions following electron-impact excitation［J］.Phys Rev A，1993，48（5）：3644.

［8］" MA X Y，DONG C D，WU Z W，et al.Theoretical study on electron-impact excitation processes and the relevant polarization of radiation of 2s1/2-2p3/2 in W65+ through W71+［J］.Acta Phys Sin，2012，61（21）：213401.

［9］" BOSTOCK C J，FURSA D V，BEAY I，Relativistic convergent close-coupling method：Calculation of electron scattering from hydrogenlike ions［J］.Phys Rev A，2009，80（5）：2554.

［10］" WU Z W，DONG C Z，JIANG J，et al.Influence of Breit interaction on the polarization of radiation following inner-shell electron-impact excitation of highly charged berylliumlike ions［J］.Phys Rev A， 2011，84（3）：19781.

［11］" JIANG J，DONG Z C，XIE L Y，et al.Relativistic distorted-wave calculations of electron impact excition cross section of Be-like C2+ ions［J］.Chin Phys Lett，2007，24：691.

［12］" PRAPIA F A，FISCHER C F，GRANT I P，et al.GRASP92：A package for larger-scale relativistic atomic structure calculations［J］.Comput Phys Commun，1996，94：249.

［13］" FRIZSCHE S，AKSELA H，DONG C Z，et al.Theoretical Auger and photoionization studies for open-shell atoms and ions［J］.Nucl Instrum Methods Phys Res B，2003，205（1）：93.

［14］" ZHANG H L，SAMPSON D H，CLARK R E H，et al.Relativistic cross section for excition of highly charged ions to specific magnetic sublevels by an electron beams［J］.Phys Rev A，1990，41（1）：198.

［15］" WU Z W，JIANG J，DONG C Z，Influence of Breit interaction on the polarization of radiation following inner-shell electron-impact excitation of highly charged berylliumlike ions［J］.Phys Rev A，2011，84（3）：19781.

［16］" BALASHOV V V，GRUM-GRZHIMAILO A N，KABACHINK N M.Polarization and Correlation Phenomena in Atomic Collisions［M］.New York：Kluwer Academic/Plrnum，2000.

［17］" BEREZHKO E，KABACHNIK N M.Theoretical study of inner-shell alignment of atoms in electron impact ionisation：Angular distribution and polarisation of X-rays and Auger electrons［J］.J Phys B，1977，10（12）：2467.

［18］" PERCIVAL I C，SEATON M J.The polarization of atomic line radiation excited by electron impact［J］.Roy Soc Lond Philosophical Transactions Series A，1958，251（990）：113.

［19］" CHEN M H，SCOFILD J H.Relativistic effects on angular distribution and polarization of dielectronic satellite lines of hydrogenlike ions［J］.Phys Rev A，1995，52（3）：2057.

［20］" SHI Y L，DONG C Z，MU X Y，et al.Theoretical atudy on the electron collision processes of highly charged ions and related angular properties［J］.Chin Phys Lett，2013，30（6）：063401.

（责任编辑" 孙对兄）