近年高考新课标Ⅰ卷三角函数试题分析及教学启示

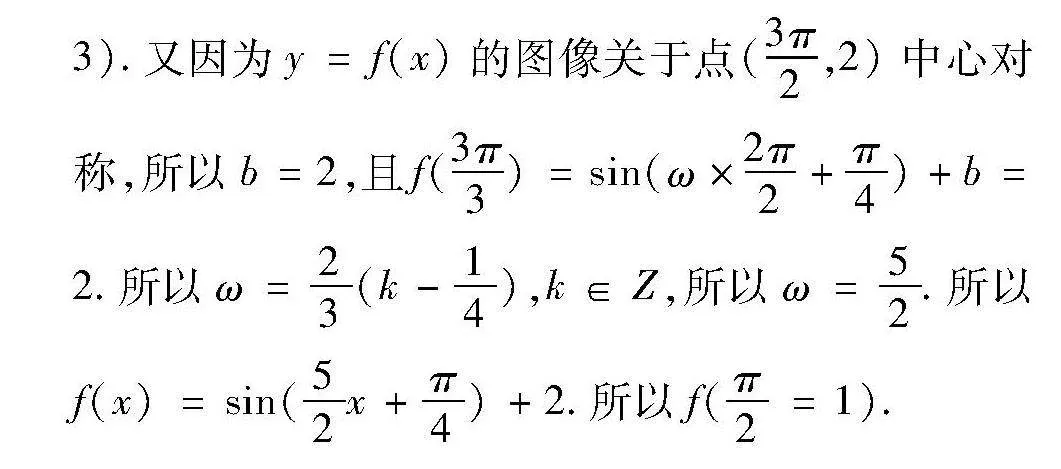
1.研究缘起

2021-2024年高考新课标Ⅰ卷三角函数试题引起了广泛关注，这不仅是因为它们在高考数学卷中的稳定出现，更重要的是这些试题在命题思路、知识点考察深度及广度等方面都展现出显著的特点.三角函数作为高中数学的重要内容，其试题设计在难度、考察重点及与其他知识点的交叉方面不断变化，反映了教学大纲和课程标准的调整.对这些试题的系统分析可以帮助教师更好地理解高考命题趋势，从而调整教学策略，提升学生应对高考的能力.

2.考查占比与趋势

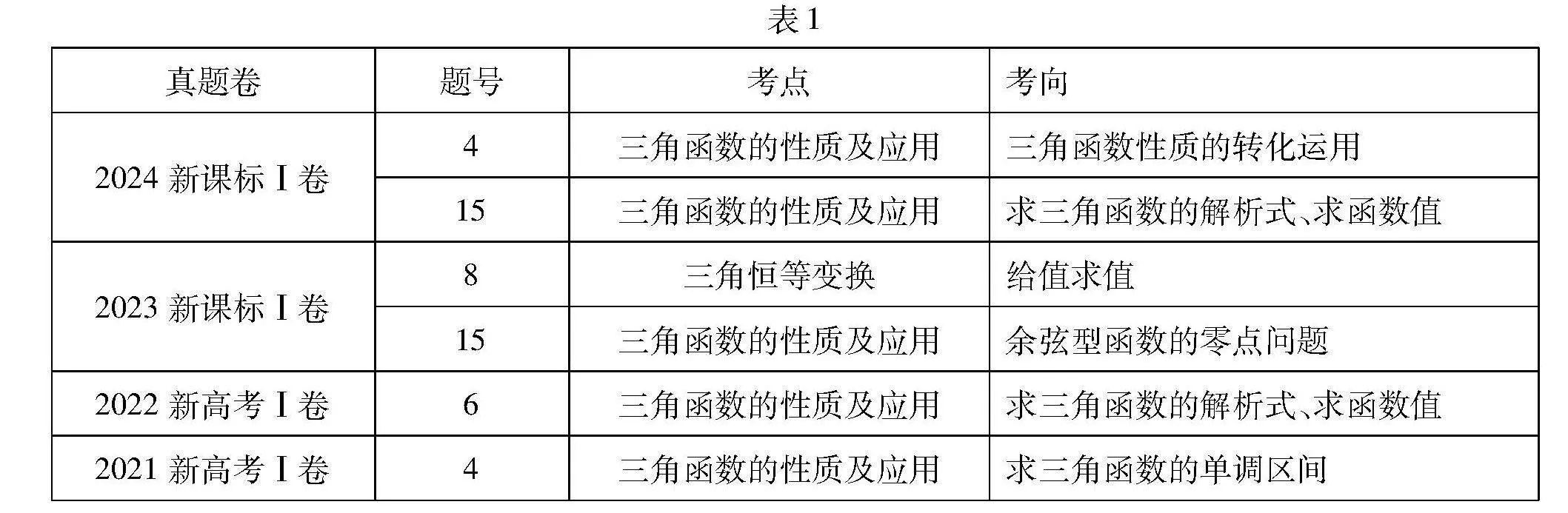
分析三角函数试题首先要明确考查占比与趋势，因为这能帮助我们准确把握该知识点在整个试卷中的地位和重要性.了解三角函数在高考试卷中的考查频率和比重，有助于制定更有效的教学和复习策略，推动学生更好的掌握重点以及突破高频考点.2021-2024年高考新课标Ⅰ卷三角函数试题的统计见表1.

表1

真题卷题号考点考向

2024新课标Ⅰ卷

4三角函数的性质及应用三角函数性质的转化运用

15三角函数的性质及应用求三角函数的解析式、求函数值

2023新课标Ⅰ卷

8三角恒等变换给值求值

15三角函数的性质及应用余弦型函数的零点问题

2022新高考Ⅰ卷6三角函数的性质及应用求三角函数的解析式、求函数值

2021新高考Ⅰ卷4三角函数的性质及应用求三角函数的单调区间

3.考查重点

在2021-2024年高考新课标Ⅰ卷中，三角函数的性质及其应用是考查的重点内容.每年的试题中都会涉及到三角函数的基本性质，包括周期性、奇偶性、对称性等.这类题目要求学生不仅能够准确记忆和理解三角函数的基本性质，还能将其应用到具体问题的解答中，如求解三角方程以及不等式等.结合题型来看，相较于2021年和2022年试题，2023新课标Ⅰ卷和2024新课标Ⅰ卷在选择题和问答题中均考查了三角函数，这反映了三角函数知识考查的稳定性和重要性

4.考查特点例析

例1" （2023新课标Ⅰ卷第15题）已知函数f（x）=cosωx-1（wgt;0）在区间［0，2π］有且仅有3个零点，则ω的取值范围是""" ．

析解" 本题考查了余弦型函数的零点问题，令f（x）=0，得有3个根，从而结合余弦函数的图像性质即可得解．令f（x）=cosωx-1=0，得cosωx=1，又x∈［0，2π］，则ωx∈［0，2ωπ］，所以4π≤2ωπ＜6π，得2≤ω＜3故答案为［0，3）

例2" （2024新课标Ⅰ卷第15题）记△ABC内角A、B、C的对边分别为a，b，c，已知sinC=2cosB，a2+b2－c2=2ab.（1）求B；（2）若的面积为3+3，求c．

析解" （1）由余弦定理、平方关系依次求出cosC，sinC，最后结合已知sinC=2cosB得cosB的值即可；（2）首先求出A，B，C，然后由正弦定理可将a，b均用含有c的式子表示，结合三角形面积公式即可列方程求解.具体解答过程为：（1）由余弦定理有a2+b2－c2=2abcosC，对比已知a2+b2－c2=2ab，可得cosC=a2+b2－c22ab=2ab2ab=22因为C∈0，π，所以sinCgt;0，从而sinC=1－cos2C=1－222=22，又因为sinC=2cosB，即cosB=12，注意到B∈0，π，所以B=π3.

（2）由（1）可得B=π3，cosC=22，C∈0，π，从而C=π4，A=π－π3－π4=5π12，而sinA=sin5π12=sinπ4+π6=22×32+22×12=6+24，由正弦定理有asin5π12=bsinπ3=csinπ4，从而a=6+24·2c=3+12c，b=32·2c=62c，由三角形面积公式可知，的面积可表示为，由已知的面积为3+3，可得3+38c2=3+3，所以c=22.

评注" 在2021-2024年的高考新课标Ⅰ卷中，三角函数的性质是一个重要的考查内容.试题要求学生深入理解三角函数的周期性、奇偶性、对称性等基本性质，并能够应用这些性质解决实际问题.例如，利用周期性简化复杂的计算，或运用对称性判断函数图像的特征.这种考查方式不仅检验学生对基本概念的掌握情况，还考查他们在实际问题中灵活运用这些性质的能力.②函数变换与解析技巧的运用：三角函数的函数变换在高考试题中占据重要位置，选取的例题考查了三角函数性质的转化运用，可以看到这类题目要求学生能够熟练运用平移、伸缩、反转等函数变换，分析并利用这些变换解决复杂的三角函数问题.此外，还涉及到图像的绘制与分析，要求学生能够准确理解变换对图像特征的影响.

例3" （2023新课标Ⅰ卷第8题）已知sinα－β=13，cosαsinβ=16，则cos2α+2β=（"" ）．

A. 79" B. 19" C.－19" D.－79

析解" 三角函数求值的类型及方法：“给角求值”：一般所给出的角都是非特殊角，从表面来看较难，但非特殊角与特殊角总有一定关系．解题时，要利用观察得到的关系，结合三角函数公式转化为特殊角的三角函数；“给值求值”：给出某些角的三角函数值，求另外一些角的三角函数值，解题关键在于“变角”，使其角相同或具有某种关系；“给值求角”：实质上也转化为“给值求值”，关键也是变角，把所求角用含已知角的式子表示，由所得的函数值结合该函数的单调区间求得角，有时要压缩角的取值范围．

因为sin（α－β）=sinαcosβ－cosαsinβ=13，而cosαsinβ=16，因此sinαcosβ=12，则sin（α+β）=sinαcosβ+cosαsinβ=23，所以cos（2α+2β）=cos2（α+β）=1－2sin2（α+β）=1－2×（23）2=19.故选B.

例4 "（2022新课标Ⅰ卷第6题）记函数f（x）=sin（ωx+π4+b）（ω＞0）的最小正周期为T.若2π3＜T＜π，且y=f（x）的图像关于点（3π2，2）中心对称，则f（π2）=（" ）.

A.1""" B.32""" C.52""" D.3

析解" 根据周期范围，确定ω范围，再根据对称中心确定ω=23（k-14），k∈Z，二者结合可得结果．由题可知T=2πω∈（2π3，π），所以ω∈（2，3）．又因为y=f（x）的图像关于点（3π2，2）中心对称，所以b=2，且f（3π3）=sin（ω×2π2+π4）+b=2．所以ω=23（k-14），k∈Z，所以ω=52.所以f（x）=sin（52x+π4）+2.所以f（π2=1）．

评注" 高考新课标Ⅰ卷的三角函数试题还注重知识融合运算能力的应用拓展.这包括将三角函数知识与其他数学领域（如向量、解析几何等）进行融合应用，解决复杂的实际问题.试题通常要求学生能够跨学科地运用数学知识，创造性地解决实际问题，体现数学的应用性和创新性.

5.教学启示

5.1.立足教材，夯实知识与能力之基

针对高考新课标Ⅰ卷中的三角函数试题，教师可以从以下两个方面着手，以夯实学生的知识和能力基础：①深入理解教材要点和考试重点：理解教材中关于三角函数的基本概念、性质、公式及其推导，例如正弦、余弦、正切函数的定义、周期性、奇偶性等特性.确保学生对这些基础知识的掌握是扎实的；分析历年高考试卷，特别是近几年的新课标Ⅰ卷，了解三角函数试题的出题规律和重点.重点关注各类题型如基本计算、综合应用、证明题等，确保学生能够熟练应对各种形式的考题.②强化学生的知识和能力训练：利用系统化的教学方法，逐步深入讲解三角函数的各个方面.通过清晰的知识结构和示例问题，帮助学生建立扎实的基础；设计多样化的练习和应用题，旨在培养学生的分析、解决问题和推理能力.这些练习不仅要涵盖基础知识的应用，还要考验学生在复杂情境下的应变能力.

5.2.注重数学思想方法和多元知识的融合

教师要强调三角函数在几何图形中的应用，例如正弦和余弦函数与直角三角形的关系，以及正弦定理、余弦定理在三角形和多边形内外角的应用等.通过几何图形的展示和分析，帮助学生直观理解三角函数的定义和性质.此外，使用图形化方法，如函数图像、极坐标图等，让学生探索三角函数的周期性、对称性和变换规律.通过对图形的分析，引导学生发现函数的基本特征，并理解这些特征如何与数学概念相互关联.

参考文献

［1］罗瑶，张映辉，王素素.近五年高考全国卷三角试题分析与备考建议［J］.中学数学，2023，（07）：43-46.