一题多变：典型教材习题的探究与拓展

一题多变的变式教学和训练有助于学生掌握知识和提升能力.以“一核、四层、四翼”高考评价体系为指引，一题多变教学策略主要体现在“四层、四翼”的教学评价体系中.在这种评价体系中，“一题多变”的教学策略可以作为一种教学方法，有助于帮助学生理解问题、掌握知识、提高思维能力和创新能力.同时，“一题多变”也符合“四翼”中关于教学评价的思路，即多元化评价，包括过程性评价、表现性评价等多种评价方式.通过一题多变的变式教学和训练，可以帮助学生从不同角度理解问题，从而更好地掌握知识，提高发散思维能力和创新能力.

一题多变的变式教学和训练较好地适用于解析几何中定点问题、角度或斜率问题、面积或面积最值问题的思考.在高中数学教学中，学生面对的主要问题之一就是如何在数学中提升自己的思维能力与问题解决能力.圆锥曲线部分可以较好地考查数形结合、函数与方程、转化与划归等数学思想，体现对直观想象、数学运算、逻辑推理、数学抽象等关键学科核心素养的考核，是高考的重要考点，在高考中所占比重非常大.笔者通过搜索和查找2014年到2023年高考全国新课标I卷、新课标II卷、新课标Ⅲ卷、甲卷文理科和乙卷文理科解析几何解答题的考题和考点，发现解析几何中定点问题、角度或斜率问题、面积或面积最值问题是高频考点，三类重要考点几乎覆盖所有年份，分别统计如下：

（1）.定点问题：2023年新课标Ⅱ卷理科21、2023年全国乙卷理科20文科21、2022年全国乙卷理科20文科21、2020年新课标Ⅰ卷理科20文科21、2019年新课标Ⅲ卷理科21、2017年新课标Ⅰ卷理科20.

（2）.角度或斜率问题：2021年新课标Ⅰ卷理科21、2018年新课标Ⅰ卷理科19文科20、2015新课标Ⅰ卷理科20.

（3）.面积或面积最值问题： 2023年全国甲卷理科20文科21、2022年新课标Ⅰ卷理科21、2021年全国乙卷理科21、2020新课标Ⅱ卷理科21、2020年新课标Ⅲ卷理科20文科21、2019年新课标Ⅱ卷理科21、2019年新课标Ⅲ卷理科21、2016年新课标Ⅰ卷理科20、2014年新课标Ⅰ卷理科20.

一题多变的变式教学和训练蕴含着巨大的学生数学核心素养培养价值.美国著名数学教育家波利亚指出：“一个专心地认真备课的教师能拿出一个有意义的但不复杂的问题去帮助学生发掘问题的各个方面，使得通过这道题就好像通过一道门户，把学生引入一个完整的领域”.新教材中的一些典型例题或课后习题，都是我们可钻研的资源，这些题目典型、知识丰富、综合性强、灵活度高，如果有针对性地加以运用、有理论性地加以引导、有目标性地加以探索、有思维性地加以扩展，则能够全面提升和培养学生的直观想象、数学运算、数学建模、逻辑推理以及数学抽象等数学学科核心素养.

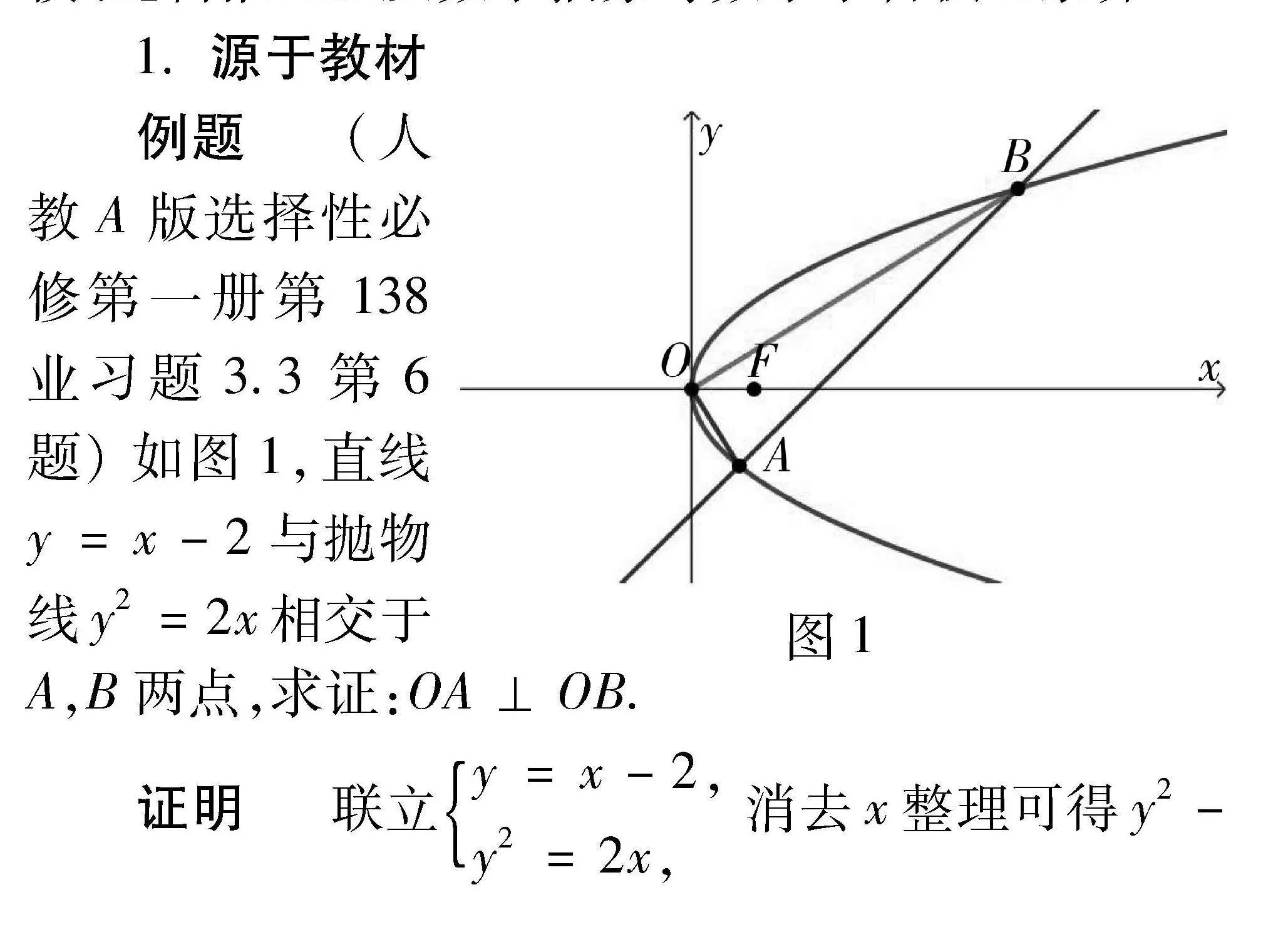
1. 源于教材

图1

例题" "（人教A版选择性必修第一册第138业习题3.3第6题）如图1，直线y=x－2与抛物线y2=2x相交于A，B两点，求证：OA⊥OB.

证明" "联立y=x－2，

y2=2x， 消去x整理可得y2-2y-4=0.

设A（x1，y1），B（x2，y2），则y1y2=－4.所以kOA ·kOB" = y1x1·y2x2 = y1y2y122·y222 = 4y1y2 =- 1，故OA⊥OB.

以上问题的实质就是抛物线的弦对顶点张直角，可利用抛物线与直线联立，利用韦达定理证出结论.下面，笔者以该题为载体进行变式探究与拓展，研究圆锥曲线点线面位置关系常考知识点—定点问题、角度或斜率问题、面积或面积最值问题的解题方法和策略，结合逻辑推理和数学运算，得到相关问题的一些优美结论.

2. 变式探究与拓展

2.1 定点问题

在解析几何中，有些含有参数的直线或曲线的方程，不论参数如何变化，其都过某定点，这类问题称为定点问题.证明直线（曲线）过定点的基本思想是确定方程，即使用一个参数表示直线（曲线）方程，根据方程成立与参数无关得出关于x，y的方程组，以方程组的解为坐标的点就是直线（曲线）所过的定点.一般来说，“特殊位置法”（先猜想后证明）和“去参数法”（让参数失效）是处理这类问题的常用方法.

变式1" 直线AB与抛物线y2=2x相交于A，B两点，若OA⊥OB，求证：直线AB恒过定点.

本题通过交换习题中的条件和结论，考查直线与抛物线相交，两交点与顶点张直角的条件下，直线过定点问题，全面考查解析几何中解决定点的通性通法，对考生的逻辑思维能力、分析问题和解决问题的能力有一定要求，具有较好的区分度.

解法1" （代数法） 设A（x1，y1），B（x2，y2），直线AB的方程为x=my+t.

联立x=my+t，y2=2x， 消去x整理可得y2-2my-2t=0.由韦达定理可得y1y2=-2t，所以kOA ·kOB" = y1x1·y2x2 = y1y2y122·y222 = 4y1y2 =- 2t，而由OA⊥OB，可得kOA·kOB=-2t=-1，t=2.直线x=my+2恒过定点（2，0）.

解法2" （齐次化） 设A（x1，y1），B（x2，y2），直线AB的方程为mx+ny=1.

联立mx+ny=1，

y2=2x， mx+ny=y22x，得（yx）2-2nyx-2m=0，因为kOA=y1x1，kOB=y2x2是方程的两根.

由韦达定理可得kOA·kOB=-2m=-1，所以m=12.

直线（12x-1）+yn=0恒过定点（2，0）.

注" 解法1和解法2都是采用代数法：设出直线方程，联立直线与抛物线，结合韦达定理寻找直线中两个参数之间的联系，代入直线方程后分离参数，解关于x，y的方程组即得定点.

结论1" 直线AB与抛物线y2=2px相交于A，B两点，若OA⊥OB，则直线AB恒过定点（2p，0）.

证明" "设A（x1，y1），B（x2，y2），直线AB的方程为x=my+t.

联立x=my+t，

y2=2px， 消去x整理可得y2-2pmy-2pt=0.由韦达定理可得y1y2=-2pt，所以kOA ·kOB" = y1x1·y2x2 = y1y2y122p·y222p = 4p2y1y2 =" - 2pt，而由OA⊥OB，可得kOA·kOB=-2pt=-1，t=2p.从而直线AB恒过定点（2p，0）.

推广" 直线AB与抛物线y2=2px相交于A，B两点，若kOA·kOB=λ（λ为非零常数），则直线AB恒过定点（-2pλ，0）.

推广的证明可参照结论1的证明加以分析与处理，或可采用齐次化加以证明，这里不多赘述.其中，结论1是推广的特例，是当常数λ=-1时的结果.类似的高考题还有2017年全国Ⅰ卷理科第20题，作为练习1供读者使用.

练习1 （2017年高考新课标Ⅰ卷20）已知椭圆C：x24+y2=1，设不经过点P2（0，2）的直线l与椭圆C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明： l过定点．

2.2" 角度或斜率问题

圆锥曲线与角度或斜率相关的问题一直是高考命题的热点.此类问题融合了三角函数、平面向量、不等式等知识，考查学生逻辑思维能力、运算求解能力和转化与划归思想解决问题的能力.通常，把角度问题转化为斜率、向量、三角函数等.通过研究斜率的关系、运用向量的坐标运算、求解三角函数值等，或直接通过到角公式，解决与角度相关的问题.

变式2" 设抛物线C：y2=2x，点A（2，0），B（－2，0），过点A的直线l与C交于M，N两点.证明：∠ABM=∠ABN.

本题考查了直线与抛物线相交的基本概念和方法，突出考查了解析几何的基本思想，全面考查了考生的逻辑推理、直观想象、数形结合、数学运算等数学学科核心素养.

解法1" "依题意知直线斜率不为0，设直线方程为l：x=my+2，联立x=my+2，

y2=2x， 得y2-2my-4=0.

设点M（x1，y1），N（x2，y2），则y1+y2=2m，y1y2=-4，kMB+kNB=y1x1+2+y2x2+2=2my1y2+4（y1+y2）（x1+2）（x2+2）=－8m+8m（x1+2）（x2+2）=0，所以kMB=－kNB，故得∠ABM=∠ABN.

图2

解法2" "当l与x垂直时，AB为∠MBN的角平分线，所以∠ABM=∠ABN；

当l与x轴不垂直时候，设l的方程为y=k（x-2），M（x1，y1），N（x2，y2），

过M，N分别作x轴的垂线，垂足依次为C，D，如图2所示.

∠ABM=∠ABNtan∠ABM=tan∠ABNy1x1+2=y2x2+2，则y1x1+2=-y2x2+2y1x1+2+y2x2+2=0，以下同解法1.

解法3" "当l与x垂直时，AB为∠MBN的角平分线，所以∠ABM=∠ABN；

当l与x轴不垂直时候，设l的方程为y=k（x-2），M（x1，y1），N（x2，y2），

图3

设点N（x2，y2）关于x轴的对称点为C（x2，-y2），如图3所示.于是，

∠ABM=∠ABNB，C，M三点共线kBC=kBM，即y1x1+2=－y2x2+2y1x1+2+y2x2+2=0，以下同解法1.

注" 变式2即为2018年全国Ⅰ卷文科数学第20题.解法1采用代数法，将角度问题转化为证明倾斜角互补，即它们的斜率之和为0，联立抛物线和直线，利用韦达定理可计算求得结论；解法2转化为三角函数，直接证正切值相等；解法3通过对称点转化证明三点共线.解法2和解法3都属于几何法，但与解法1一样，都要利用直线与抛物线联立，设而不求，利用韦达定理证明相关的结论，这是处理直线与圆锥曲线的通法.

结论2" 已知抛物线C：y2=2px（pgt;0），M（m，0），N（n，0）是x轴上不同的两点（异于抛物线的顶点）.过点N作直线l与抛物线C交于A，B两点，则直线MA和直线MB与x轴所成的角相等的充要条件是m+n=0.

证明" "由条件知l的斜率不为零，设l的方程为x=ty+n，A（x1，y1），B（x2，y2），

由x=ty+n，

y2=2px， 得y2－2pty－2pn=0，所以y1+y2=2pt，y1y2=-2pn.

因直线MA和直线MB与x轴所成的角相等，等价于kMA+kMB=0.

而kMA+kMB=y1x1-m+y2x2-m=2ty1y2+（n－m）（y1+y2）（x1－m）（x2－m），于是2ty1y2+（n-m）（y1+y2）=2t（-2pn）+（n-m）2pt=-2pt（m+n）.

又t∈R，所以kMA+kMB=0-2pt（m+n）=0m+n=0.

故直线MA和直线MB与x轴所成的角相等的充要条件是m+n=0.

特别的，当p=1，n=2，m=-2时，就变成2018年全国Ⅰ卷文科数学第20题，即上面的变式2.类似的高考题还有2015年全国Ⅰ卷理科第20题，作为练习2供读者使用.

练习2 （2015年全国卷Ⅰ理科第20题）抛物线C：x2=4y与直线l：y=kx+a（agt;0）交于M，N两点. y轴上是否存在点P，当k变动时，总有∠OPM=∠OPN请说明理由.

2.3" 面积或面积的最值问题

面积或面积最值问题是常考题型，其设问形式多样，可以直接设问求三角形面积或四边形的面积、可以是三角形或四边形面积的最值、或是两个多边形的面积关系探求基本结果、或探求面积的定值问题.在计算相应多边形面积的过程中，不仅要求学生熟练掌握基本公式（如弦长公式、点到直线的距离公式、三角形面积公式、四边形面积公式等），还需要找到合适的方法来解决代数和几何之间的转换.求出面积的函数表达式后，通过基本不等式或基本初等函数的单调性或导函数解决最值问题，所以面积问题的考查也是解析几何中综合性较强的一个考点.下面我们就变式3为例，提供解决面积问题的常见方法和策略，仅供参考.

变式3" 已知C：y2=2x，坐标原点为O，M，N为C上两点，OM·ON=0，则△MON面积的最小值为4.

本题考查抛物线的基本知识，以向量数量积为条件，求解与抛物线顶点相关的三角形面积的最值，涉及到解析几何的基本思想和基本方法.该变式也是2023年高考全国甲卷理科第20题、文科第21题的题源.

解法1" "显然，直线MN的斜率不为零，设直线MN的方程为x=my+t.

联立x=my+t，

y2=2x， 消去x整理可得y2-2my-2t=0.

设M（x1，y1），N（x2，y2），由韦达定理可得y1y2=-2t，所以OM·ON=x1x2+y1y2=14（y1y2）2+y1y2=t2－2t，而由OM·ON=0，可得t=0，或t=2，显然t≠0，所以t=2.即y1+y2=2m，y1y2=-4.

点O到MN的距离d=2m2+1，而MN=（1+m2）（4m2+16）.

S△OMN=12MNd=4m2+16≥4，所以当m=0时，S△MON的最小值为4.

解法2" "以O点为极点，以x轴正向为极轴方向建立极坐标系，则y2=2x极坐标方程为：ρ2sin2θ=2ρcosθ，即ρ=2cosθsin2θ.

设M（ρ1，θ），N（ρ2，3π2+θ），故ρ1=2cosθsin2θ，ρ2=2sinθcos2θ，则S△MON=12ρ1ρ2=2sinθcosθsin2θcos2θ=2sinθcosθ=4sin2θ≥4，所以当θ=π4时，S△MON的最小值为4.

注" 解法1联立直线与圆锥曲线的方程，利用韦达定理（解析几何的通法通解）、弦长公式、点到直线的距离公式，合理设计参数并用其表示三角形面积，注意参数的取值范围（或满足的条件），是确定△MON面积最小值的关键.由于△MON的两直角边是与原点构成的距离，故方法2利用建立极坐标系，联立抛物线和直线，由韦达定理之积直接得到△MON面积的表达式，再利用三角函数的单调性求最值.

结论3" 已知C：y2=2px（pgt;0），坐标原点为O，M，N为C上两点，OM·ON=0，则△MON面积的最小值为4p2.

结论3中的p=1，即为上述变式3的特殊情况.结论3的证明完全可参照变式3的解法加以分析与处理，这里不多赘述.细品解题与证明过程，笔者发现结论值得进一步探究.我们尝试将结论3中的原点变为抛物线的另一特殊点焦点，可以得到以下另一个结论：

推广" 已知C：y2=2px（pgt;0）的焦点为F，M，N为C上两点，MF·NF=0，则△MNF面积的最小值为（3-22）p2.

证明" "以F点为极点，以x轴正向为极轴方向建立极坐标系，

则y2=2px的极坐标方程为：ρ=p1－cosθ，设M（ρ1，θ），N（ρ2，π2+θ），所以ρ1=p1－cosθ，ρ2=p1+sinθ，故S△MFN=12ρ1ρ2=12·p1－cosθ·p1+sinθ=p22·11+sinθ－cosθ－sinθcosθ，令t=sinθ－cosθ，则t∈［－2，2］，sinθcosθ=1－t22.

故S△MFN=p22·11+t－1－t22=p2t2+2t+1=p2（t+1）2，因为（t+1）2≤（2+1）2，所以S△MFN≥p2（2+1）2=（3－22）p2.

2023年高考全国甲卷理科第20题文科第21题为推广的特殊情形，即为p=2的特殊情形，利用推广立刻得到△MNF面积的最小值为12－82.下面把该题作为练习3，供读者练习强化使用.

练习3 （2023年全国甲卷理20）已知直线x-2y+1=0与抛物线C：y2=2px（pgt;0）交于A，B两点，且AB=415.

（1）求p；

（2）设C的焦点为F，M，N为C上两点，MF·NF=0，求△MNF面积的最小值.

参考文献

［1］中华人民共和国教育部制定.普通高中数学课程标准［M］.北京：人民教育出版社，2020.

［2］黄轶.正交于顶，隐含定点——基于一道教材习题的探究与拓展［J］.中学数学，2023（21）：11-12.

［3］王东海.2023年高考甲卷理数解析几何大题的深入探究［J］.中学数学研究（华南师范大学），2023（17）：11-13.

［4］方勇，孙要强.基于深度学习的“解析几何中的定点与定值问题”微设计［J］.中学数学教学参考，2021（10）：68-70.