动手尝试 分类验证

在小学阶段，我们借助剪拼三角形纸片的三个内角，发现任意三角形的内角和都是180°。最近，随着我们学习了“平面图形的初步认识”这一章，我了解到了多边形的概念：在平面内，由不在同一条直线上的三条或更多线段首尾顺次相连形成的封闭图形被称为多边形。这让我产生了一个疑问：多边形的内角和是否还是180°呢？如果不是，那么它的内角和又与哪些因素有关系呢？带着这样的疑问，我开始了探索之旅，并找到了答案。现在，我迫不及待地想与大家分享我的探索过程。

我先对四边形ABCD的内角和进行了探索（如图1）。根据教材中对角线的概念，我连接对角线AC，将四边形ABCD分割成两个三角形（△ABC、△ACD）。根据三角形的内角和为180°，所以四边形ABCD的内角和为180°×2=360°。

接着，我对五边形ABCDE的内角和进行了探索（如图2）。同样，过顶点A分别连接对角线AC、AD，这样将五边形ABCDE分割成3个三角形（△ABC、△ACD、△ADE）。根据三角形的内角和为180°，所以五边形ABCDE的内角和为180°×3=540°。

通过这样的操作，我发现，对于n边形来说，过其中的一个顶点，可以作（n-3）条对角线，将n边形分割成（n-2）个三角形，再根据三角形的内角和为180°，得n边形的内角和为180°（n-2）。

上面的探索方法是从顶点构建了对角线，将多边形进行了分割。那么，能否从其他一般的点进行分割呢？我又开始了思考。

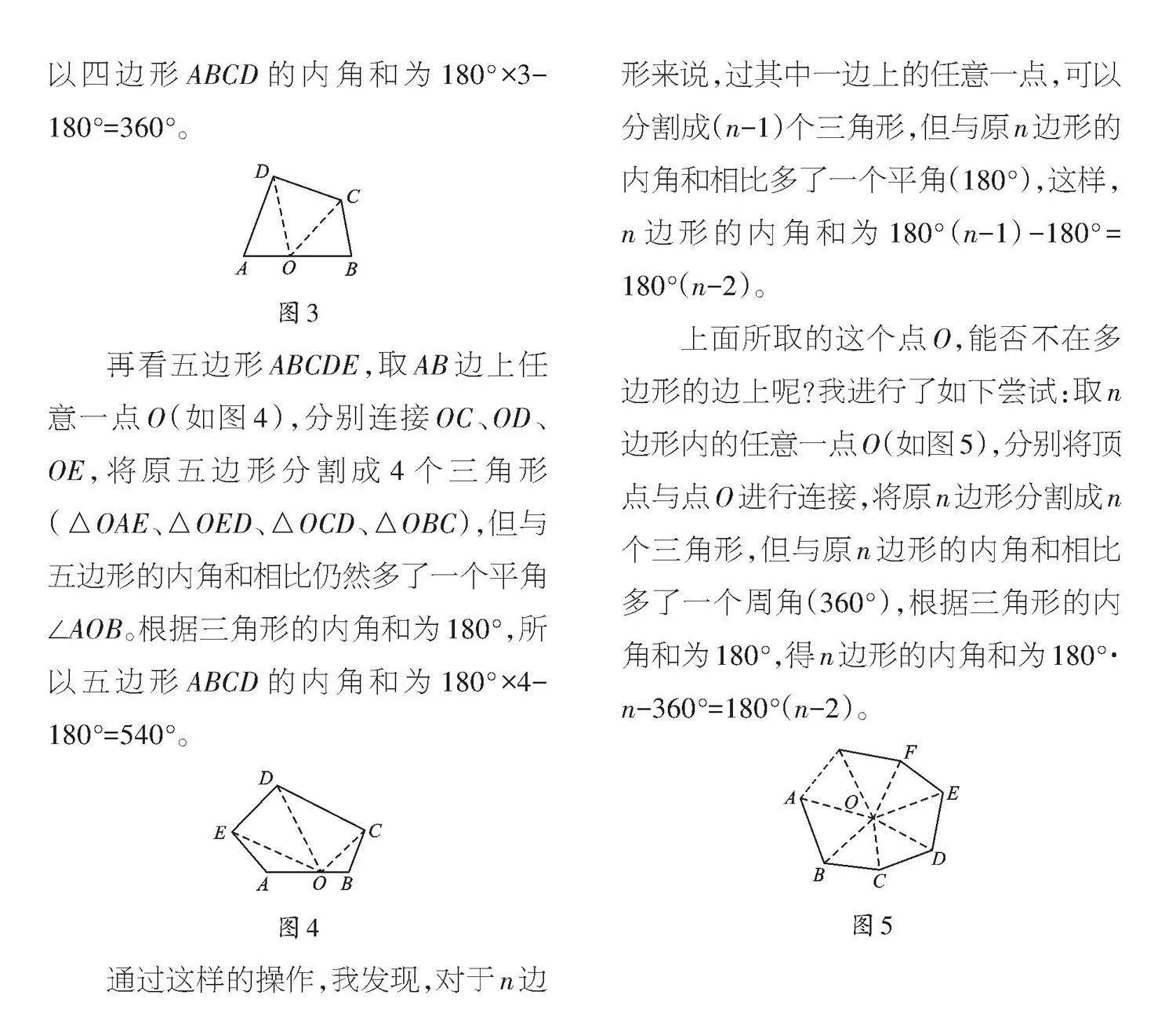
仍然从四边形入手，取四边形ABCD的AB边上任意一点O（如下页图3），分别连接OC、OD，将原四边形分割成3个三角形（△OAD、△OCD、△OBC），但与四边形的内角和相比多了一个平角∠AOB。根据三角形的内角和为180°，所以四边形ABCD的内角和为180°×3-180°=360°。

再看五边形ABCDE，取AB边上任意一点O（如图4），分别连接OC、OD、OE，将原五边形分割成4个三角形（△OAE、△OED、△OCD、△OBC），但与五边形的内角和相比仍然多了一个平角∠AOB。根据三角形的内角和为180°，所以五边形ABCD的内角和为180°×4-180°=540°。

通过这样的操作，我发现，对于n边形来说，过其中一边上的任意一点，可以分割成（n-1）个三角形，但与原n边形的内角和相比多了一个平角（180°），这样，n边形的内角和为180°（n-1）-180°=180°（n-2）。

上面所取的这个点O，能否不在多边形的边上呢？我进行了如下尝试：取n边形内的任意一点O（如图5），分别将顶点与点O进行连接，将原n边形分割成n个三角形，但与原n边形的内角和相比多了一个周角（360°），根据三角形的内角和为180°，得n边形的内角和为180°·n-360°=180°（n-2）。

教师点评

胡孙龙同学在探索知识的过程中，能够积极思考，灵活应用所学的数学知识对发现的问题进行深入探究。他经历了从特殊到一般的归纳、猜想、验证的过程，不仅通过一题多解不断地进行自我反思，还对问题进行有深度的思考与拓展，展现了他在数学学习上的扎实基本功。

（指导教师：陈广兵）