一道质检试题的解析与解构

摘 要：笔者以武汉市部分学校高三起点质量检测的解析几何试题为例，通过探析解法源头，层层剖析问题本源，反思“一题多解”“解题规律”等途径，阐述了如何在解题活动中引导学生思考问题，如何让解题思路变得更自然，更合乎情理.

关键词：导图探路；表征化归；溯源解构

解题是数学学习中的主要活动，正如美国数学家加德纳（M.Gardner）所说，数学的真谛在于不断寻求越来越简单的方法证明定理和数学问题.值得指出的是，这里所谓的“简单”，并不是指什么特殊的技巧和书写过程的简洁，而是解决这个问题的思维过程是自然的、简单的，所用的知识是基础的.本文以真实考题为背景，从多个角度出发，探析各种解法的思路和步骤，以期对各种方法进行汇总整理，为教学提供一定的参考.

1 试题呈现

（武汉市部分学校高三起点质量检测第22题）已知椭圆E：x2a2+y2b2=1（agt;bgt;0）的离心率为22，点A（0，-1）是椭圆E短轴的一个四等分点.

（1）求椭圆E的标准方程.

（2）设过点A且斜率为k1的动直线与椭圆E交于M，N两点，且点B（0，2），直线BM，BN分别交⊙C：x2+（y-1）2=1于异于点B的点P，Q，设直线PQ的斜率为k2，求实数λ，使得k2=λk1恒成立．

关于试题的解法研究，教师都是力图寻找最合理、最自然的解题过程，这样的解题过程有益于学生理解为何这样解.学生一旦找到思维的源头，便能沿着源头顺流而下，进而得到问题的最自然解法以及对问题本质的挖掘.

2 导图探路，析题思难

题中涉及多重几何关系.由于学生运算能力的不足和分析意识的欠缺，多数学生辨不清方向陷入运算泥沼导致无功而返.因此，解题教学的首要目标在于帮助学生从具体运算中抽

身出来，在更高层面的算法框架中思考解决问题.

题目中主要条件包括由过定点A且斜率为k1的动直线与椭圆E交于M，N两点，直线BM，BN交圆C于P，Q两点，目标则是研究直线MN，PQ的斜率关系.考虑到题中涉及四个

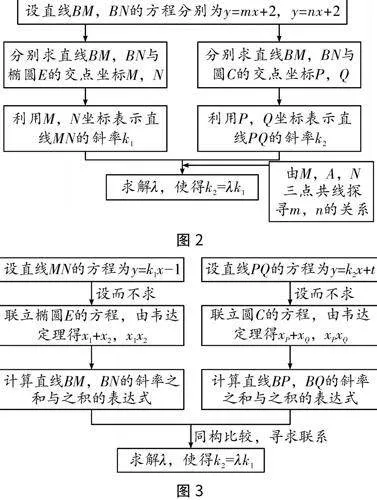
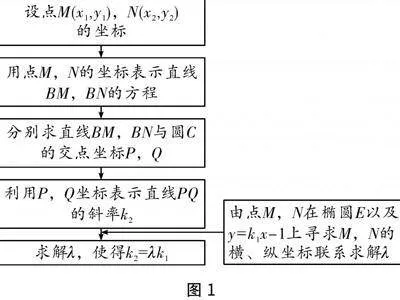
动点与四条动直线，不同的动直线设法、不同的动点设法便有不同的解题路径，剖析解题的关键节点，可以绘制出三种不同解法的思维导图（如图1、图2、图3）.

本题所有“信息”都是由“过定点A的动直线”主条件“引发”的，从以上思维导图可以发现，这个主条件的介入时序并不一致，得出约束条件并表示出点P，Q的坐标则是殊途同归；题设中涉及多个参数，因此用设定参数表示点P，Q的坐标，应用约束条件证明k2=λk1恰是运算的难点所在.正如驾车出行前需要借助导航软件设计行车路线一样，解题也需要“模拟导航”.一方面，借助导图可以变解题中的“走迷宫”为按图索骥，清楚地知晓“在哪儿”（已知条件），明晰“到哪儿去”（目标结论）；另一方面，通过导图分析确定解题方向，在已知与未知之间架设通道，从而将运算的重点落实在不断消除条件与结论之间的差异上，即“经历怎样的过程，如何到达”.在解题教学中，一方面要加强学生对知识点的学习和研究；另一方面要引导学生思考和分析问题模拟导航，让解题思路变得更自然，更合乎情理．

3 表征化归，一题多解

第（1）问易得椭圆E的标准方程为x28+y24=1.

第（2）问，如果通过绘制思维导图分析算法，那么具体解题活动则是算法优化.虽然思维导图可以做到心中有数，但解题实践中解法的修正完善（修正考试中搁浅的做法）环节进程并不“顺畅”，仅有个别学生能真正走出“围城”.为此，下面通过一题多解，帮助学生走出困境，引导学生探求问题解决的最佳方案，真正做到“对症”施策，让解题思路变得更自然，寻求到有效的解决办法，从而培养学生良好的解题习惯和解题能力.

解法1： 设M（x1，y1），N（x2，y2），P（xP，yP），Q（xQ，yQ），直线MN的方程为y=k1x-1，

则直线BM的方程为y=y1-2x1x+2，与x2+（y-1）2=1联立，得

［x21+（y1-2）2］x2+2x1（y1-2）x=0．

由xP≠0，且点B（0，2）在⊙C上，得xP=-2x1（y1-2）x21+（y1-2）2.

又x218+y214=1，即x21=8-2y21，代入上式得xP=-2x1（y1-2）8-2y21+（y1-2）2=2x1y1+6，

yP=y1-2x1xP+2=4-16y1+6，即点P

2x1y1+6，4-16y1+6，同理Q

2x2y2+6，4-16y2+6.

k2=yP-yQxP-xQ=4-16y1+6-4-16y2+62x1y1+6-2x2y2+6=8（y1-y2）x1y2-x2y1+6x1-6x2，

将y1=k1x1-1，y2=k1x2-1代入上式，

得k2=8k1（x1-x2）5（x1-x2）=85k1，

所以λ=85时，k2=λk1恒成立.

解法2：设直线BM的方程为y=mx+2，直线BN的方程为y=nx+2.

由y=mx+2，

x2+（y-1）2=1，

消去y得（1+m2）x2+2mx=0，解得xP=-2m1+m2，yP=21+m2，

则P

-2m1+m2，21+m2，同理可得Q

-2n1+n2，21+n2.

由

y=mx+2，

x2+2y2=8，

消去y得（1+2m2）x2+8mx=0，解得xM=-8m1+2m2，yM=2-4m21+2m2，

则M

-8m1+2m2，2-4m21+2m2，同理可得N

-8n1+2n2，2-4n21+2n2.

由M，A，N在一条直线上，所以kMA=kNA，则2-4m21+2m2+1-8m1+2m2=2-4n21+2n2+1-8n1+2n2，

整理得3-2m2m=3-2n2n，所以mn=-32.

又k2=21+m2-21+n2-2m1+m2--2n1+n2=n2-m2（n-m）（1-mn）=n+m1-mn=25（n+m），

k1=yM-yNxM-xN=2-4m21+2m2-2-4n21+2n2-8m1+2m2--8n1+2n2=8（n2-m2）8（n-m）（1-2mn）=n+m1-2mn=14（n+m），

所以k2=85k1，故λ=85时，k2=λk1恒成立.

解法3：设M（x1，y1），N（x2，y2），P（xP，yP），Q（xQ，yQ），直线MN的方程为y=k1x-1，直线PQ方程为y=k2x+t（t≠2）.

由

y=k1x-1，

x28+y24=1，

可得（1+2k21）x2-4k1x-6=0，则x1+x2=4k11+2k21，x1x2=-61+2k21.

kBM+kBN=y1-2x1+y2-2x2=k1x1-3x1+k1x2-3x2=2k1-3（x1+x2）x1x2=4k1，

kBMkBN=y1-2x1y2-2x2=k1x1-3x1k1x2-3x2=k21x1x2-3k1（x1+x2）+9x1x2=-6k21-12k21+9（1+2k21）-6=-32.

由

y=k2x+t，

x2+（y-1）2=1，

可得（1+k22）x2+2k2·（t-1）x+t（t-2）=0，

则xP+xQ=-2k2（t-1）1+k22，xPxQ=t（t-2）1+k22.

kBP+kBQ=yP-2xP+yQ-2xQ=k2xP+t-2xP+k2xQ+t-2xQ=2k2+（t-2）（xP+xQ）xPxQ

=2k2-2k2（t-2）（t-1）t（t-2）=2k2t.

kBPkBQ=yP-2xP·yQ-2xQ=k2xP+t-2xP·k2xQ+t-2xQ=k22xPxQ+k2（t-2）（xP+xQ）+（t-2）2xPxQ=

k22t（t-2）-2k22（t-2）（t-1）+（k22+1）（t-2）2t（t-2）=t-2t.

由

kBM+kBN=kBP+kBQ，

kBMkBN=kBPkBQ，

即

4k1=2k2t，

-32=t-2t，

解得

t=45，

k2=85k1，

所以λ=85.

数学解题中离不开表征与化归，上述解题过程虽设有多个字母变量，但因有具体的代

数表示，条件与结论间的差异一目了然，不难锁定解题方向为“消参”.由于条件和目标的联立中形成方程组意识，这样化归便简化为上下求索中确定消参的步骤.本题含有多个变量参数，考虑到目标中仅含有k1，k2，消去中间参数或寻求参数之间的联系自是应有之举，也是解题中的自然选择．

4 溯源解构，一解多题

解题教学中，教师通过拓展解题思路、发散问题的多种解法将题目讲透固然重要，但更需要把题目讲活，让学生通彻明白问题的诸多变化.挖掘试题的内涵价值，拓展试题的外延范围，从而实现做一道题、通一类题、变多道题.

由解法3，可以发现从两个角度研究了直线BM，BN的斜率之和与之积，从而解决问题.

“和”与“积”令我们联想到一元二次方程的根与系数关系，整理一下思路便有以下解法.

解法4：设直线MN的方程为y=k1x-1，直线PQ的方程为y=k2x+t（t≠2），直线BM的方程为y=k3x+2，直线BN的方程为y=k4x+2.

由

y=k1x-1，

y=k3x+2，

解得M

3k1-k3，2k1+k3k1-k3，将点M坐标代入椭圆方程x2+2y2=8，得

2k23-8k1k3-3=0.

同理，由

y=k1x-1，

y=k4x+2，

求得N

3k1-k4，2k1+k4k1-k4，将点N坐标代入椭圆方程x2+2y2=8，得

2k24-8k1k4-3=0，故k3，k4是二次方程2x2-8k1x-3=0的两根.

由

y=k2x+t，

y=k3x+2，

解得P

2-tk2-k3，2k2-tk3k2-k3，将点P坐标代入圆的方程x2+（y-1）2=1，得

t（t-2）k23-2（t-2）k2k3+（t-2）2=0.又t≠2，所以tk23-2k2k3+（t-2）=0.

同理，由

y=k2x+t，

y=k4x+2，

得Q

2-tk2-k4，2k2-tk4k2-k4，将点Q坐标代入圆的方程x2+（y-1）2=1，得

tk24-2k2k4+（t-2）=0，故k3，k4是一元二次方程tx2-2k2x+（t-2）=0的两根.

2x2-8k1x-3=0与tx2-2k2x+（t-2）=0为同解方程，所以2t=-8k1-2k2=-3t-2.

由2t=-3t-2，解得t=45.由-8k1-2k2=2t，可得k1k2=12t=58，所以k2=85k1，

故λ=85时，k2=λk1恒成立.

解法4不同于上述3种解法，它关注曲线上的点由哪两条直线相交所得，通过联立直线，求得交点坐标后代入二次曲线方程，构造关于斜率的一元二次方程来解决问题.学生习惯于直线与曲线联立后解决问题，虽然直线与直线联立也是常规之法，但直线与直线联立后代入曲线则较少为之，相较于解法3，解法4更自然，还揭示了本题的命题背景.

命题背景 已知椭圆C：x2a2+y2b2=1（agt;bgt;0），过定点A（0，t）（点A不在椭圆上）且斜率为k的直线l交椭圆C于M，N两点，点P（0，b），记直线PM，PN的斜率分别为k1，k2，则k1k2为定值；存在实数λ，使得k1+k2=λk．

解析：设直线l的方程为y=kx+t.

由

y=kx+t，

b2x2+a2y2=a2b2，

可得（b2+a2k2）x2+2a2ktx+a2（t2-b2）=0，

则x1+x2=-2a2ktb2+a2k2，x1x2=a2（t2-b2）b2+a2k2.

k1+k2=y1-bx1+y2-bx2=kx1+t-bx1+kx2+t-bx2=2k+（t-b）（x1+x2）x1x2=2bt+bk.

k1k2=y1-bx1y2-bx2=kx1+t-bx1·kx2+t-bx2=b2（t-b）a2（t+b）.

通过上述结论，可以应用前面所学的表征、化归策略于新的问题情境，同时也推动学生对前述解题模型的更深层次思考，诱发新的想法，催生新的探究.

数学解题的目的是巩固数学基础知识，落实数学基本技能，感悟数学思想方法，提升数学思维活动经验，所以对一道典型问题的多角度分析与解答应侧重于思维的整体性，让学生有机会跳出就题解题的案臼，通过算法设计剖析问题；立足思维的深刻性，比对不同解法聚焦核心环节，在算法优化中形成解题策略构建解题模型；关注思维的广阔性，在问题“源与流”的探寻中实现触类旁通，在命题网络的构建中实现趋近“一览众山小”的通透，在寻找多解的过程中突出通性、通法的辐射、迁移的作用，追求水到渠成、自然而然的解题方法．

参考文献

［1］G.波利亚.怎样解题——数学思维的新方法［M］.上海：上海科技教育出版社，2011.

［2］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

［3］孙小龙.让反思探究成为行走的方式［J］.数学通讯，2016（2）：52-54．

［4］王芝平，王敬华.让解题思路来的更自然一些［J］.数学通报，2013（2）：43-46.