基于后继运算的新定义问题的一次命题实践

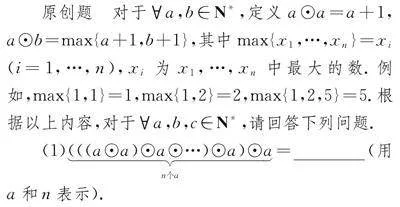
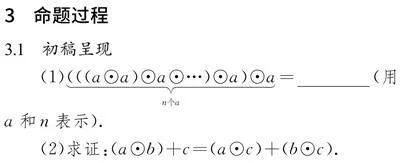
摘 要：本文以一道基于后继运算的新定义问题为例，展示命题思路及命题过程，总结命题经验与教学方法，并给出了与此背景有关的开放性的问题，以期为一线教师教学提供一些参考.

关键词：后继运算；新定义；命题实践

新定义试题是近两年来各级各类考试的热点，尤其在2024年高考中大放异彩.该题型以全新定义的数学对象或运算方式为基础，考查学生的思维能力，其形式新颖，考查功能显著，降低了盲目做题和套路训练的收益，一定程度上能起到抑制题海战术的作用，对落实数学核心素养，培养学生的创新思维也有着积极的引导作用.基于以上背景，笔者在学校高二下学期期中考试中，命制了一道基于后继运算的新定义问题，并将命题过程、试题内容、测试结果和命题反思等内容整理成文，以期为教学提供指导.

1 题目呈现

原创题 对于a，b∈N*，定义a⊙a=a+1，a⊙b=max{a+1，b+1}，其中max{x1，…，xn}=xi（i=1，…，n），xi为x1，…，xn中最大的数.例如，max{1，1}=1，max{1，2}=2，max{1，2，5}=5.根据以上内容，对于a，b，c∈N*，请回答下列问题.

（1）（（（a⊙a）⊙a⊙…）⊙a）⊙an个a=""" （用a和n表示）.

（2）满足（a⊙b）⊙c=4的有序数对（a，b，c）有几个？

（3）满足（a⊙b）⊙c=n的有序数对（a，b，c）有几个？

（4）满足（a⊙b）⊙c=a⊙（b⊙c）=n的有序数对（a，b，c）有几个？

考查目标：考查学生利用不等式和计数原理解决实际问题的能力，以及对新定义问题理解和分析的能力.

设计思路：本题是笔者为学校高二下学期期中考试命制的题目，基于已学知识，希望考查不等式、计数原理等主干内容，并渗透分类讨论、转化与化归等数学思想.同时，本题是一道以符号语言为载体的新定义问题，学生需要通过阅读材料提取信息，进而完成解答，对学生数学抽象与逻辑推理等核心素养有着较高的要求．

2 命题背景

运算等级是算术的基本概念之一，在算术运算中，根据其运算的难易程度划分的运算级别称为运算等级.例如，加法是一级运算，乘法是二级运算，乘方是三级运算.

对于上述运算，有时还采用高级运算和低级运算两个相对概念来加以区分.例如，对于一级运算来说，二级运算是高级运算，但对于三级运算来说，二级运算是低级运算.

事实上，用来描述自然数的基本性质和规律的皮亚诺公理中曾提到“后继数”，即每一个确定的自然数a，都有一个确定的后继数a′，a′也是自然数，其所代表的“后继运算”可以看成是比加法更低级的运算.这样的运算在数论以及计算机语言中也有着广泛的应用.

基于以上背景，笔者考虑将一元后继运算推广到二元和多元后继运算，以探究运算律以及得到相同运算结果的不同运算方案为目的，设计了若干题目．

3 命题过程

3.1 初稿呈现

（1）（（（a⊙a）⊙a⊙…）⊙a）⊙an个a=""" （用a和n表示）.

（2）求证：（a⊙b）+c=（a⊙c）+（b⊙c）.

（3）（a⊙b）⊙c=a⊙（b⊙c）一定成立吗？做出判断并给出证明.

（4）满足（a⊙b）⊙c=4的有序数对（a，b，c）有几个？一般地，满足（a⊙b）⊙c=n的有序数对（a，b，c）有几个？

（5）满足（a⊙b）⊙c=a⊙（b⊙c）=4的有序数对（a，b，c）有几个？一般地，满足（a⊙b）⊙c=a⊙（b⊙c）=n的有序数对（a，b，c）有几个？

（6）若a，b，c≤5，满足（a⊙b）⊙c=a⊙（b⊙c）的有序数对（a，b，c）有几个？一般地，若a，b，c≤n，满足（a⊙b）⊙c=a⊙（b⊙c）的有序数对（a，b，c）有几个？

3.2 命题思路及修改过程

在命题时，为了揭示后继运算是比加法运算更低级的运算，笔者设计了第（1）问.从运算原理上看，第（1）问的本质是多次后继运算，可以用加法运算简化；从考查目标上看，第（1）问可以引导学生通过阅读材料理解新定义运算的实际意义，为解决后续问题做铺垫.

初稿中的第（2）问和第（3）问是为了引导学生通过证明发现，该新定义运算满足分配律但不满足结合律，其推导过程会对后续复杂问题的处理带来启发.同时，其独特的性质也会引起学生探究新知的欲望，让试题活起来，激发学生学习数学的内驱力.

在磨题的过程中，组内教师讨论认为初稿中的第（2）问比较简单，且受限于试题篇幅，故将其删去.另外，由于第（4）问和第（5）问的存在，学生已经能从题干中猜到该运算不满足结合律，故初稿中的第（3）问无需单独出现，可以蕴藏在后两问中，让学生在解决问题的过程中自行发现并探究.

最终决定将初稿中第（4）问的特殊情形和一般情形分别作为定稿的第（2）问和第（3）问，既给予了学生适当的提示，也体现了从特殊到一般的数学推理方法；将初稿中第（5）问的一般情形作为定稿的第（4）问，作为对定稿第（3）问的升华，同时也作为该运算不符合结合律的一个例子，让学生在考试结束后仍有兴趣去思考和探究，希望能起到以考促学的效果，让学生实现全过程学习.

初稿中的第（6）问想说明的是，在此新定义运算的基础上，可以通过增加参与运算的变元个数或改变变元取值范围等方法，生成一系列有关问题，从而体现了该命题背景的开放性和可延展性.基于以上特征，本题可以作为教师专题教研或学生自主探究模板的题目，可起到抛砖引玉、以点及面的效果．

4 试题分析

4.1 第（1）问试题分析

分析：由题意，相同元素a与a之间每作一次⊙运算都等价于在前一次运算结果的基础上加1，n个a依先后次序共运算了n-1次，故结果为a+n-1.本题也可对a和n取特殊值，进而归纳得到结果.从阅卷情况来看，有很多学生选择这种做法.在面对新情境问题时，由特殊到一般通常是一种有效的分析方法，在日常教学中也可多向学生渗透此方法.

4.2 第（2）问试题分析

分析：借助定义中的max符号计算（a⊙b）⊙c的结果，有（a⊙b）⊙c=max{max{a+1，b+1}+1，c+1}=max{a+2，b+2，c+1}.该表达式是本题的题眼，在第（3）问和第（4）问的推理过程中也起到至关重要的作用.

（a⊙b）⊙c=4，即max{a+2，b+2，c+1}=4时，对a，b，c的取值进行分类讨论，得到（a，b，c）共有10个.在解题时，需要注意c=1或2时，对（a，b）中重复元素进行剔除.

4.3 第（3）问试题分析

分析：由第（2）问分析可知，（a⊙b）⊙c=n，即max{a+2，b+2，c+1}=n时，对a，b，c的取值进行分类讨论，得到（a，b，c）共有3n2-13n+14个.在解题时，需要注意c=1，…，n-2时，对（a，b）中重复元素进行剔除.

4.4 第（4）问试题分析

分析：借助定义中的max符号计算a⊙（b⊙c）的结果，有a⊙（b⊙c）=max{a+1，max{b+1，c+1}+1}=max{a+1，b+2，c+2}.对比（a⊙b）⊙c的结果可知，（a⊙b）⊙c和a⊙（b⊙c）不恒相等，即该运算不满足结合律.

第（4）问要解决的问题是计算（a⊙b）⊙c和a⊙（b⊙c）恰好都等于n，即满足max{a+2，b+2，c+1}=max{a+1，b+2，c+2}=n的（a，b，c）的所有可能.事实上，由第（3）问的推理过程可知，第三类中的所有情况均不成立，只需要在第一类和第二类中考虑，最终得到（a，b，c）共有n2-3n+1个.在解题时，需要注意b=1，…，n-3与b=n-2两种情况之间已经没有重复元素.

5 测试结果及分析

5.1 测试数据

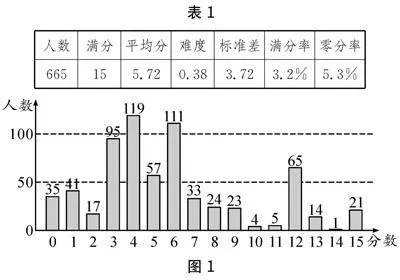
本题为本校高二下学期期中考试第17题，分值设置为“3+3+6+3”，测试对象为全体高二学生，共收到665份有效试卷.学生得分情况统计表（见表1）、各分值人数统计图如下（如图1）.

5.2 结果分析

笔者独自完成了此题的批阅工作，并结合阅卷实况和测试数据统计结果做简要分析．

5.2.1 从特殊到一般

由表1可知全体平均分为5.72，十分接近前两问的总分6分.从图1中也能够发现，有70%左右的学生只能拿到前两问以内的分数.笔者阅卷时发现，前两问都做对的学生中有很多也是使用的枚举法，缺少有条理的分类讨论流程.这种情况说明在有限的考试时间内，学生对新定义问题的处理能力还停留在表层阶段，即通过取特殊值或找规律等方法得到具体的数字结果.

该结果提示教师，在带领学生学习和探索新定义问题的解题策略时，一方面，要帮助学生掌握本题中所体现的从特殊到一般的推理方式，即通过取特殊值或找规律的方法先拿到一部分结果，从而得到一定的过程分；另一方面，需要协助学生构建从具体数字推理上升到抽象符号推理的桥梁，寻找特殊和一般之间的联系，步步为营，先敢于，再善于使用字母和符号推理，得到一般情形下的结果.在这一过程中，学生数学抽象和逻辑推理的核心素养将得到有效提升．

5.2.2 符号语言规范化

笔者将本题高分段和低分段的代表性答卷进行对比后发现，获得高分甚至满分的学生，绝大部分都能够较为规范地使用符号语言进行逻辑推理和分类讨论，其卷面整洁，运算过程和结果清晰.相反，得分较低的学生卷面书写较为随意，究其原因，可能与没有充分理解题意以及题目中所给的符号有关.

该结果提示教师，一方面，在日常课堂教学中要规范解答题的书写过程，给学生做好典范；另一方面，在带领学生进行新情境问题的专项训练时，可多换位思考，站在学生的角度与其一起剖析相关问题，引导学生善用转化与化归思想，将陌生情境化为能用熟悉的知识点解决的情境，从而实现对创新型试题的有效突破.^［1］

6 命题反思与体会

6.1 理论指导与反思

数学创新型试题是指依据数学课程标准的理念和要求，依托一定数学命题原理和技术，在题目背景、题目形式、解题方法等方面具有新颖性和独特性的数学题.数学创新型试题能够较好地诊断和培养学生的数学创新意识与能力，有效提升学生数学核心素养，在各级各类考试中都有着重要的地位.^［2］

常见的数学创新型试题包括引入新定义、融入数学史、渗透高观点等类型.本次命题成果属于引入新定义型创新试题，这类创新题的运算规则通常面向集合、向量、函数等数学对象，并选取一些不常见的特殊符号作为运算符号.学生在面对此类问题时往往具有强烈的陌生感和恐惧感，并在解题的过程中出现概念理解不透彻、运算准确度不够高等问题，究其原因，还是在数学抽象、逻辑推理、数学运算等核心素养方面有所欠缺.教师在日常教学中应重视对学生有关能力的培养.

此外，作为命题者，一方面，要在命题过程中对学生可能遇到的困难做出预判，以此为依据设置恰当的问题或做出适当的引导和铺垫；另一方面，要在题目实测后及时收集数据，与有关学生和教师交流得到反馈，从而积累命题经验，不断提升命题水准．

6.2 个人心得与体会

考试后笔者与学生交流考试感受，尤其是关于本题的想法，学生给出的反馈主要有以下两点：一是在考场上被新定义吓到，无从下手；二是考试结束后订正试卷时又觉得题目很有趣，题目本身难度不大，但是很锻炼思维能力.借此机会，笔者鼓励学生可以仿照本题自己设计新定义问题，与同学相互切磋琢磨，学生兴趣高涨，学习数学的积极性得到了提升.

经历了这次从命题、阅卷到与学生互动得到反馈，教师带领学生进行自主命题的数学探究活动的完整过程，教育形成了闭环.在这一过程中，教师拓宽了自己的专业视野，提升了自己的业务能力；学生体会到了命题者的思想，甚至自己成为命题者，感知题目的温度，在提升自身数学素养的同时，感受到数学学习的乐趣.

由此，笔者认为命题和解题不仅是教师必备的职业技能，也是教师和学生深入交流的一种方式.教师应充分利用这一方式构建与学生友好交流的纽带和桥梁，让考试结果不再是冰冷的分数，而是鼓励学生继续探索新知的动力．

参考文献

［1］沈健.赏析数学竞赛中的新定义型试题［J］.数学通讯，2022（8）：58-60+62．

［2］宋燕伶，罗荔龄，彭刚.例谈高中数学创新型试题的命制策略［J］.数学通讯，2022（24）：44-48+53．