基于GeoGebra的中职数学探究性教学的实践研究

【摘要】文章从GeoGebra软件介绍、中职数学探究性教学的必要性、GeoGebra为进行数学探究性教学提供便利、准备自主探究教学的教室、基于GeoGebra的中职数学性探究教学的实践五方面阐述基于GeoGebra的中职数学探究性教学的实践研究。

【关键词】GeoGebra；中职数学；探究性教学；对数函数

随着时代的发展与科技的进步，利用信息技术辅助数学教学的手段和案例是时代的必然趋势。GeoGebra作为现代化的教学工具之一，它操作比较简单，对于教师展示教学内容十分合适，并且能帮助学生进行自主探究，以及教师与学生之间的互动交流。GeoGebra以其免费动态、功能强大、易于操作等优点成为越来越多的教师辅助教学的有力工具。而探究性教学是以学生为中心，以教师为指导的教学方式。将GeoGebra用于中职数学探究性教学，能有效地融合二者优点，激发学生学习欲望，刺激学生的直观感受，使枯燥乏味的数学课堂变得生动有趣，提高教学效率[1]。为此，结合具体的教学案例进行分析。

一、GeoGebra软件介绍

GeoGebra软件是美国佛罗里达州亚特兰大的数学教授Markus Hohenwart于2002年设计开发的，是一款免费动态数学教学软件[2]。它由两部分组成的，即 “Geometry”＋“Algebra”，也就是形（几何）和数（代数）的完美融合，凡是数形结合的东西都可以在GeoGebra中制作，并能动态的演示。

GeoGebra软件主要有以下特点：免费软件，资源共享。GeoGebra是基于Java程序编写的，支持多平台的应用，用户可以在手机、电脑、浏览器上查阅或操作，为技术的交流和资源的共享提供了极大的便利。操作简单，易于上手。GeoGebra界面丰富可以直接使用工具栏，也可以输入命令（中英文指令都支持），输入中文命令时，自带联想补全功能，显示与输入文字接近的命令。功能强大，动态演示。GeoGebra将几何作图、代数运算和数据处理等功能融于一体兼具函数与集合、概率与统计、工作表与图表、向量与矩阵计算等功能[1]，几乎可以完成从启蒙教育到大学教育中的所有的数学教学，也可应用物理、化学等多种学科，对于56种语言都能够提供支持。GeoGebra作图实现了动态化，且具备三维功能，输入命令即可快捷地构建出图形，还可动态演示图像的生成和展开过程，真正做到“所见即所得”。

二、中职数学探究性教学的必要性

中等职业学校数学课程是中等职业学校各专业学生必修的公共基础课程，承载着落实立德树人根本任务、发展素质教育的功能，具有基础性、发展性、应用性和职业性等特点。有效的数学学习活动不能单纯依赖模仿和记忆，动手实践、自主探究与合作交流是学生学习数学的重要方法。探究性学习已经成为基础课程教学的基本要素。目前，中职数学课堂学习方式较为单一、被动，缺少自主探索合作学习的氛围；教师对学生探究精神和实践能力的培养有待提高[3]。《中职数学课程标准（2020年版）》强调学生要“积累一定的数学实践经验、增强创新意识”，学生的实践经验是在运用知识解决问题的实践活动中积累发展的，学生的创新意识是在主动探索知识的过程中得到增强的，课堂教学应该是学生积累实践经验和增强创新意识的主阵地。因此，进行数学探究性教学的实践意义重大。

三、GeoGebra为进行数学探究性教学提供便利

动态变化和数形结合是数学两种重要思想，近年来教学中常用几何画板来辅助教学，但是几何画板的基本原理是尺规作图，重点用于辅助平面几何教学，在某些内容的教学上有一定的局限性，比如圆锥曲线和立体几何中的图形就很难用几何画板作出，另外对一些稍微复杂的图形，作图过程极其复杂，不利于学生理解。而GeoGebra可以很好地解决这个问题，它所独具的动态变化和丰富的作图功能为培养学生的数学核心素养创造了条件，也为在教学过程中合理运用信息技术促进数学探究性活动的开展提供了极大的便利。

四、准备自主探究性教学的教室

如果在普通的多媒体教室使用GeoGebra教学，可配备25或50台ipad（每台都安装上GeoGebra）保证每两位或一位学生一台；也可以在计算机多媒体理实一体化实训室进行教学，同样50台计算机上都安装上GeoGebra，只有这样学生才可以自主实践、自主探究。以上是利用GeoGebra在中职数学教学中培养学生自主探究学习能力的硬性要求。

五、基于GeoGebra的中职数学探究性教学的实践

对数函数是中职数学学习的比较困难的一个知识点，画图不够精确与方便，缺乏空间想象力等，很多学生都在这一部分学得非常吃力，甚至失去了对数学学习的信心，所以如何把对数函数这一部分教得通俗易懂是一件很有意义的事情。本文以典型案例“对数函数”为例，教师首先创设教学情境，激发学生的探究兴趣，然后根据教学内容，设计探究任务，驱动学生自主探究，动手操作，从而由浅入深地理解所学，提高课堂学习效率[4]。

教学过程：创设情境

情境：已知某种细胞分裂时，由１个分裂成２个，２个分裂成４个，4个分裂成8个……得到的细胞个数y是分裂次数x的函数，这个函数表示为y=2x，x∈N*.反过来，如果我们知道细胞个数，如何得到细胞分裂的次数呢？进一步，分裂次数x是细胞个数y的函数吗？

教师：引导学生联系实际进行思考。

学生：探究题目，发现规律，写出函数解析式。

由于细胞个数y是分裂次数x的函数，这个函数表示为y=2x，x∈N*。由对数的定义可知，分裂次数x与细胞个数y之间的关系可以写为x=log2y。

因为我们习惯用x表示自变量，y表示函数，因此将这个函数写成y=log2x。

引导学生观察函数的特征：含有对数符号，底数是常数，真数是变量，从而得出对数函数的定义：函数y=logaxa＞0且a≠1叫作对数函数，由“零和负数没有对数”可知，对数函数的定义域为（0，+∞）。

引导探究

教师：研究基本初等函数的性质和步骤？

学生：①画出函数的图像；②研究函数的性质。

教师：画对数函数的图像是否需要分类？

学生：按a＞1和0＜a＜1分类讨论。

教师：观察图像主要看哪些特征？

学生：从图像的形状、位置、单调性、奇偶性、定点等角度去观察分析。

教师：接下来从不同维度共同探究对数函数的图像和性质。

实践探究

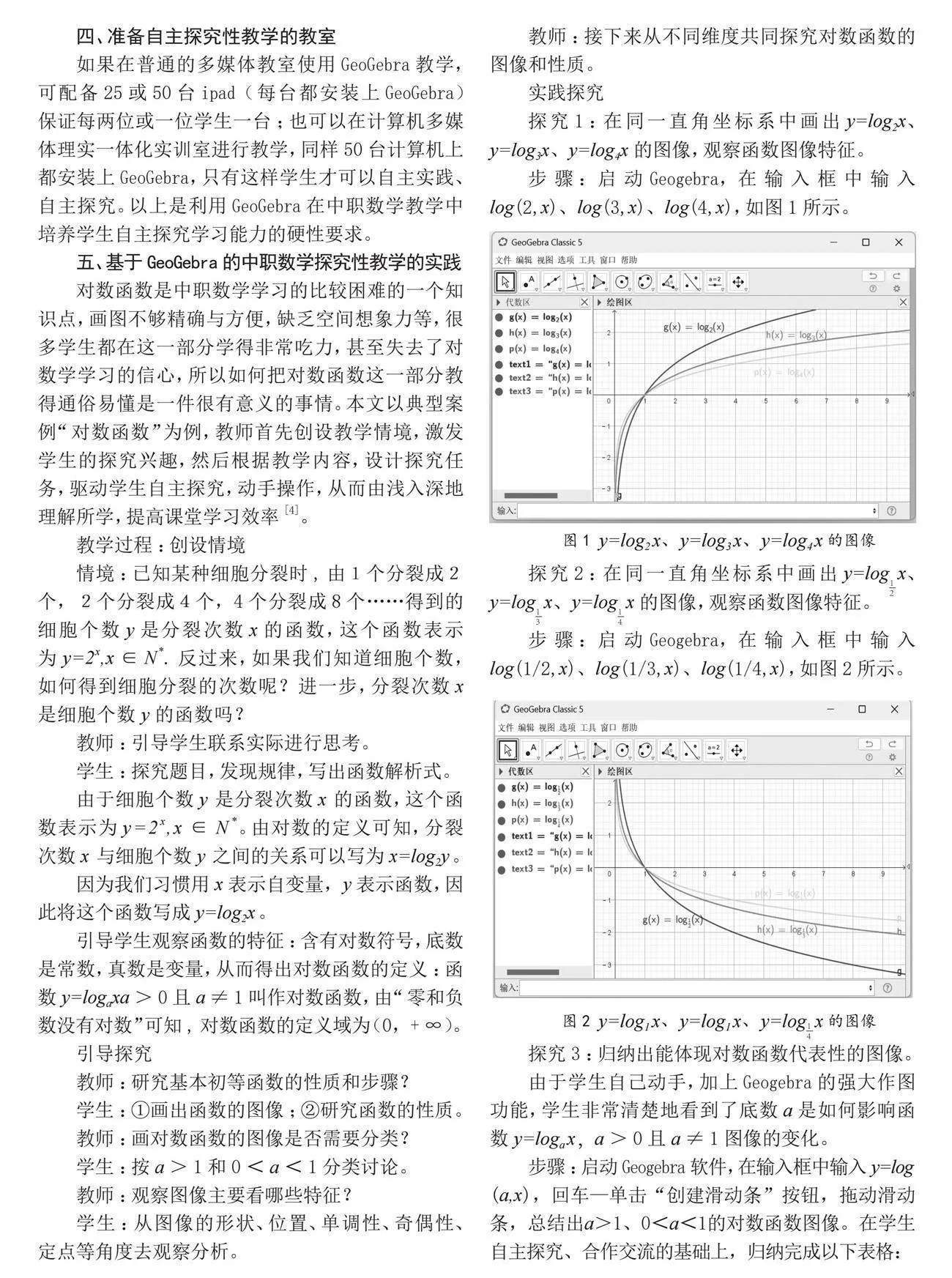
探究1：在同一直角坐标系中画出y=log2x、y=log3x、y=log4x的图像，观察函数图像特征。

步骤：启动Geogebra，在输入框中输入log（2，x）、log（3，x）、log（4，x），如图1所示。

图1 y=log2x、y=log3x、y=log4x的图像

探究2：在同一直角坐标系中画出y=logx、y=logx、y=logx的图像，观察函数图像特征。

步骤：启动Geogebra，在输入框中输入log（1/2，x）、log（1/3，x）、log（1/4，x），如图2所示。

图2 y=log1x、y=log1x、y=logx的图像

探究3：归纳出能体现对数函数代表性的图像。

由于学生自己动手，加上Geogebra的强大作图功能，学生非常清楚地看到了底数a是如何影响函数y=logax，a＞0且a≠1图像的变化。

步骤：启动Geogebra软件，在输入框中输入y=log

（a，x），回车—单击“创建滑动条”按钮，拖动滑动条，总结出a＞1、0＜a＜1的对数函数图像。在学生自主探究、合作交流的基础上，归纳完成以下表格：

（1）比较下列各题中两值的大小。

log30.7 log30.8； log0.234 log0.235；

log0.23 log34；

（2）求下列函数的定义域：

①y=log2（x−5）； ②；

在整个教学过程中，学生通过在GeoGebra作图切切实实证明了对数函数的图像，通过动态演示感受到了底数对于函数图像的影响，通过自主探究、自主学习，观察归纳整理得出对数函数的性质，并通过学以致用加深了知识的理解与运用。计算机技术的运用不仅增强了学生学习数学的积极性，又提高了学生的数学素养和信息计算素养。

综上所述，借助GeoGebra开展中职数学探究性教学，不仅使原本抽象单调的课堂变得活跃丰富、有趣，也使抽象的数学概念变得直观、生动，大幅提升了课堂效率、教学质量和学生学习数学的兴趣；希望本文能够为推进中职数学探究性教学课程改革提供一个路径，也为中职数学教师借助GeoGebra改进教学实践提供一些参考。

【参考文献】

[1]朱亮卫.基于GeoGebra的高中数学探究式教学研究[D].汉中：陕西理工大学，2020：1.

[2]钱文涛，赵军.Geogebra软件让数学教学如虎添翼[J].中国教育技术装备，2014（02）.

[3]蔡进.基于GeoGebra的中职数学探究教学的实践探索[D].扬州：扬州大学，2019：1.

[4]樊辉荣.高中数学探究性教学的实施策略[J].新课程，2020（33）.

【项目课题】珠海市教育科研2023年度市规划课题“基于GeoGebra的中职数学探究性教学的实践研究”（课题编号：2023ZHGHKT005）阶段性成果之一。