锚杆静压桩贯入特性影响因素研究

摘要

锚杆静压桩是地下工程领域应用较多的桩型之一。为了研究锚杆静压桩贯入特性影响因素，基于有限元法，建立了锚杆静压桩贯入土体三维有限元模型，利用耦合欧拉-拉格朗日（CEL）方法，考虑了桩土摩擦系数﹑土体黏聚力﹑土体弹性模量对锚杆静压桩压桩力的影响，为对比不同因素的影响程度，开展因素敏感性分析。结果表明，压桩力随桩土摩擦系数增大而增大，贯入深度会影响压桩力增加幅度，摩擦系数为0.3～0.4时与0.2～0.3时相比，压桩力增加幅度较小;压桩力随土体黏聚力增大而增大，压桩力增长幅度在20～30 kPa时大于30～40 kPa时;土体弹性模量对压桩力的影响与桩土摩擦系数规律相似，土体弹性模量为15～25 MPa时与5～15 MPa时相比，压桩力增加幅度较小，桩土摩擦系数对最大沉桩力的影响最大，土体弹性模量次之，土体黏聚力最小。

关键词

锚杆静压桩;耦合欧拉-拉格朗日法;压桩力;影响因素;敏感性分析

中图分类号：TU473.1 ""文献标志码：A ""文章编号：1004-0366（2024）06-0019-06

锚杆静压桩是地下工程领域应用较为广泛的桩型之一，锚杆静压桩法具有施工设备简单、方便、无噪声等优点，所以锚杆静压桩多用于既有建筑物增设地下空间、地基基础加固、地下室上浮治理、断柱顶升纠偏等工程［1］。贾强等［2］证明了锚杆静压桩技术应用于既有建筑物增设地下空间的可行性;文颖文等［3］采用锚杆静压桩技术，在某办公楼地下室成功增设地下车库，建筑物后续沉降满足规范要求。

随着计算机算力水平的提高，许多学者利用有限元法来分析静压法沉桩机理，如张明义等［4］采用ANSYS软件对静力压桩的沉桩过程进行数值模拟，通过算例与模拟结果对比证明研究中提出的位移贯入法能够很好地模拟静力压桩的沉桩过程;桑松魁等［5］基于ABAQUS软件，采用位移贯入法和Mohr-Coulomb准则，建立了静压桩贯入黏土的有限元模型，探究静压桩沉桩过程中孔隙水压力及有效法向应力的变化规律;肖昭然等［6］利用ABAQUS软件，基于位移贯入法和Mohr-Coulomb准则，建立了砂土静压沉桩三维模型，研究沉桩过程砂土位移场和应力场;寇海磊等［7］通过ABAQUS软件，分层采用不同的屈服准则，实现了层状黏性土和砂土中静压桩的连续贯入模拟，研究了贯入过程中沉桩阻力的变化规律。

上述数值模拟研究基于传统的拉格朗日法开展分析，随着数值模拟方法的进一步发展，耦合欧拉-拉格朗日（CEL，coupled eulerian-lagrangian）法被一些学者引入到静压沉桩过程的模拟分析中。QIU等［8］通过对比分析CEL法和经典有限元法基准测试结果，提出CEL法非常适用于模拟复杂的岩土大变形问题。基于CEL法开展静压沉桩过程研究的有：THO等［9］研究了既有桩在相邻桩沉桩时产生的力学响应;KO等［10］探究了土体在开口桩贯入过程中的运动规律;魏丽敏等［11］建立了静压管桩层状土模型，分析桩周土体位移场变化规律;高振宇等［12］建立了静压钢板桩层状土模型，研究沉桩过程中沉桩阻力的变化规律;GAO等［13］考虑了雪花形桩截面形状以及桩土作用面摩擦系数对土体的塑性区域分布、位移场、应力场的影响，研究雪花形桩的三维贯入机理;张海洋等［14］求解了桩靴插桩导致的邻近桩基桩身附加弯矩及位移;郭东等［15］分析了钻井船插桩时邻近桩近桩靴面与远桩靴面受到的挤土压力变化规律;YE等［16］讨论了不同影响因素下混凝土管桩在额外水平应力作用下的响应;王庆功等［17］分析了钻井船插桩时黏土层中邻近群桩在不同参数影响下相互作用规律。

目前对静压桩的研究多集中于管桩贯入特性，而对现有锚杆静压桩的研究又多集中于其加固效果，针对锚杆静压桩贯入特性的研究鲜少。为了准确掌握静压锚杆桩的贯入特性，通过ABAQUS软件，采用CEL方法对锚杆静压桩沉桩过程中贯入特性进行模拟分析，掌握锚杆静压桩的贯入机理，可为类似工程提供借鉴。

1 基于CEL法的有限元数值分析模型

1.1 CEL法原理

在拉格朗日算法中材料不能脱离网格，当处理桩的贯入和拔出过程、滑坡泥石流、拖锚等大变形问题时，材料与网格会出现扭曲或畸变，从而使计算结果不能收敛。在欧拉算法中材料可以脱离网格自由流动，网格的空间位置不变，所以不会产生网格大变形导致计算结果不收敛的问题。CEL法结合了拉格朗日法和欧拉法的优点，即网格固定，材料可以在网格中自由流动，材料不需要完全充满网格，且CEL法在接触面的处理上，可以准确描述物体界面。

1.2 数值分析模型的建立

采用CEL法模拟锚杆静压桩贯入过程时，由于预制混凝土桩弹性模量远远大于周围土体的弹性模量，故相对于土体而言，桩体可考虑定义为离散刚性拉格朗日体。土体定义为欧拉体，欧拉体积分数（EVF，0≤EVF≤1）代表欧拉材料在网格中的填充率，EVF=0代表网格完全为空，EVF=1代表网格完全被材料填充，0lt;EVFlt;1代表网格部分由材料填充。因此，建立模型土体时，需要在模型土体上方设置一定高度“空层”，以满足桩贯入土体过程中产生隆起。有学者认为当土体深度为2倍桩长时，基本可以消除边界效应对贯入过程的影响［10，18］。由于对称性且为节省计算时间，有限元模拟中只采用1/4模型，模型土体尺寸为长2.5 m，宽2.5 m，高8 m，土体的本构模型采用摩尔-库伦（Mohr-Coulomb）准则，土体参数设置见表1，在模型土体上方设置0.5 m的空层以供土体产生隆起。桩体由桩身和桩端两部分组成，桩身为长方体（尺寸为长0.25 m，宽0.25 m，高3.7 m），桩端为棱台（上底面尺寸为0.25 m×0.25 m，下底面尺寸为0.08 m×0.08 m，高为0.3 m），侧面为等腰梯形，静压锚杆桩数值模型如图1所示。

1.3 边界条件和网格划分

锚杆静压桩是通过位移控制法模拟桩体贯入过程，选取桩顶表面的一点作为参考点，创建刚体类型的约束，在该参考点处设置速度约束条件，使桩体以一定的速度匀速贯入土体，采用提取反力的方法探求贯入过程中的压桩力（即沉桩阻力）。模型土体下表面施加X、Y、Z 3个方向的位移约束，土体侧面施加法线方向的位移约束，土体上表面自由，不施加约束。桩土接触采用通用接触，赋予切向行为 “罚”摩擦，法向行为“硬”接触，并且允许桩土在接触后分离，通用接触的设置使得沉桩过程连续进行。网格划分中，在细网格加密区域内，模型土体单元尺寸为0.05 m，在非细网格加密区域内，模型土体单元尺寸为0.5 m，土体单元类型为8节点的线性Eulerian六面体单元（即EC3D8R），具有减缩积分和沙漏控制，土体单元数为55 080个。模型桩体单元尺寸为0.05 m，单元类型为4节点三维双线性刚性四边形（即R3D4），桩体单元数为1 622个。

1.4 地应力平衡

地球表面内部的应力被称为地应力，它的产生受重力、地球自转速度变化等因素影响［19］。岩土工程变形破坏的主要原因是初始应力场，它是决定岩土工程设计和数值分析能否成功的基本条件［20］。CEL法中的地应力平衡分析需要采用关键字定义初始地应力法，此法适用于动力显示类型分析步，在ABAQUS软件中可以直接设置预定义场，根据数值计算模型的需要，分别制定黏土上表面和底部的坐标与应力值。

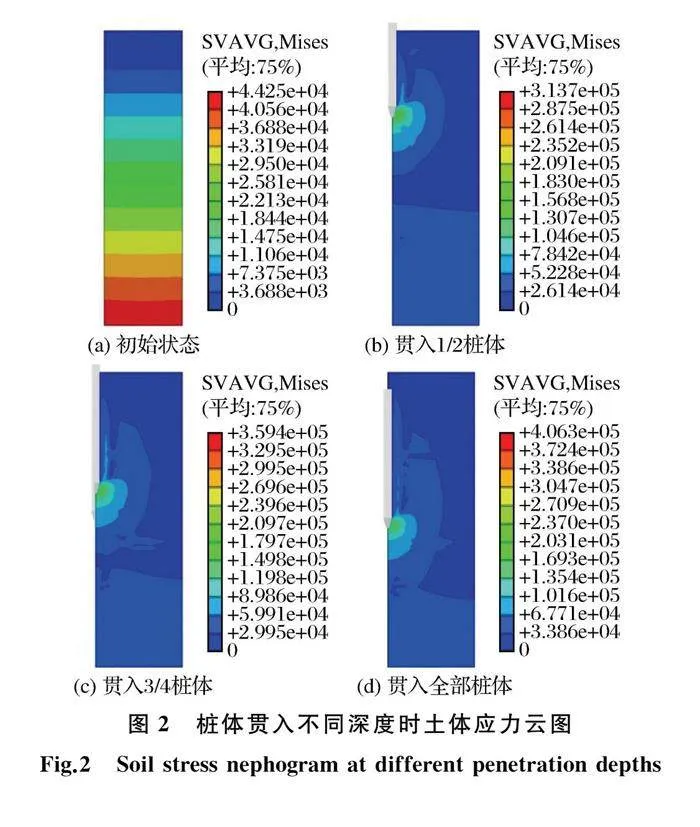
1.5 贯入不同深度土体应力

锚杆静压桩贯入土体过程为稳态贯入过程，利用已建立好的数值分析模型对土体应力变化进行分析，锚杆静压桩贯入土体一定深度时土体中应力分布情况见图2。图2（a）中初始状态即为地应力平衡后的土体应力状态，土体应力随着深度的增加而增大，由此可知，地应力平衡效果较好。随着锚杆静压桩的贯入，桩端附近出现应力泡，应力泡数值逐渐增大，土中应力受影响范围逐渐增大。

2 锚杆静压桩压桩力影响因素分析

通过已建立的数值模型，考虑了摩擦系数、土体黏聚力、土体弹性模量3个因素对静压锚杆桩压桩力的影响，分析了压桩力随桩尖贯入深度的变化规律，假定桩土摩擦系数、土体黏聚力、土体弹性模量独立于其他变量，共设置9种计算工况，各工况如表2所列。

2.1 桩土摩擦系数的影响

工况1、工况2、工况3模拟了桩土摩擦系数对压桩力随桩尖贯入深度变化规律的影响，影响结果见图3。由图3可知，随着贯入深度的增大，压桩力也逐渐增大。压桩力随着桩土摩擦系数的增大而增大，贯入深度会影响压桩力增加幅度，贯入深度不大时，桩土摩擦系数对压桩力的影响不明显，压桩力增加幅度较小，随着贯入深度的增大，桩土摩擦系数对压桩力的影响更加明显，压桩力增加幅度较大，但摩擦系数为0.3～0.4时与0.2～0.3时相比，压桩力增加幅度较小。当摩擦系数为0.2时，最大压桩力为25.61 kN;当摩擦系数为0.3时，最大压桩力为29.39 kN，较摩擦系数为0.2时增加了14.76%;当摩

擦系数为0.4时，最大压桩力为30.94 kN，较摩擦系数为0.3时增加了5.27%。压桩力随贯入深度的变化规律与文献［21］中一致。

2.2 土体黏聚力的影响

工况4、工况5、工况6模拟了土体黏聚力对压桩力随桩尖贯入深度变化规律的影响，结果见图4。由图4可知，随着贯入深度的增大，压桩力也逐渐增大。压桩力随着土体黏聚力的增大而增大，土体黏聚力为20 kPa时，最大压桩力为29.39 kN;黏聚力为30 kPa时，最大压桩力为33.49 kN，较黏聚力为20 kPa时增加了13.95%;黏聚力为40 kPa时，最大压桩力为36.45 kN，较黏聚力为30 kPa时增加了8.84%。

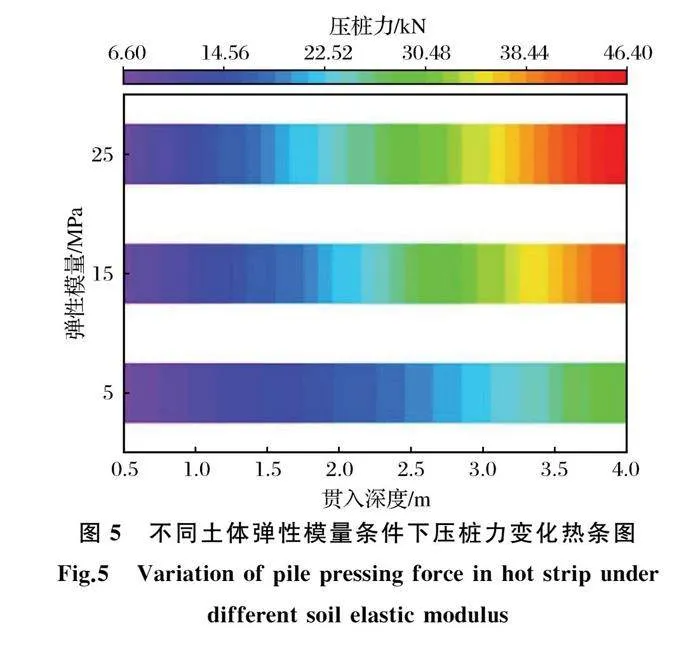
2.3 土体弹性模量的影响

工况7、工况8、工况9模拟了土体弹性模量对压桩力随桩尖贯入深度变化规律的影响，结果见图5。

由图5可知，随着贯入深度的增大，压桩力逐渐增大。压桩力随着土体弹性模量的增大而增大，贯入深度影响压桩力增加幅度，贯入深度不大时，土体弹性模量对压桩力的影响不明显，压桩力增加幅度较小，随着贯入深度的增大，土体弹性模量对压桩力的影响更加明显，压桩力增加幅度较大，但土体弹性模量为15～25 MPa时与5～15 MPa时相比，压桩力增加幅度较小。土体弹性模量为5 MPa时，最大压桩力为29.39 kN;弹性模量为15 MPa时，最大压桩力为41.74 kN，较弹性模量为5 MPa时增加了42.02%;弹性模量为25 MPa时，最大压桩力为46.25 kN，较弹性模量为15 MPa时增加了10.8%。

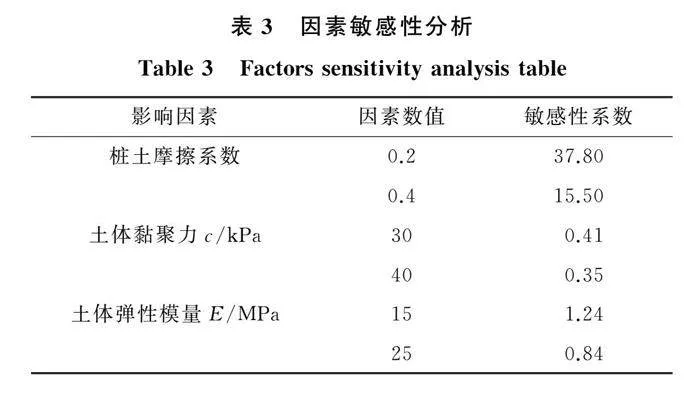
2.4 因素敏感性分析

以上考虑了不同因素对锚杆静压桩压桩力的影响，为对比不同因素的影响程度，开展因素敏感性分析。由于对多个因素进行了模拟，各因素的单位不同，因此需要进行无量纲化处理，用来比较压桩力对各因素的敏感程度，敏感性系数越大，代表压桩力对该因素越敏感。以桩土摩擦系数0.3，黏聚力20 kPa，弹性模量5 MPa为基准值，敏感性系数公式为

a=ΔFF/ΔXX， （2）

其中：a为敏感性系数;F为基准指标计算值;ΔF为某一个因素变动后指标计算值与基准指标计算值之差;X为影响因素值;ΔX为影响因素变动值。

由公式（2）计算得到因素敏感性系数，结果如表3所列。由表3可知，压桩力对各个影响因素的敏感程度为：摩擦系数＞弹性模量＞黏聚力，从单一影响因素来看，增大影响因素数值并不能增大敏感性系数，有时反而会减小敏感性系数。

3 结论

基于有限元软件，建立了锚杆静压桩贯入土体的三维有限元模型，利用CEL法对不同参数条件下锚杆静压桩的压桩力进行了分析，得到以下结论：

（1） 压桩力随桩土摩擦系数的增大而增大，贯入深度会影响压桩力增加幅度，贯入深度不大时，桩土摩擦系数对压桩力的影响不明显，压桩力增加幅度较小。随着贯入深度的增大，桩土摩擦系数对压桩力的影响更加明显，压桩力增加幅度较大，摩擦系数为0.3～0.4时与0.2～0.3时相比，压桩力增加幅度较小。压桩力随着土体黏聚力的增大而增大，20～30 kPa压桩力增长幅度大于30～40 kPa压桩力增长幅度。

（2） 土体弹性模量对压桩力的影响与桩土摩擦系数规律相似，压桩力随着土体弹性模量增大而增大，贯入深度会影响压桩力增加幅度，贯入深度不大时，土体弹性模量对压桩力的影响不明显，压桩力增加幅度较小。随着贯入深度的增大，土体弹性模量对压桩力的影响更加明显，压桩力增加幅度较大，土体弹性模量为15～25 MPa时与5～15 MPa时相比，压桩力增加幅度较小。为对比不同因素的影响程度，开展因素敏感性分析，结果表明桩土摩擦系数对最大沉桩力的影响最大，土体弹性模量次之，土体黏聚力影响最小。

参考文献：

［1］ 张明义.静力压入桩的研究与应用［M］.北京：中国建材工业出版社，2004.

［2］ 贾强，应惠清，张鑫.锚杆静压桩技术在既有建筑物增设地下空间中的应用［J］.岩土力学，2009，30（7）：2053-2057，2090.

［3］ 文颖文，胡明亮，韩顺有，等.既有建筑地下室增设中锚杆静压桩技术应用研究［J］.岩土工程学报，2013，35（增刊2）：224-229.

［4］ 张明义，邓安福，干腾君.静力压桩数值模拟的位移贯入法［J］.岩土力学，2003，24（1）：113-117.

［5］ 桑松魁，张明义，白晓宇，等.黏土地基静压桩贯入机制模型试验与数值仿真［J］.广西大学学报（自然科学版），2018，43（4）：1499-1508.

［6］ 肖昭然，郝友超，蒋敏敏，等.砂土中静压桩挤土效应的研究［J］.河南理工大学学报（自然科学版），2019，38（6）：126-133.

［7］ 寇海磊，张明义，张吉坤.层状粘性土及砂土地基中静力压桩连续贯入的数值模拟［J］.工程力学，2012，29（12）：175-181.

［8］ QIU G，HENKE S，GRABE J.Application of a coupled eulerian-lagrangian approach on geomechanical problems involving large deformations［J］.Computers amp; Geotechnics，2011，38（1）：30-39.

［9］ THO K K，CHEN Z，LEUNG C F，et al.Enhanced analysis of pile flexural behavior due to installation of adjacent pile［J］.Canadian Geotechnical Journal，2014，51（6）：705-711.

［10］ KO J，JEONG S，LEE J K.Large deformation FE analysis of driven steel pipe piles with soil plugging［J］.Computers amp; Geotechnics，2016，71（1）：82-97.

［11］ 魏丽敏，李双龙，杜猛，等.基于CEL法的静压管桩挤土效应数值分析［J］.华南理工大学学报（自然科学版），2021，49（4）：28-38.

［12］ 高振宇，李宇航，杨雪强，等.基于CEL法的静压钢板桩端阻与侧阻分析［J］.土工基础，2023，37（1）：83-87.

［13］ GAO L，LU D，QIAN J B，et al.Study on three-dimensional penetration mechanism of snowflake pile［J］.Soil Dynamics and Earthquake Engineering，2023（175）：108223.

［14］ 张海洋，刘润，贾沼霖.自升式平台插桩对邻近平台桩基础的影响研究［J］.岩土工报学报，2021，43（5）：867-876.

［15］ 郭东，王建华，范怡飞.桩靴贯入黏土层时邻近桩挤土压力分析［J］.岩土工程学报，2019，41（11）：2061-2070.

［16］ YE M G，DONG J M，ZHOU M，et al.Responses of fresh concrete piles induced by pipe pile casing penetration in clay［J］.Proceedings of the Institution of Civil Engineers-Geotechnical Engineering，2020，174（1）：58-74.

［17］ 王庆功，王建华，范怡飞.桩靴贯入黏土层时邻近群桩相互作用分析［J］.海洋工程，2021，39（2）：32-43.

［18］ PHUONG N T V，VAN TOL A F，ELKADI A S K，et al.Numerical investigation of pile installation effects in sand using material point method［J］.Computers and Geotechnics，2016，73（3）：58-71.

［19］ 代汝林，李忠芳，王姣.基于ABAQUS的初始地应力平衡方法研究［J］.重庆工商大学学报（自然科学版），2012，29（9）：76-81.

［20］ 饶运章，饶睿，王柳，等.三维初始应力场在 FLAC3D 中的反演与重构实现［J］.矿业研究与开发，2014，34（1）：11-15.

［21］ 解子腾.静压沉桩全过程准静态分析［J］.河北工程大学学报（自然科学版），2016，33（2）：34-38.

Study on the influence factors of penetration characteristics

of static pressure anchor pile

PEI Donglin1，GAO Lei1，GAO Mingjun1，ZHANG Xiaojin2

（1.Key Laboratory of Ministry of Education for Geomechanics and Embankment

Engineering，Hohai University，Nanjing 210024，China;

2.Jiangsu Jianhua Construction Co.，Ltd.，Nanjing 210009，China）

Abstract

Static pressure anchor pile is one of the most commonly used pile types in the field of underground engineering.In order to study the influence factors of penetration characteristics of static pressure anchor pile，the three-dimensional finite element model of static pressure anchor pile is established.The coupled Euler-Lagrangian （CEL） method is used，the pile-soil friction coefficient，soil cohesion，and soil elastic modulus on the jacking resistance of static pressure anchor pile are considered.In order to compare the influence of different factors，the factor sensitivity analysis is carried out.The result shows that the jacking resistance increases with the increasing of pile-soil friction coefficient，the penetration depth will affect the increasing of the jacking resistance.The jacking resistance for" pile-soil friction coefficient with 0.3～0.4 increases slightly than that of the pile-soil friction coefficient with 0.2～0.3.The jacking resistance increases with the increasing of soil cohesion.The increasing of the jacking resistance under 20～30 kPa is greater than that of under 30～40 kPa.The influence of soil elastic modulus on the jacking resistance is similar to the law of pile-soil friction coefficient.The jacking resistance for soil elastic modulus with 15～25 MPa increases slightly than that of with 5～15 MPa.The pile-soil friction coefficient has the greatest influence on the maximum jacking resistance，the elastic modulus of the soil is the middle，the soil cohesion is the smallest.

Key words

Static pressure anchor pile;Coupled Euler-Lagrange method;Jacking resistance;Influencing factors;Sensitivity analysis

（本文责编：毛鸿艳）