人字形板式换热器耦合传热特性分析

摘要

以人字形波纹板式换热器为基础，建立了完整的三板双流道耦合传热模型，并进行了数值分析。结果表明：在单边流动方式下流体出现了流量分配不均的情况，在导流区较为严重，流速与流量分布规律相同，在换热区靠近触点的位置流速更大。对计算模型施加展向周期性边界条件，发现波纹板的温度分布、总传热系数与常见的单元传热相比，误差更小。因此，在进行板式换热器模拟计算时，需要考虑耦合传热。同时分析了局部努塞尔数和二次流强度的变化趋势，发现在主流方向上，局部努塞尔数和二次流强度的变化趋势基本相同，在触点位置都出现了剧烈的变化，增强了换热，因此在设计板式换热器时，可以考虑通过适当改变结构以增加触点个数来增强换热。

关键词

板式换热器;数值模拟;导流区;周期性边界条件;二次流

中图分类号：TK172"" 文献标志码：A ""文章编号：1004-0366（2024）06-0121-08

板式换热器（PHE，plate heat exchanger）是一种紧凑高效的换热设备，由于其具有换热效率高、结构紧凑轻巧、占地面积小、污垢系数低、互换性强、便于清洗维修等优点［1］，被广泛应用于石油化工、制冷暖通、食品加工、航空航天［2-3］等领域。目前，国内外学者针对板式换热器进行了深入研究，如张晶等［4］对板式换热器的整体和局部区域进行了数值模拟，为提高传热和优化波纹参数提供了依据;张瑜都等［5］比较分析了换热器在不同流量和冷热流体温差下的传热性能和阻力性能，可通过增加冷流体的流速及增加冷流体和热流体之间的温差来确保更大的传热系数，从而提升换热器的热交换性能;刘斌等［6］对酒窝型板式换热器增加了局部突起和长条突起，模拟分析表明都达到了较好的换热效果，其中增加长条突起的改进板片可以在压降几乎不变的基础上将换热系数提高10.94%;WANG等［7］提出了一种基于拓扑优化的板式换热器，采用移动渐近法（MMA）分析了优化结构的通道组成、热性能和水力性能，对拓扑结构和人字形板式换热器进行了数值模拟和实验分析，并进行了性能比较。在研究过程中也发现了板式换热器流道内存在流体分布不均的问题，如张井志等［8］研究发现在单边流换热器中，进出口连线一侧的速度更大，导致了换热效果的不均匀;HAN等［9］通过对板式换热器人字形板片进行数值模拟获得速度场，发现板片在进、出口存在着流动死区;LI［10］对钎焊板式换热器内的单相流分布进行了实验和数值研究，结果表明在U型钎焊板式换热器中，由于进口集箱内流量的突然膨胀，在靠近换热器的前几个通道流速首先增大，其余通道流速随距换热器进出口的距离增大而减小，总流量对流量分布轮廓的影响不大，但随着板数的增加，分布不均匀的情况更加严重;SALMAN等［11］对传统的β=60°/60°和β=30°/30°的波纹板换热器（CPHEs，corrugated plate heat exchangers）和改进后的波纹板换热器的流动阻力及端口不均匀分布做了比较，结果表明改进后的CPHEs的性能更高，但对泵送功率要求较高，并建立了改进后的CPHEs与常规CPHEs的f相关关联式;LI等［12］建立了板翅式换热器横流数值模型和流动不均匀条件下的二维流动分布模型，探讨了流动分布偏置和非均匀性对换热器性能和出口温度分布的影响，结果表明，非均匀性流动降低了板翅式换热器的预期性能;王良璧等［13］以双人字形板式换热器波纹通道为对象，数值模拟研究了冷侧通道导流区结构对流量分配的影响和传热特性;BECKEDORFF等［14］以油水混合物对板壳式换热器的流动和传热特性进行了实验和理论分析，利用解析模型修正了不均匀分布对总换热系数的影响，并给出了努塞尔数相关性，根据通道压降数据建立了摩擦系数的相关性;邹宏伟等［15］制造了一台直通道及半圆形截面的印刷电路板式换热器（PCHE）样机，进行了不同流量水-水过渡区下的传热与流动实验，采用经典宏观圆管传热与流动关联式获得的计算结果与实验结果有明显偏差。

常规的板式换热器在进行数值模拟时，模型只选取换热区一部分或建立冷热两侧单元传热模型，与实际换热存在一定差距。本文建立了完整的三板冷热双流道物理模型，在板片的展向施加了周期性边界条件，分析了具有周期性边界条件的速度场，比较了两种情况下的温度场以及传热系数，同时探索了板式换热器二次流强度及其与板式换热器的传热关系。

1 物理模型与数值方法

1.1 数值计算模型

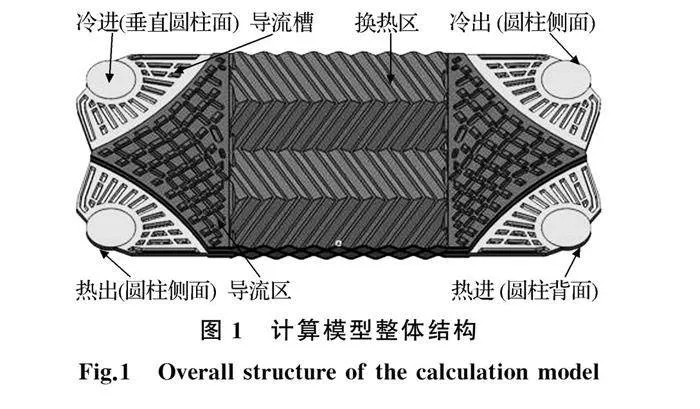
以人字形波纹板式换热器为基础，建立了三板双流道板式换热器计算模型（见图1）。模型参数：材质304钢，单板换热面积0.009 m2，波纹高度3 mm，法向节距10 mm，波纹倾角60°，波纹板厚度0.6 mm。为研究方便及节省计算资源，保留导流区及换热区板片结构，裁去进出口及导流槽板片结构。换热区展开图如图2所示。

1.2 数值方法及变量定义

使用ANSYS旗下软件Fluent进行数值模拟。冷热流体均为不可压缩的湍流流动，湍流模型采用RNG k-ε模型，近壁面采用标准壁面函数法进行处理。

采用三维笛卡尔坐标系，控制方程如下：

连续性方程表示为

ux+vy+wz=0， （1）

其中：u，v，w 分别为x，y，z方向上的速度分量（m/s）。

动量方程表示为

uUix+vUiy+wUiz=-1ρpx+μρ

2Uix2+2Uiy2+2Uiz2，（2）

其中：i为方向;Ui为i方向上的速度分量（m/s）;ρ为流体密度（kg/m3）;p为压力分量（Pa）;μ为动力黏度（Pa·s）。

能量守恒方程表示为

uTx+vTy+wTz=

α2Tx2+2Ty2+2Tz2，（3）

其中：T为温度（K）;α为流体热扩散率（m2/s）。

二次流强度的定义表示为

Se=ρw（DJx）Dμw=ρwD2μwJx， （4）

Jx=1AAωxdA， （5）

其中：A为截面面积;Jx为x方向的绝对涡量；ωx为截面法相方向涡量平均值。

1.3 边界条件

以冷流体进出口连线为X正方向，板片厚度方向为Z方向，计算所用冷流体为液态水，热流体为某低黏度流体（类乳制品），冷、热流体在流道中逆向流动，物性参数如表1所列。模型边界条件设置见表2。

1.4 数值方法验证

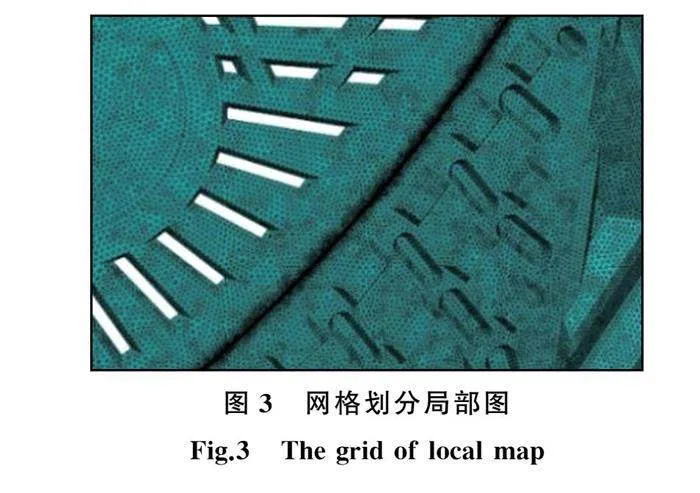
网格划分采用非结构性网格，共划分5套网格，网格数量分别为5 132 797、7 165 426、8 062 348、9 172 397、12 083 425，网格局部如图3所示。

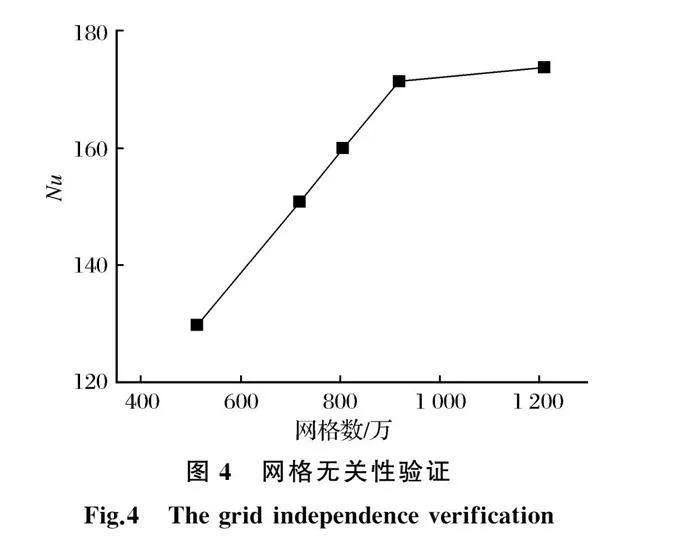
取进出口流速均为0.8 m/s进行网格无关性验证，其结果如图4所示。当网格数量为9 172 397时，平均Nu为171.25，当网格数量为12 083 425时，平均Nu为173.5，二者平均Nu误差小于0.1%，说明此时网格尺寸已达到计算精度要求。

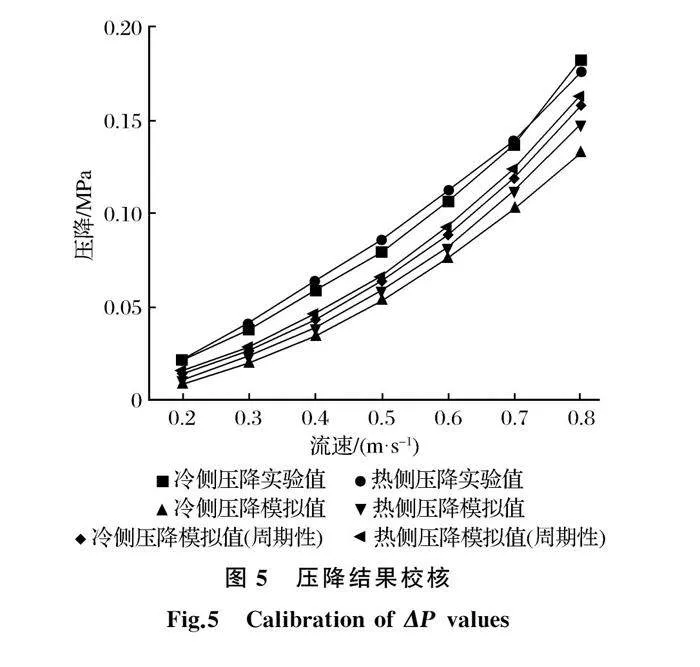
为了验证数值模拟结果的可靠性，将模拟数据与白书诚等［16］的实验结果进行对比，数值校核结果如图5所示。不同进口流速下，具有周期性边界条件的计算值相比单一的单元换热，压降更接近实验值，且冷、热流体的误差均小于10%，因此，该计算模型的结果可以反映和预测板式换热器内部传热与流动特性。

2 结果与分析

以单边流进行0.2～0.8 m/s 8种不同工况的模拟计算，并以进口流速0.8 m/s为例进行结果分析。为了更清晰直观地观察板片的传热，将模型沿着板片厚度方向（z轴）放大，如图6所示。

2.1 速度分析

图7是冷、热流体沿着主流X方向的速度云图。由图7可知，在单边流的情况下，进出口连线一侧的流体速度高于远离进出口连线一侧的流体速度，并呈阶梯状分布，而在换热区流体流速基本均匀分布。分析认为，这是由于导流区特殊的结构所致，使得流体在导流区出现了分布不均。

将冷流道换热区沿着垂直X方向间隔相同的距离作8个截面，得到垂直于X方向截面的速度云图和速度矢量局部图，如图8、图9所示。由图8和图9

可以发现，流体靠近壁面的速度小于远离壁面处的速度，这一发现符合边界层理论以及黏性效应;但接近触点位置的流体速度高于远离触点的流体速度。分析认为，这是由于流体在流经触点位置时发生剧烈的碰撞，对边界层的破坏程度较高，使得黏性效应大大降低，因此出现了流速的较大变化。

2.2 温度分析

图10为冷、热流体与中间换热板接触表面的温度分布图。由图10可以发现，冷流体在远离进出口连线一侧温升更快，热流体在远离进出口连线一侧温降更快，这一现象在导流区比在换热区更为明显。分析认为，此结果一方面是由于流动方式为单边流;另一方面是由于流体在流经导流区时，选择了通道更短，阻力更小的通道，使得在靠近进出口连线的一侧流体流动更快，流量更大。

在换热区靠近触点的位置，流体的温度变化更加明显;流体在接近触点时，流动更加剧烈，形成了大量的涡，换热更充分。换热区局部温度场及流线图如图11所示。

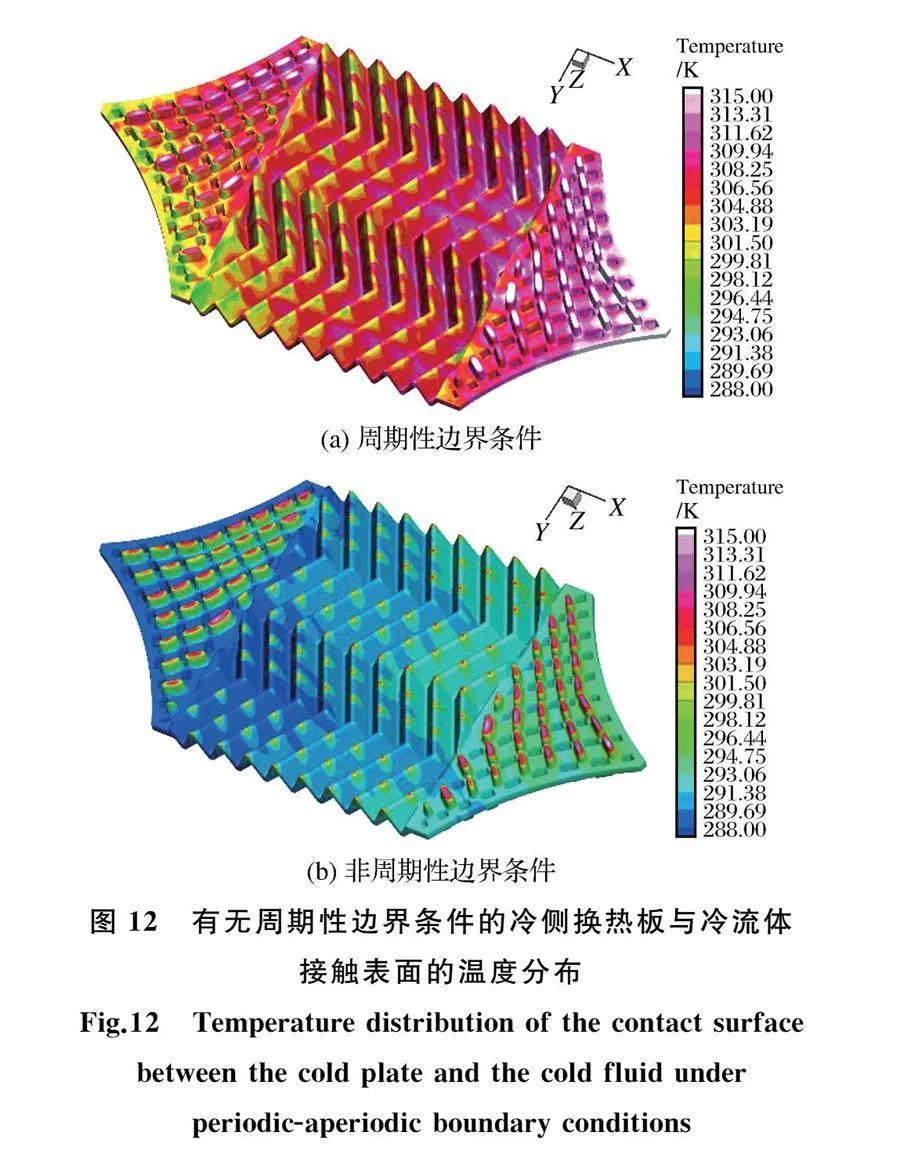
图12为有无周期性边界条件的冷侧换热板与冷流体接触表面的温度分布图。由图12可知，施加周期性边界条件的冷板与冷流体接触表面的温度相比常规的单元传热壁面湿度，平均温度提高7 K左右。

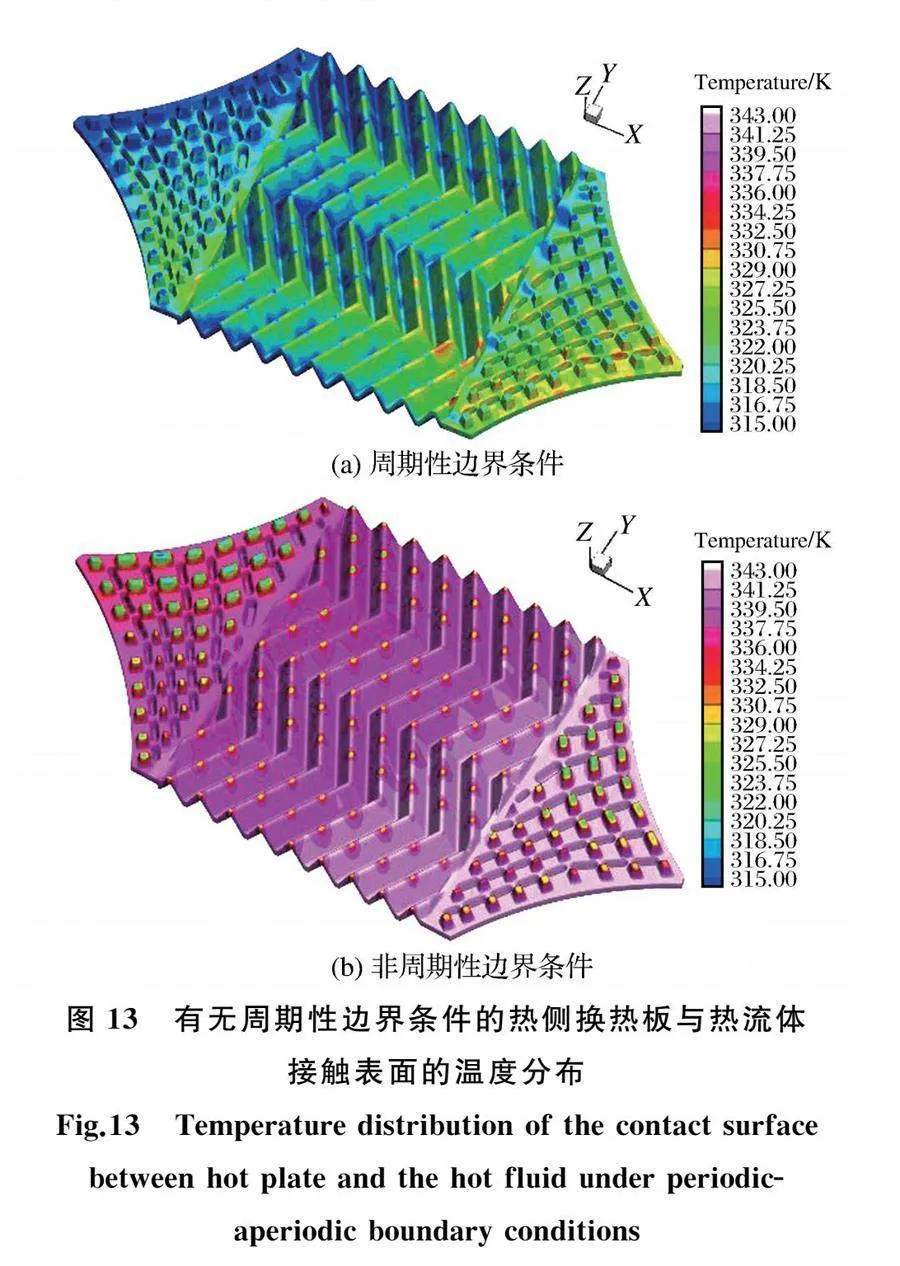
图13为有无周期性边界条件的热侧换热板与热流体接触表面的温度分布。由图13可知，施加周期性边界条件的热板靠近热流体一侧的温度相比常规的单元传热壁面，温度均有所下降，下降幅度约为6 K。

在周期性边界条件下，一侧热流体需要同时与两侧冷流体进行换热，一侧冷流体需要同时与两侧热流体进行换热，因此，冷侧温度升高，热侧温度降低。

2.3 总传热系数及Nu、Se的变化

图14为模型的总传热系数随流速的变化情况。图14显示，总传热系数随着流速的增大而增大;具有周期性边界条件的模型总传热系数小于常规的单元传热模型，但其数值却与实验值更加接近，说明具有周期性边界条件的模型能更好地反应板式换热器实际流动与传热情况。

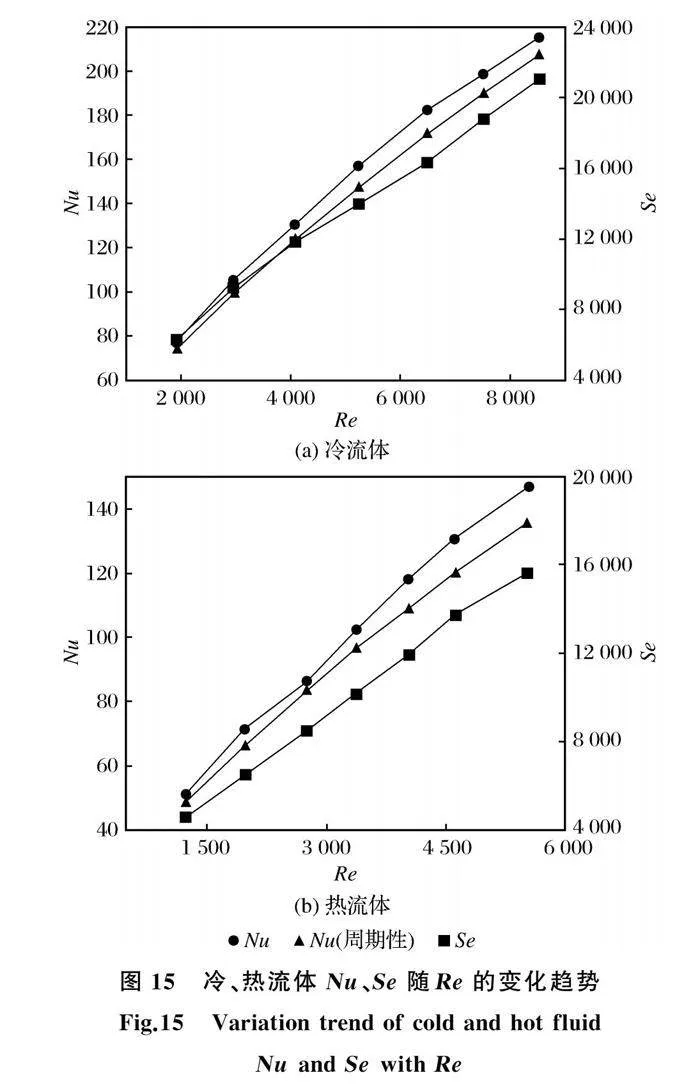
图15为冷、热流体的Nu、Se随Re的变化趋势。由图15可知，Nu、Se随Re的增大而增大;具有周期性边界条件的模型Nu略小于不具有周期性边界条件的模型。由二次流强度Se定义可知，周期性边界条件对Se并无影响。

图16为冷、热流体的Nu随Se的变化趋势。由图16可知，Nu随着Se的增大而增大，说明二次流可以强化传热，但并不完全遵循线性规律，且增长趋势基本一致。

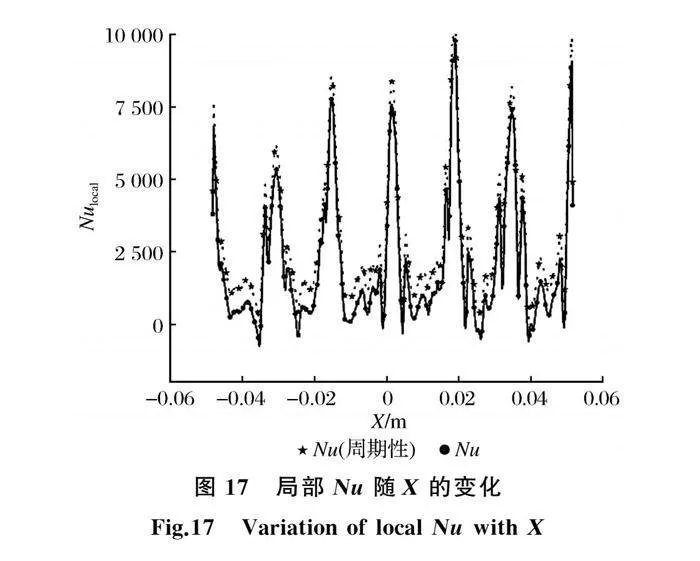
图17为冷侧壁面局部Nu随X方向的变化。由图17可知，有、无周期性两种情况下的局部Nu在数值上变化不大，在总体变化趋势上基本一致。此外，由于板式换热器的结构复杂，可以发现在触点位置的换热效果更强，因此可以考虑通过适当增加触点来强化换热。

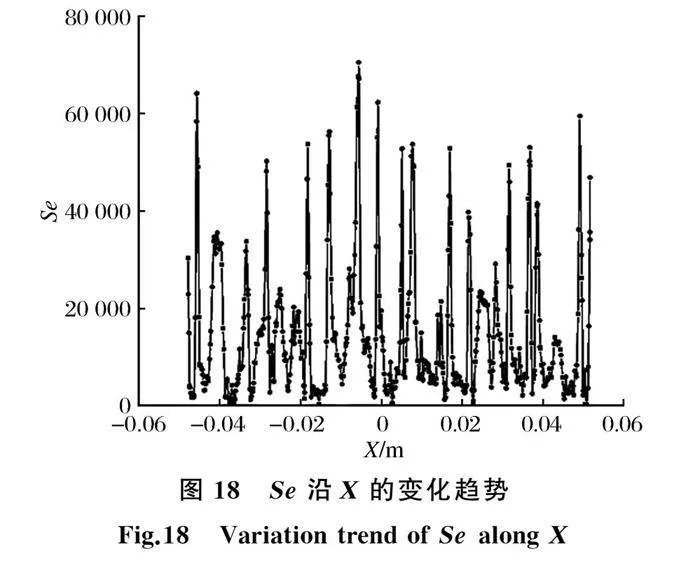
图18为Se沿X方向的变化趋势。从图18中可以看出，在主流X方向上产生了一定强度的二次流，在靠近触点的位置，产生了强烈的二次流，Se出现了峰值，然后又回归一个正常的波动范围，对比图17可知二次流强度Se和局部Nu的变化趋势具有一定的相似之处，均在触点位置发生了较大的变化。

3 结论

（1） 由于板式换热器导流区的特殊结构，在单边流方式下，出现了流量分配不均的情况;同时发现，在换热区，流体在靠近触点的位置流速更大。

（2） 比较有无周期性边界条件下冷、热流体与相应接触面的温度分布，得出在施加周期性边界条件的情况下，冷侧温度有所升高，而热侧温度有所降低。

（3） 比较有无周期性边界条件下模型的总传热系数，得出随着流速的增大，总传热系数增大，施加周期性边界条件的模型总传热系数增长速度较为缓慢。

（4） 二次流强度对板式换热器的强化传热具有比较好的效果，在触点位置，二次流强度发生了较大的变化。

参考文献：

［1］ 徐志明，郭进生，郭军生，等.板式换热器传热和阻力特性的实验研究［J］.热科学与技术，2010，9（1）：11-16.

［2］ NEAGU A A，KONCSAG C，BARBULESCU A.Calculation methods for gasket plate heat exchangers used in vegetable oil manufacture comparative study［J］.Revista de Chimie，2015，66（9）：1504-1508.

［3］ 黄莉.板式换热器波纹参数优化的数值模拟试验研究［D］.北京：北京化工大学，2010.

［4］ 张晶，文珏，赵力，等.基于计算流体力学数值模拟的板式换热器传热与流动分析及波纹参数优化［J］.机械工程学报，2015，51（12）：137-145.

［5］ 张瑜都，孔文琼.基于ANSYS FLUENT的板式换热器性能仿真［J］.工业加热，2023，52（9）：42-45.

［6］ 刘斌，耿士江，李政道，等.酒窝型板式换热器流动换热特性分析及优化［J］.暖通空调，2023，53（10）：120-125，132.

［7］ WANG D B，WU Q T，WANG G H，et al.Experimental and numerical study of plate heat exchanger based on topology optimization［J］.International Journal of Thermal Sciences，2024（195）：108659.

［8］ 张井志，田茂诚，张冠敏，等.单边流板式换热器流动换热特性［C］//第二十四届全国水动力学研讨会，2012（7）：97-103.

［9］ HAN X H，CUI L Q，CHEN S J，et al.A numerical and experimental study of chevron，corrugated-plate heat exchangers［J］.International Communications in Heat and Mass Transfer，2010，37（8）：1008-1014.

［10］ LI W Z.Single-phase flow distribution in plate heat exchangers：experiments and models［J］.International Journal of Refrigeration，2021（126）：45-56.

［11］ SALMAN A Z，SAIDUL I M，SUVASH S C.Comparison of flow resistance and port maldistribution between novel and conventional plate heat exchangers［J］.International Communications in Heat and Mass Transfer，2021（123）：105200.

［12］ LI J，GAO Y，LIU C，et al.Effect of flow maldistribution on heat transfer performance and temperature field of plate-fin heat exchangers［J］.International Communications in Heat and Mass Transfer，2023（149）：107135.

［13］ 王良璧，陈春江，雒宝明.一种板式换热器一侧流量分配的数值分析［J］.工程热物理学报，2023，44（3）：803-811.

［14］ BECKEDORFF L，SILVA R P P，MARTINS G S M，et al.Flow maldistribution and heat transfer characteristics in plate and shell heat exchangers［J］.International Journal of Heat and Mass Transfer，2022（195）：123182.

［15］ 邹宏伟，陈永东，韩冰川，等.直通道印刷电路板式换热器过渡区传热与流动的实验与数值模拟研究［J］.热力发电，2023，52（11）：140-149.

［16］ 白书诚，吴俐俊，田梦雨.波纹板式换热器传热与流动特性分析［J］.热能动力工程，2022，37（6）：114-121.

Analysis of coupled heat transfer characteristics

of herringbone plate heat exchanger

ZHU Libing1，2，WANG Liangbi1，2

（1.College of Mechanical and Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China;

2.Key Laboratory of Railway Vehicle Thermal Engineering Ministry of Education

（Lanzhou Jiaotong University），Lanzhou 730070，China）

Abstract

Based on the herringbone corrugated plate heat exchanger，a complete three-plate and two-channel coupled heat transfer model was established，and a detailed numerical analysis was carried out.The results show that the flow distribution is uneven in the unilateral flow mode，which is more serious in the diversion zone，and the flow velocity is the same as the flow distribution law，and the flow velocity is greater in the heat exchange zone near the contact.The radial periodic boundary condition is applied to the computational model，and it is found that the temperature distribution and total heat transfer coefficient of the corrugated plate are smaller than those of the common element heat transfer.Therefore，coupled heat transfer needs to be taken into account when performing plate heat exchanger simulation calculations.At the same time，the variation trend of local Nussel number and secondary flow intensity was analyzed，and it was found that in the main flow direction，the variation trend of local Nussel number and secondary flow intensity was basically the same，and there was a drastic change in the contact position，which enhanced the heat exchange.

Key words

Plate heat exchanger;Numerical simulation;Flow guide zone;Periodic boundary conditions;Secondary streams

（本文责编：毛鸿艳）