基于改进蚁群算法的生鲜配送路径优化研究

摘要

针对生鲜农产品配送路径中存在配送成本不合理的问题，以乌鲁木齐市社区菜店生鲜农产品配送为例，根据生鲜农产品新鲜度要求高、配送情况复杂的特点，优化生鲜农产品配送路径，深入分析货物运输成本、货物损耗成本以及客户对时间窗的特定要求，以此为基础，构建以综合配送成本最小化为目标的高效优化模型。为求解此模型，提出一种结合遗传算法与模拟退火机制的改进蚁群算法，旨在为生鲜农产品的配送路径优化问题提供更为精准和高效的解决方案。结合仿真实验验证模型和改进算法的有效性，对后疫情时代乌鲁木齐市社区菜店生鲜农产品配送路径优化研究提供理论基础。

关键词

路径优化;生鲜农产品;改进蚁群算法;社区菜店

中图分类号：F252.3"" 文献标志码：A"" 文章编号：1004-0366（2024）06-0108-07

后疫情时代，随着经济发展和消费水平的逐渐恢复，消费者越来越追求高水平的生活质量，因此，对于生鲜品质的要求也更加严格。生鲜农产品具有保质期短、易腐烂等不同于其他产品的特点，在考虑配送成本时要尤其注意。面对市场对于生鲜农产品的高需求，乌鲁木齐市社区菜店的产品配送、保存及销售处于一个比较尴尬的境地，如何确保消费者能购买到更加新鲜的农产品，是当前研究的一个重点问题。本次研究基于乌鲁木齐市现有社区菜店的生鲜配送路径进行优化，为营造商家和消费者双赢的局面提供一定的理论基础。

近年来国内外学者从不同方面对生鲜农产品配送路径进行研究，如YANG［1］探讨了生鲜产品生产和配送联合规划的复杂性，提出一个混合整数编程算法来优化生鲜质量和资本约束，同时建立了不对称的演化博弈仿真模型让生鲜农产品物流达到管理最优；FASANYA等［2］采用Diebold和Yilmaz溢出方法，对生鲜农产品的相互收益和被动的溢出效应进行研究。关于配送路径优化问题，很多学者都积极研究和探索，如WANG等［3］全面考虑最小配送成本，提出一种带交通影响系数的农产品配送路径优化模型；AGUSTINA等［4］综合考虑了生鲜农产品的保质期天数和交货期限，构建了带有时间窗的车辆路径问题的线性计划交叉模型；王敏荣［5］设计了一种改进遗传算法和评估指数相结合的元启发式算法，通过对比分析配送路径优化模型，旨在实现配送效率的最大化，同时确保货物的新鲜度和准时送达；葛显龙等［6］以车辆使用成本为优化目标研究带时间窗的生鲜配送路径问题，建立了相关生鲜配送路径优化模型；赵志学等［7］在研究中纳入了交通拥堵系数，构建了一个配送优化模型，该模型旨在通过最小化车辆管理成本、运输成本以及货物损耗成本，以实现配送效率的最大化；范厚明等［8］考虑模糊需求和时间窗约束，引入相关时间依赖函数，以最短配送路径为目标函数建立动态配送路径优化模型；任腾等［9］考虑交通拥堵问题，构建了以支出费用最小化为目标的路径优化数学模型；王玖河等［10］引入模糊时间窗约束，建立了多时间窗约束的电动冷藏车路径优化模型；尹三平［11］针对配送不及时、成本高等问题，建立了节约里程法的核算模型进行配送路径优化；鲍惠芳等［12］考虑时间窗约束、制冷和碳排放因素建立了冷链配送优化模型；康凯等［13］在构建生鲜农产品配送路径优化模型时，综合考虑时间窗约束与绿色配送理念，将碳排放机制纳入目标函数中，旨在实现配送过程的环境友好性与效率性的双重优化。

综上所述，带时间窗的生鲜农产品配送路径优化问题研究较为充分，然而，关于生鲜农产品综合配送成本的研究尚显不足，当前多数研究主要聚焦于降低车辆运输成本和提高客户满意度等方面，对于全面考量配送成本的综合性研究仍有待深入。尽管一些学者已将货物损耗成本纳入其目标函数中，但只考虑了运输途中存储环境和时间延续产生的货损成本，忽略了在每个商家点配送货物时，由于拿取货物需将货箱打开，导致货箱内温度平衡被打破，生鲜进一步腐败这一部分的货损成本，这也是生鲜农产品配送过程中不可忽略的成本，必须结合实际情况综合考虑。

本文以乌鲁木齐市社区菜店生鲜配送为例，根据生鲜农产品配送的独特性，深入分析其服务时间窗、货物运输成本、货物损耗成本等约束，以综合配送成本最小化为目标，构建相关的高效优化模型。针对这一复杂的车辆路径优化问题，提出一种遗传-模拟退火机制的改进蚁群算法，用以高效求解所构建的模型。通过优化生鲜配送路径以期为相关生鲜农产品企业降低成本，并且为客户带来实质性便利提供一定的理论基础。

1 问题描述与模型构建

1.1 问题的描述与假设

所有配送车辆由生鲜配送中心出发，按照订单的调度要求按时高效将生鲜农产品送达目的地，完成全部任务后立刻返回生鲜配送中心。为了确保模型构建符合现实，作出以下假设：

（1） 单配送中心、多客户点的单向生鲜配送情形;

（2） 车辆载运量相同且已知，不能超载;

（3） 客户需求量已知，单次需求量不超过车辆运载上限;

（4） 车辆起点和终点都为配送中心;

（5） 客户点与配送中心，客户点与客户点之间路线相通。

1.2 参数符号与变量定义

Mi：配送中心和客户集，i为客户编号，取值为i=1，2，3，…，m，配送中心编号为0；

Mk：车辆k在配送过程中服务的客户总数；

Qi：客户i的货物需求量；

Qk：第k辆车的最大荷载量；

P：生鲜农产品单位价值；

k：生鲜配送中心拥有k辆配送车辆，其中k为车辆编号；

tik：配送车辆k到达客户i的具体时间；

tok：配送车辆从配送中心出发的初始时间；

sik：配送车辆k对客户i的服务时长；

tij：客户i到客户j的配送时长；

dij：客户i到客户j的配送距离；

eti：最早服务客户i的时间；

lti：最晚服务客户i的时间；

ε：生鲜腐坏速率；

rt：时间窗惩罚函数的系数。

1.3 相关成本分析

（1） 车辆配送成本

车辆配送成本包括车辆固定费用和运行费用。

① 固定费用。

配送车辆的购买费和租赁费比较昂贵，一旦开始使用就会产生折旧损耗，这一部分费用需计入车辆固定费用中；每辆车需要一名司机送货，司机的劳务费计入车辆固定费用中。车辆固定费用表示为

A∑mk=1sign （Mk）。 （1）

若车辆k被使用，则会产生固定费用，Mk表示派遣k辆车服务一次的客户总量。车辆是否派遣表示为

sign（Mk）=1，Mk=1，2，3，…，n

0，Mk=0 （2）

② 行驶费用。

行驶费用由汽车行驶产生的燃油费来确定，假设配送车辆满载为Q，此时每公里油耗为C*，空载时每公里油耗为C0，则离开客户i载重为Qmi的车辆油耗为

c（Qmi）=c*-c0QQin+c0。 （3）

客户i到客户j的距离为dij，车辆油耗为dijc（Qmi）。假设每公里油耗B元/升，配送车辆运行过程中产生的总费用为

B∑nk=1∑mi=0∑mj=0xijkdijc（Qmi）。 （4）

综上所述车辆配送成本为

S=A∑nk=1sign （Mk）+B∑nk=1∑mi=0∑mj=0xijkdijc（Qmi）。（5）

（2） 时间窗惩罚成本

设时间窗为［eti，lti］，其惩罚成本是关于服务时间的分段函数。配送的产品提前送达时，惩罚成本较小。配送迟到可能会导致生鲜损失率增高，此时惩罚成本由固定成本f0和随时间改变的额外成本组成，迟到时间越久惩罚成本越大。当配送时间不在客户所能接受的范围内时，客户拒绝收货，此时惩罚成本为极大值N。综上，惩罚成本可表示为

Ri（ti）=N，ti≤ai

rt（ti-eti）2，ailt;ti≤eti

0，etilt;ti≤lti

f0+rt（ti-lti）2，ltilt;ti≤bi

N，tigt;bi（6）

（3） 货损成本

生鲜具有易腐的特点，易受温湿度、氧气浓度等因素的影响，在存储环境不佳的情况下，随着时间的延续，货损成本相应增加，配送车辆从配送中心到客户i的过程中，货损成本P（D1）表示为

P（D1）=∑mk=1∑ni=0yikPqi（1-e-ε1（tik-t0k）），（7）

其中：P为生鲜农产品的单价;ε1为产品运输时的腐败率。

在每个商家点配送货物时，由于拿取货物时货箱打开，导致箱内温度升高，产品腐败率增高，设产品腐败率为ε2，且ε2gt;ε1，货损成本P（D2）表示为

P（D2）=∑nk=1∑ni=0yikPQin（1-e-ε2sik）。（8）

此时，货损总成本P（D）可表示为

P（D）=P（D1）+P（D2）=∑mk=1∑ni=0yikP［qi（1-e-ε1（tik-t0k））+Qin（1-e-ε2sik）］。（9）

1.4 模型构建

目标函数：

min Z=S+∑mi=1Ri（ti）+P（D）。 （10）

约束条件：

∑mi=1qiyik≤Qk， （11）

∑nk=1yik=1，i∈1，2，3，…，m （12）

∑nk=1y0k=n， （13）

∑ni=1xi0k=1，k∈1，2，3，…，n， （14）

∑mi=0xil-∑mj=0xlj=0，l∈1，2，3，…，m（15）

∑mi=0xijk=yjk，j∈1，2，3，…，m;k∈1，2，3，…，n（16）

∑nj=0xijk=yik，i∈1，2，3，…，n;k∈1，2，3，…，m（17）

式（11）表示车辆k的最大载运量;式（12）表示每个客户只被服务一次;式（13）和式（14）表示车辆的起点和终点均为配送中心;式（15）表示车辆到客户点l服务后，必须从l点出发服务下一个客户；式（16）和（17）表示两个变量之间的关系。

2 算法设计

该生鲜农产品配送路径优化相对于普通的车辆路径问题（VRP，vehicle routing problem），需要考虑配送车辆的最大载运量限制以及严格的时间窗约束，使得车辆路径优化问题更加复杂。对于这类高度复杂化的车辆路径优化问题，若仅依赖传统的启发式算法，虽能得出可行解，但往往解的质量较差。为了提升求解性能，使用结合了强大融合性和搜索能力的蚁群算法，以有效应对这类问题。为克服蚁群算法在初期因信息素不足而导致的求解效率低下的问题，采用遗传算法生成初始解。在更新信息素浓度时，为确保从筛选出的优质解中选取最优者，引入模拟退火机制的Metropolis准则，从而提高算法的收敛速度和解的质量。

2.1 生成初始信息素分布

（1） 编码

设定配送中心编码为0，n个客户点编号为1，2，3，…，n。配送中心有k辆车，为了使所有客户点都被服务，设定染色体的长度为k+n+1。

（2） 初始化蚁群

为了避免偶然性，提高研究的可靠性，将n个客户点随机排列，根据模型的约束条件，把编码0随机放入排列中，并在排列的首尾插入编码0，在此生成一条染色体，为了获得多样化的解集，进行m次独立的求解过程，其中m代表种群的规模。

（3） 确定适应度

为了达到总配送成本最低，通过生鲜农产品配送路径优化模型实现目标函数min Z。根据染色体存活率与适应度函数的关系得出对应的适应度函数，具体表示为

f=1min Z。 （18）

（4） 改进选择操作

为了保证每代最优的基因不被丢失，在轮盘赌选择法中引入稳态复制原则，使其直接进入下一轮迭代。

（5） 交叉选择操作

在遗传算法中，对于交叉个体而言，需经历一个迭代选择过程，其中每一轮均随机生成一个数r。若该数r低于预设的交叉概率阈值pcc，则执行双点交叉遗传操作，此过程特别指定某一父本链作为上一代优化解的代表。然而，直接应用交叉机制可能会引发不可行解的生成，例如，在父代A（98|765432|10）与B（01|234867|59）间实施交叉后，可能产生子代A1（98|234867|10）与B1（01|765432|59），其中A1显示了基因8的重复及基因5的缺失，而B1则相反。为规避此类问题，在算法设计时采取以下措施，例如，获取A1时，可策略性地保留父代A的首尾基因段（即98与10），在B中将A中保留的基因去除，此时，B剩下B（234675），则A1为9823467510，B1同理可得。

（6）变异操作

按照概率pv对交叉选择操作的结果进行变异处理，并采用SWAP局部操作方法进行改进。

（7） 生成初始信息素分布

当迭代次数达到上限Gmax时终止迭代，此时的解看作后续算法的初始解，初始信息素浓度计算公式为

τij=∑mk=1QLk， （19）

其中：Q为信息素增强常数系数：Lk为蚂蚁k在该轮次迭代中的行走总长。

2.2 信息素更新策略

在完成初始信息素分布的设定后，通过蚂蚁算法进行优化探索，构建一个包含m个候选解的筛选集合R。随后，为了增强路径间的区分度并促进算法的有效收敛，实施信息素浓度的更新策略。然而，传统的全局性更新方法难以在不同路径间创造出显著的信息素浓度差异，这会对后续优化进程产生障碍，并可能对算法的收敛速度产生影响。因此，本文将模拟退火机制中的Metropolis准则作为集合R中解的评估与筛选机制，生成新的优化解集Rnew并更新对应的信息素浓度［14］。设定筛选集中解的目标函数值为zi，依据特定接受准则

Pi=1，zilt;zopt

exp-zi-zoptkT，zi≥zopt（20）

判断当前解是否应被纳入优化解集Rnew之内，其中：zopt是当前最优值；参数k为一固定常数因子；T为实时温度，随着迭代次数的增加，T按照预设的衰减率逐渐降低。当zilt;zopt时，将所得解放入优化解集中，反之，随机生成一个数r，当rlt;exp-zi-zoptkT时，将解放入优化解集中。在高温阶段，T值显著提升，计算结果较大，此条件下，筛选机制更加宽松，导致更多潜在优质解被纳入更新后的优化解集Rnew中，这一策略有效缓解了算法可能遭遇的早熟与停滞的问题。相反，在低温阶段，T值相应减小，计算结果较小，此时，Rnew中优质解的纳入变得更为严格，优质解减少，进而加快算法收敛速度。

2.3 改进蚁群算法流程

改进蚁群算法求解本文优化模型的流程如图1所示。

3 实验仿真和数据分析

3.1 实验算例

选用Solomon题库中的R101算例作为验证算例，结合乌鲁木齐市30个社区菜店客户点实际信息数据进行仿真实验。30个随机分布的有一定需求量且具有时间窗约束的客户点被一个配送中心服务，所有配送车辆载重上限相同，设为100 kg，每辆配送车辆在客户点的服务时间都相同，并且服务时间设定为10 min。

3.2 算法参数设置

传统信息素蚁群算法：蚁群数量为50，迭代次数为50，信息素挥发因子为0.3，信息素浓度占比为1，可见度占比为0.25，此外，引入恒定常数100以调整路径评估的灵敏度。

改进信息素蚁群算法：将遗传算法部分的种群规模设定为100，迭代次数设定为5，选择操作算子设定为0.9，交叉操作算子设定为0.7，变异操作算子设定为0.05。在此基础上，蚁群规模固定为50只，迭代上限仍为50次，信息素挥发因子保持0.3不变。关键调整在于，保持信息素在决策中的绝对优势地位不变（占比仍为1.0），但可见度占比提升至2.5，常数依旧设定为100，此外，引入Boltzmann常数（取值为2）来模拟物理退火过程，温度衰减率设为0.9，初始温度设为30 ℃。

3.3 模型有效性验证

为了验证该模型的有效性，将传统VRPTW模型与本次研究的改进模型进行比较，选取30个社区蔬菜零售点的数据集作为测试案例，采用传统的蚁群算法对这两个模型进行优化对比。为确保实验结果的稳健性与可信度，每一组对比实验均重复执行5次，通过此方式有效规避了单次实验偶然性的影响，进而提升整体实验设计的科学性与有效性，取表现最优的结果作为最终的实验结果。具体测试结果如表1所列。

由表1可知，虽然使用改进模型进行路径规划时的传统优化目标相较于VRPTW模型的传统优化目标增加了0.3%，但是综合配送成本却降低了1.3%，通过对比可以得出，改进模型在降低综合配送成本方面有一定的优势，也验证了其在实际应用中的有效性与优越性。

3.4 基于遗传算法的信息素验证初始化成效

为验证改进蚁群算法（IP ACA）生成初始化信息素比传统蚁群算法（ACA）能够更加有效地改善蚁群算法在前期存在的信息素匮乏，收敛速度慢的问题，通过传统蚁群算法和本文改进蚁群算法对上述案例进行求解，对比结果如表2所列。表2中的平均配送成本和平均收敛次数都是每个算法进行10次运算所求得的平均值。

通过表2的对比分析可知，相比于传统信息素的蚁群算法，本文改进算法的平均收敛次数降低了36.8%，并且配送成本也有所降低。所以，使用本文改进的蚁群算法可以提高初始化信息素的蚁群算法的收敛速度，提高解的质量。

3.5 算法对比

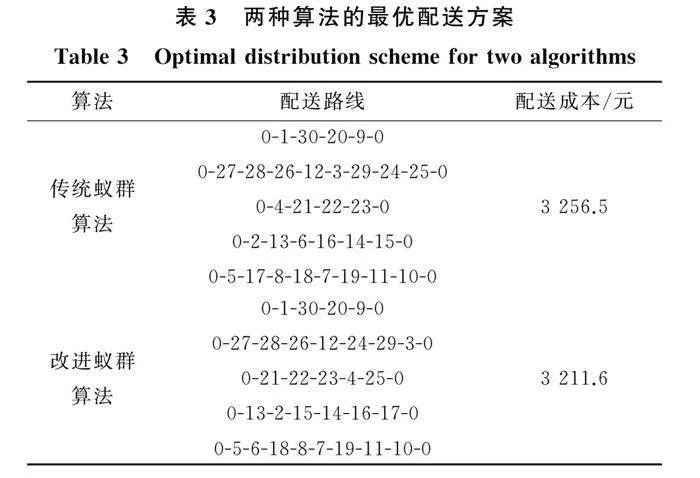
通过对比传统信息素蚁群算法和改进信息素蚁群算法的求解结果，验证该改进算法的有效性。在实验过程中分别以两种方法进行10次随机实验，选择最优实验结果为最终结果，两种算法的最优配送方案如表3所列。

从两种算法的配送方案可以看出，两种配送方案都具有5条配送路径，因此也需要5辆配送车辆，但是配送成本存在差异，传统蚁群算法的配送成本需要3 256.5元，而本文改进的蚁群算法的配送成本需要3 211.6元。最优解收敛曲线如图2所示。由图2可知，在迭代到20次时，IP ACA达到最优收敛效果，并且相较于ACA，其最终的目标函数值也更小，所以，改进蚁群算法合理有效，且优化模型求解质量更高。

4 结论

本文针对城市社区生鲜农产品配送成本高、耗能高、距离不优的现状，以综合配送成本最小化为目标，对生鲜农产品配送问题进行研究，得到以下成果：

（1） 构建优化模型。综合考虑了生鲜农产品配送过程中的配送费用、货损成本、客户时间窗约束的惩罚成本等构建了生鲜农产品配送路径优化模型，并通过与传统模型进行对比，验证了本文的优化模型可以降低综合配送成本。

（2） 算法优化。本文的遗传-模拟退火机制的改进蚁群算法比初始化信息素的蚁群算法具有更快的收敛速度，并且所求解的质量更高。

（3） 算法性能的比较。将本文所改进的蚁群算法与初始化信息素的蚁群算法进行比较，验证了本文改进算法可以有效降低综合配送成本，并且具有更高的收敛效率。

参考文献：

［1］YANG B.Machine learning-based evolution model and the simulation of a profit model of agricultural products logistics financing［J］.Neural Computing and Applications，2019（31）：4733-4759.

［2］FASANYA I O，ODUDU T F.Modeling return and volatility spillovers among food prices in nigeria［J］.Journal of Agriculture and Food Research，2020（2）：100029.

［3］ WANG Y M，YIN H L.Cost-optimization problem with a soft time window based on an improved fuzzy genetic algorithm for fresh food distribution［J］.Mathematical Problems in Engineering，2018：1-16.

［4］AGUSTINA D，LEE C K M，PIPLANI R.Vehicle scheduling and routing at a cross docking center for food supply chains［J］.International Journal of Production Economics，2014（152）：29-41.

［5］ 王敏荣.生鲜农产品配送路径优化研究［D］.合肥：合肥工业大学，2020.

［6］ 葛显龙，孔阳.带有时间窗的生鲜物流配送路径优化研究［J］.数学的实践与认识，2016，46（12）：78-87.

［7］ 赵志学，李夏苗，周鲜成，等.考虑交通拥堵的冷链物流城市配送的 GVRP 研究［J］.计算机工程与应用，2020，56（1）：224-231.

［8］ 范厚明，李荡，孔靓，等.模糊需求下时间依赖型车辆路径优化［J］.控制理论与应用，2020，37（5）：950-960.

［9］ 任腾，罗天羽，谷智华，等.考虑同时取送货的城市物流共同配送路径优化［J］.计算机集成制造系统，2022，28（11）：3523-3534.

［10］ 王玖河，安聪琢，郭田宇.时变路网下电动冷藏车配送路径优化研究［J］.工业工程，2022，25（4）：60-69，107.

［11］ 尹三平.生鲜农产品物流配送路径优化研究：以A公司为例［J］.物流科技，2019，42（2）：51-54.

［12］ 鲍惠芳，方杰，张进思，等.基于改进蚁群算法的低碳冷链配送路径优化［J］.系统仿真学报，2024，36（1）：183-194.

［13］ 康凯，韩杰，普玮，等.生鲜农产品冷链物流低碳配送路径优化研究［J］.计算机工程与应用，2019，55（2）：259-265.

［14］ HANINE M，BENLAHMAR E H.A Load-balancing approach using an improved simulated annealing algorithm［J］.Journal of Information Processing Systems，2020，16（1）：132-144.

Research on fresh distribution path optimization

based on improved ant colony algorithm

HE Wenlong，XU Hao，BI Deming，ZHANG Jinlong，LI Li

（School of Transportation and Logistic Engineering，Xinjiang Agricultural University，Urumqi 830052，China）

Abstract

Aiming at the unreasonable distribution cost in the distribution path optimization of fresh agricultural products，the distribution of fresh agricultural products in Urumqi community vegetable shop was taking as an example.According to the characteristics of high freshness requirements of fresh agricultural products and complex distribution situation，taking into account its transportation costs，goods loss costs and customer time window constraints，an optimization model targeting the minimization of comprehensive distribution cost，it proposes an improved ant colony algorithm of genetic-simulated annealing mechanism to optimize the distribution path of fresh agricultural products.Combining simulation experiments to verify the effectiveness of the model and improve the algorithm，this essay provides a theoretical basis for the optimization of the distribution path of fresh agricultural products in the community vegetable shops in Urumqi in the post-epidemic era.

Key words

Path optimization;Fresh agricultural products;Improve ant colony algorithm;Community vegetable shop

（本文责编：冯 婷）