标准量迷思概念的教学诊断

摘 要：学生在学习中普遍会产生迷思概念，针对比较量与标准量分率比较中出现的迷思概念，设计迷思概念的诊断工具、制造认知冲突活动、开展调整认知结构的教学活动，通过前后测的配对样本检测分析，发现臆测活动能产生认识冲突，学生能正确判断标准量，语言表征、图像表征、数字符号表征的转换和分母与标准量的关联，能有效促进学生理解比较量与标准量互相转换后分率的变化，更改迷思概念。

关键词：小学数学;标准量;迷思概念;教学诊断

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2024）31-0061-04

在教学中，面对经常出错的学生，教师尝试多种策略往往收效甚微，究其原因是学生对数学概念没有正确的认识。许多研究揭示，儿童在接受科学概念前，头脑中就存有许多解释世界的观念，也就是所谓的前科学概念或教学前概念。小学生在学习分数时，不仅在教学前有许多先有观念，在接受教学后，他们头脑中的概念与科学概念仍有差异。若学生的概念与科学概念不同，则被称为是错误概念或迷思概念。迷思概念有个体性、普遍性、动态性、牢固性、片面性的特征，只凭讲解很难改变。

分数是小学阶段重要的内容，是儿童将来学习许多数学概念和技能的基础和关键。因分数概念有部分整体、测量、商、比、算子五种形式的表达，所以学生在理解分数时，会出现很多迷思概念，如等分概念理念不足、理解“单位量”“标准量”有困难、受整数运算法则的影响等。笔者在学生解决分数问题中发现，学生存在标准量的迷思概念，本文以标准量的迷思概念为主线，尝试通过诊断、教学干预实现学生迷思概念的转变。

一、标准量迷思概念的诊断

学生在做判断题“5比4多，那么4比5少”时，绝大部分学生都认为是错的，是不是说明学生就不存在这样的迷思概念。笔者在对县区240名六年级学生（寒假刚到校）进行了测试：图书角有故事书70本，比科技书多，科技书有多少本？正确率是47.5%，分析学生的错误，学生用70×（1-）或70-70×来计算，这两种错误的思路一致，占全年级错误学生的75.0%，由此看到学生出现此类错误还是具有普遍性的。访谈出现此问题的学生，学生认为故事书比科技书多，那么科技书比故事书少，先用70×算出少的数量，再用故事书的数量减去少的数量就是科技书的数量。通过访谈可以看出学生对标准量的理解不到位，受整数比较负迁移的影响，形成了典型的关于标准量的迷思概念，即A比B多，B就比A少，这个迷思概念在判断题没有表现出来，而在解决问题时表现了出来，也反映出迷思概念的牢固性。标准量是指在表征一个数量时，至少需要另一个数量作为衡量的标准，我们把衡量物品所用的标准数量称为标准量，在实际教学中也有别的名称，如基准量，单位“1”，单位量等。下面设计迷思概念的诊断工具，方便诊断学生是否有此迷思概念。

可以通过不同的类型的测试题来检测，如填空题：男生比女生多 ，你认为女生比男生少（ ）。判断题：一件商品涨价，然后又降价了，这件商品的价格没有发生变化，你认为对吗？也可以看图（图1）填空：

女生比男生多;男生比女生少。

如果学生在不同类型的测试中，认为前后的分数要相等，则诊断学生具备这类迷思概念。

二、标准量迷思概念的干预

此迷思概念是由于分数比的意义的类化不足造成的，因个体不可能脱离两个量的关系来表征一个纯粹的“量”。如果学生不能理解每个分数所对应的标准量，就会对分数解决问题带来困难。如何改变学生的迷思概念？研究表明诊断教学理论可以有效改变学生的迷思概念，林福来教授将诊断教学理论具体化，把诊断教学分为三个环节：学生所犯迷思概念的诊断、针对学生的迷思概念制造认知冲突、调整学生认知的教学。依此设计以下诊断教学活动：

（一）诊断迷思概念

根据前面提到的诊断工具对学生进行测试，判断学生是否具有此迷思概念，将有此迷思概念的学生作为研究对象，进行教学干预。

（二）制造认知冲突

1.通过臆测制造认知冲突

（1）猜想：男生比女生多，你有什么猜想（女生比男生少）？

（2）举例制造认知冲突：让学生计算完成表1。

（3）观察表格并思考：如何通过数据来说明你的猜想是对的？

（4）尝试再举例计算，并比较前后女生的人数。

（5）想一想，按照同学们的猜想，为什么女生人数前后不相等，这是什么原因？

（三）调整学生认知的教学

1.理解标准量

（1）案例中认识标准量。

案例：如果你本次成绩是80分，你认为如何？

意图：一个数是无法比较好坏的，必须有另一个数做对比，另一个数就可以看成标准量。

（2）多案例中表达并归纳基本的表达方式，（比较量）比（标准量）多（少）……

2.铺垫原有知识

理解一个数比另一个数多几分之几，就必须理解一个数是另一个数几分之几的意义。这两个数也分两种情况，一种是兼容情况，另一种是不兼容的情况，设计以下教学活动帮助学生理解。

（1）兼容情况：观察图2，用分数表示男生与全班人数的关系并解释。

讨论交流：为什么是，而不是其他分数呢？

②不兼容情况：观察图3，用分数表示男生与女生的关系并解释。

讨论交流：男生是女生的几分之几？女生是男生的几分之几？两次用分数表达的为什么不一致？通过讨论认识到分母与标准量（或整体）相关联，分子与比较量（或部分）相关联。

3.多种表征转换促进理解

（1）图形表征到符号表征的转换

先出示4个圆和5个正方形，说一说圆比正方形少几分之几，展示不同的答案，并让学生讨论是还是，说明理由。

思考正方形比圆多几分之几？说明理由。为什么两次所用分数的分母都不相同？分子都相同？通过讨论认识到分母与标准量的份数相关联，分子与多（少）的份数相关联。

（2）符号表征到图形表征的转换

先出示两数关系，A比B多。让学生画图，比较分析不同的画法。思考根据什么确定A和B各是几份？因为分母是3，说明标准量B的份数为3份;分子为1，说明比较量A比标准量B多1份，即A为4份。

三、标准量迷思概念的改变

（一）前后测数据对比分析

通过以上的诊断教学干预，学生是否转变已有的迷思概念，理解分数中标准量的意义？根据表征理论，莱什和兰多认为是否理解的证据为感知、表征、联结、应用。联结就是表征之间建立联系。学生通过不同的表征转换，理解比较量与标准量的倍比关系。据此在设置测试题时以文字、图形、符号三种方式呈现。除了考虑不同的呈现方式，还从知识结构来分析两数分率比较。在测试题的命制上考虑两数分率比较的基本要素，分别为两数关系、标准量和比较量。命题检测试题框架如表2所示：

备注：1表示给定标准量的数量;2表示给定比较量的数量;3表示两量关系：A比B 多（少）几分之几;1^2表示已知标准量和比较量。

现举例说明，例1是已知标准量的数量和两数关系，求比较量。例2是已知一个数比另一个数多几分之几，找出哪个量是标准量。

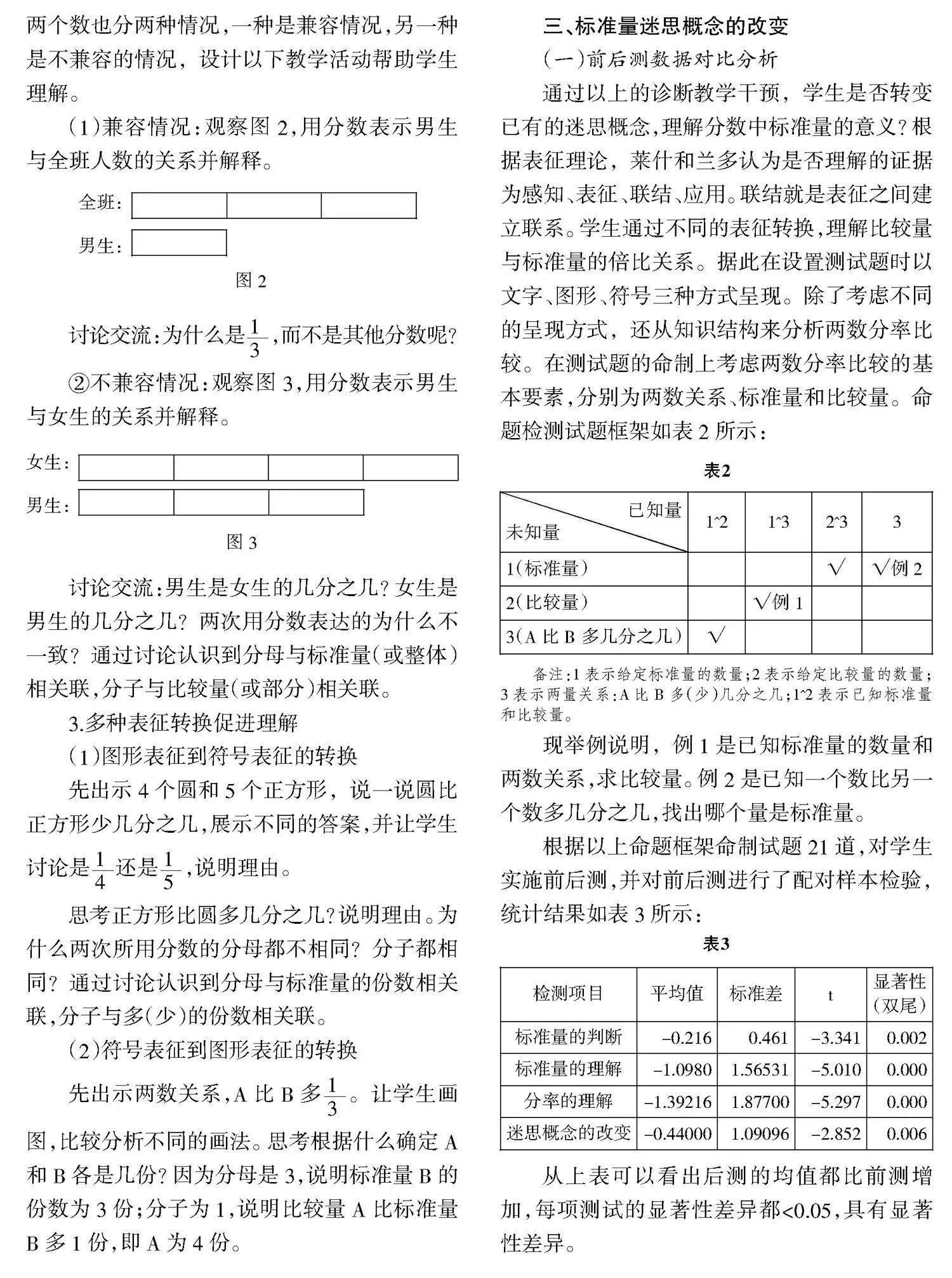
根据以上命题框架命制试题21道，对学生实施前后测，并对前后测进行了配对样本检验，统计结果如表3所示：

从上表可以看出后测的均值都比前测增加，每项测试的显著性差异都<0.05，具有显著性差异。

（二）表征转换促进学生两数比较分率的理解

基于研究对象对分数意义理解不深，教师以分数本身为切入口，让学生理解分母、分子分别表示的意义，再加上图形的直观辅助，学生对两数比较的分率就能正确理解。以下的两个教学片断就是以分母、分子为切入口，通过表征的转换促进学Xe8KxVlEWALlbEjl9pyZUw==生理解。

教学片断一：A比B多几分之几？

师：汽车是5辆，自行车是4辆，汽车比自行车多几分之几？

生：。

师：你认为多的理由是什么？

生：汽车是在自行车的标准上多的，自行车是4辆，所以多。

师：分母4是由谁来确定的，分子1是由谁来确定的？

生：分母是由标准量来确定，分子是看多了几份就是几。

教学中，笔者通过图让学生理解中分子分母所表示的意义，在检测中又让学生根据自行车比汽车少来画图，意图通过符号表征向图像表征的转换，强化了学生对分率的理解。

教学片断二：A比B少，B比A多几分之几？

师：老师有一个猜想，今年比去年少，去年就比今年多，对吗？为什么？

生：错的，因为标准量发生了变化，标准量变成了今年，今年和去年的不一样，今年是4份，去年是5份，所以去年比今年多。

生：标准量发生了变化，标准量决定分母，今年是标准量，今年是4份，所以分母是4，多了1份，所以是分子是1。去年比今年多。

以上教学内容是当标准量发生变化时，学生能否正确用分率表示两数关系。分析师生的对话，可以看出通过教学干预后，学生能抓住问题的关键，分母所表示的份数就是标准量的份数，不管怎么变，先看标准量是哪个量，确定标准量是几份也就确定了分母就是几，分子就是多或少的份数。

研究结果显示：通过对标准量的诊断教学干预，学生能正确判断标准量，对比较量与标准量比较的表达方式有正确的了解;通过学生的臆测活动后，学生对A比B多那么B就比A少的迷思概念能产生认识冲突;从分数的比的意义角度思考，通过语言表征、图像表征、数字符号表征的转换，以分母、分子的意义分析为突破口，学生能很好理解比较量与标准量互相转换后分率的变化。本研究的问题来源于学生解决问题中的迷思，具有一定的普遍性。教师可依据此例，针对学生学习中出现的其他的迷思概念，设计教学诊断工具进行教学干预，改变学生学习的迷思概念。

参考文献：

[1]杨伊生，刘儒德. 儿童分数概念发展研究综述[J]. 内蒙古师范大学学报（教育科学版），2008，（06）：130～134.

[2]鲍建生，周 超. 数学学习的心理基础与过程[M]. 上海：上海教育出版社，2009.

[3]辛自强，张 睆. 儿童的分数概念理解的结构及其测量[J]. 心理研究，2012，5（01）：13～20.