基于PBL模式的初中二次函数教学设计研究

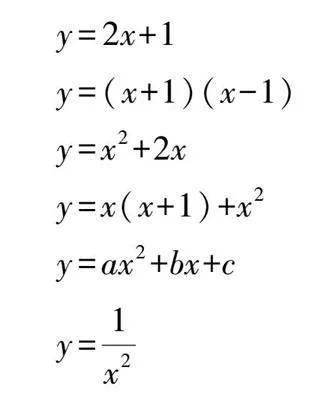
摘 要：基于问题的学习（PBL）方法聚焦于提升学生的自主思考和合作能力，通过解决问题以强化综合素质，符合新课程改革目标，是教育领域热议的话题。PBL注重学生的主体性和参与度，通过解决问题驱动，挖掘他们的实践力和创新精神。在初中数学教材中，二次函数起到了尤为关键的作用，其概念能有效关联现实生活，深入研究二次函数教学至关重要，因此文章基于PBL模式的初中二次函数教学设计展开研究。

关键词：初中数学；问题驱动；二次函数；教学设计

中图分类号：G633.6 文献标识码：A 文章编号：1673-8918（2024）44-0094-03

一、 基于初中数学新课改的要求

《义务教育数学课程标准（2022年版）》聚焦于教育导向的强化，致力于全面发展学生的综合素质，包括形成正确的价值观念、塑造必需的品性特质与关键能力，契合义务教育的培养要求。数学课程的教学目标聚焦于传授适应现代社会的知识、技能、思维模式和实践经验，同时激励学生对数学学习的热爱，增强他们的独立思考与团队协作能力，以及促进实践操作能力和创新精神的培养，从而构筑坚实的素养基础。顺应这一需求，基于问题的学习（PBL）模式被证明为有效的教学策略。PBL注重学生的主体性和参与度，通过解决问题驱动，挖掘他们的实践力和创新精神。此外，它倡导同伴间的合作交流，共同构建认知框架，有益于培养独立思考和团队协作的精神。

二、 初中二次函数教学存在的问题

首先，部分学生函数知识薄弱，难以领悟二次函数的概念、图像和性质，这在长远学习过程中可能形成障碍，阻碍他们深化对二次函数的理解。

其次，一些学生可能存在二次函数实际应用的理解局限。他们未能领会其概念在现实情境中的实用意义，缺乏将理论知识转化为解决实际问题的能力。这种理解不足往往会在后续学习中困扰他们，使其在应对现实生活中的问题时遭遇挑战，难以认识到二次函数的实际生活价值。同时，教师可能过于侧重理论知识的讲解，忽视了培养学生的实践操作能力和创新思维，这可能导致他们在实际应用中显得僵化和缺乏创新。

综上所述，对初中阶段的二次函数教学，关键在于强化学生对基础知识的理解与掌握，强调其在实际问题中的运用理解及解决问题的能力，并且倡导教师运用多元化的教学策略，以提升学生的学习成效和实践操作能力。

三、 基于PBL模式的初中二次函数教学设计研究

在教学过程中，我们着重于构建问题驱动的学习环境，激发学生思考，通过自主探索和集体讨论来领悟二次函数的内涵与外延。在实践环节，我们鼓励学生主动尝试，教师则依据他们的常见错误提供个性化指导。课堂中注重培养学生的主体性和对知识的深层次理解，特别是针对初中二次函数教学，我们将理解和运用二次函数概念作为核心，难点在于从实际问题中推导出解析式。

（一）创设情境，引入新课

教师引导：首先，让我们复习一下，同学们，你们还记得我们之前探讨的一次函数吗？能主动分享其定义的同学请举手，比如刚才那位可以清晰阐述的同学，显然他对此理解得比较透彻。无疑，大家都熟知一次函数的基础知识，然而其普适性如何呢？本课将详尽探讨这一问题。

1. 教师引导

教师通过提出问题导入，引导大家观察屏幕上的题目。

2. 情境创设

在课堂上，教师构建问题情境，带领学生探索：屏幕上展示的矩形花圃。

3. 问题设定

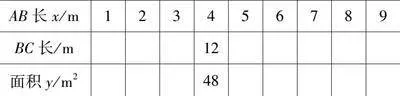
周长32米的花圃，AB和BC边已知，我们设AB为x米，目标是计算面积y。

4. 实践操作

要求学生将答案填写在表格中，加深对面积概念的理解与应用。

AB长x/m123456789

BC长/m12

面积y/m248

5. 深入探究

此步骤旨在促进同学们对这一概念的进一步研究与分析。

探讨一下，x的选取范围是否存在约束，是否能通过函数形式刻画y与x的关系？任务要求：让学生自行独立思考，然后表述出y关于x的函数表达式。

在实施中，教师设计源自实际生活的教学情境，通过构建相关的二次函数议题，激励学生自主推导二次函数表达式。然而，对学生来说，这个主题新颖且富有挑战性，他们可能会对新的函数形式产生疑惑。这种认知挑战恰好能刺激他们对学习的态度，推动他们探究和理解二次函数的实质。

（二）小组合作，探究问题

在授课环节，教师通过实例展示激发学生，以问答互动探寻函数关联。其设问聚焦于：“屏幕上这些函数表达式具有哪些共同特征？”接着，教师安排小组活动，明确要求学生在讨论中记录集体研讨的成果。

在教学课堂上，通过小组合作探讨解析式的共性。学生需分析并记录观察结果，发现特征：①单一未知数；②未知数的最高次数为2。小组合作有助于深化新函数理解，提升沟通与团队协作能力。分配特定解析式后，小组需研究图像性质（对称性、顶点、交点），并通过计算或绘图验证。讨论中，学生分享发现，教师引导，强调概念应用。活动旨在结合实际强化理论掌握，最终汇总各组成果，深化二次函数理解。

教学实践中，教师根据以上活动发起提问：基于前一议题的研讨，同学们能否为这些新兴函数命名并阐明理由？学生在研究过程中，应依据函数特性及普适性赋予名称，如他们会将这类函数统称为“二次函数”，鉴于所有函数中未知数的最高次数均为2。教师可以通过对比二次函数与一次函数的差异，引导学生尝试给二次函数命名。大部分学生能识别出这种新函数与一次函数的不同，从而冠以“二次函数”之名，有部分学生可能源于对函数特性深层次的理解，或受章节标题影响而命名。

（三）分析条件，解构问题

完成问题陈述后，教师需激发各学习小组进行深入研讨。研讨初期，多数学生能独立整理问题求解策略，继而轮流呈现个人的研究结果。学生对分享环节中多元的探究路径展现出强烈的求知欲，并积极地剖析，提供相应的“论据”以佐证其见解。通过集体探讨，多数小组最终能形成共识，共同制订最优解决方案。

在教学研讨环节，教师需深入各小组，聆听学生的表达并解决学生的困惑，运用提问作为引导工具，推进问题逐步解决，促使探究深化。实践中，教师应激发学生在特定情境下分析问题的能力，例如：能否从一次函数的基本定义出发，独立提炼出二次函数的特性？教师应组织学生进行小组深度探讨，充分利用教材资源，以深化他们对二次函数本质及其性质的进一步理解。学生需重温一次函数的特征，然后对比其与二次函数的区别，以此为基础构建对二次函数的理解。在小组合作中，学生积极参与，通过互动交流，培养探究、发现和概括的能力。最终，教师的总结讲解将巩固学生对二次函数概念的掌握，确保他们准确理解这一核心知识点。

例如，通过学生参与实践操作，判断以下哪些函数属于二次函数。

y=2x+1

y=（x+1）（x-1）

y=x2+2x

y=x（x+1）+x2

y=ax2+bx+c

y=1x2

在小组协作的互动中，学生针对有争议的函数表达式展开了讨论，借此巩固对二次函数的理解。在这6个表达式中，二次函数特指第二个和第三个。教学过程中，教师促使学生通过比较一次函数与二次函数的异同，加深他们对二次函数概念和性质的理解，并激励他们用自己的语言描述二次函数的定义。课堂中融入了小组讨论与展示活动，旨在增强团队协作与沟通能力，借此机会检验学生对二次函数概念的掌握和理解。此外，课堂上设置了小组讨论与展示环节，学生得以分享和质疑彼此对二次函数概念的理解。这种活动促使学生理解二次函数的内涵与外延，同时明确认识到一般式中各项系数和常数项的具体含义及其作用。这样的教学设计有助于教师传授二次函数的概念，培养学生的合作精神与探究能力，从而提升教学的有效性。

（四）动手操作，解决问题

动手操作让学生解决问题是PBL教学法的关键步骤之一。在课堂上，通过分组活动促进团队合作：每个成员独立构建一个二次函数，并要求小组成员解析其二次项系数、一次项系数和常数项。

例如：某花园为300m×90m矩形，在其中修建宽度相等的十字道路，设道路宽度为x米，种花的面积为y平方米。能否通过已学知识，推导出种花的面积y关于道路宽x的函数关系？同时，确定道路宽度的适宜范围。

该教学设计促使学生通过探究构建二次函数模型，实施阶段，教师可带领他们到校园参观花坛，从学校内的花坛问题出发，以小组合作形式合作并解决，彰显了PBL教学法中项目驱动的学习方式。解决过程中，学生可能需运用一元二次方程或二次函数的性质，加深理解方程、不等式与二次函数的关联。这种思考和探索活动有效地锻炼了学生的数学思维能力，课堂的多元性激发了他们进一步探索二次函数的兴趣和求知欲望。

四、 归纳总结，建立联系

数学教学中采用PBL模式的目标超越了简单的实际问题解决，它旨在促使学生深入理解问题核心，构建数学模型，并能在新情境中有效应用。要达成这个目标，教师关键在于引导学生在问题解决过程和后续阶段，进行系统的指导、归纳与总结，提炼所用的数学知识、技能和思维方式。

在二次函数教学环节中，教师可设计问题情境，引发学生思考：“面对此难题，我们的处理流程如何？解决问题的核心何在？”通过这些问题的驱动，学生将复盘求解极值问题的全程，归纳并提炼出求解策略和具体步骤。教学中，倡导教师采用思维导图的形式，以可视化的系统结构展现问题解决策略与途径。电子白板的数学功能被教师有效利用，可现场绘制思维导图，详尽演示求解二次函数极值问题的流程，以此增强学生对概念的领悟。

五、 结论

PBL教学法在初中数学教学中的应用能激发学生参与问题解决的积极性，实现自我导向学习，他们能运用所学知识与技能，通过小组合作来解决问题，从而培养数学抽象思维和问题解决能力，进而提升学习的有效性。同时，教师需适应这种模式，不断加以改进，及时更新传统教学理念，提升问题设计和课堂掌控的能力。鉴于PBL方法的实际效果，它应被视为提升数学教学质量的有力“工具”，以促进教学质量的实质性提升。

参考文献：

［1］冯加辉.核心素养下高中数学PBL教学模式的分析与实践应用研究［J］.高考，2024（8）：88-90.

［2］邹源明.基于PBL教学模式的高中数学教学策略研究［J］.名师在线，2024（5）：32-34.

［3］刘婷婷，黄金莹.PBL教学模式在高中数学教学中的应用探究［J］.求知导刊，2023（34）：92-94，106.

［4］马颢.PBL教学模式深化高中数学课堂——以“等比数列”单元为例［J］.新课程，2023（25）：34-36.

课题信息：广州市教育科学规划2022年度课题“‘双减’背景下‘三位一体’初中数学小组分层合作教育模式教学成果的实践研究及推广”（课题编号：202213956）；2021年广州市教学成果培育项目“‘三层六人三位一体’——初中数学小组分层合作教育模式构建与实践创新”（课题编号：2020123168）。

作者简介：黄宁波（1980～），男，汉族，广东兴宁人，广东省广州市番禺区育龙中学，研究方向：中小学数学教学。