基于改进bi-kmeans算法的学生消费水平分析

摘 要：以高校校园内学生的移动支付消费记录为基础数据，利用bi-means聚类算法对其处理并进行分析，挖掘出这些学生消费水平背后的隐藏信息。通过改进欧式距离、k-means和bi-kmeans，应用于清洗过后的消费记录，划分出不同层次的学生消费群体，以散点图的直观方式呈现。实践表明，改进后的bi-means算法结果的划分更合理，可向学校资助部门提供参考。

关键词：bi-kmeans；消费水平；聚类算法；数据挖掘；欧式距离

中图分类号：TP 312 " " " " 文献标志码：A

高校学生采用现代移动支付的方法，在校内的消费行为都会留下详细记录。从这些详细的记录中分析每个学生的消费水平。本文在传统bi-kmeans聚类算法和传统欧式距离的基础上，提出改进方法，应用于学生消费水平分析，得出结论，并与传统聚类方法的结论进行比较。

1 研究现状

1.1 k-means聚类算法

1976年，MacQueen基于前人的研究提出了k-means聚类算法。其中心思想为给定数据集划分为k个簇，每个簇的质心由全部点的中心来决定。中心是簇中全部点的平均值，称为k均值，k个初始值由用户指定。k-means聚类算法的优点为原理简单、易于实现并且接近线性的时间复杂度。缺点为对k值的设置依赖性较高，还可能限于局部最优。

1.2 bi-kmeans聚类算法

bi-kmeans的基本思想与k-means一致，区别在于k值是从1开始迭代，逐步递增，直到达到期望值为止。在每次递增的过程中，选择可以最大程度地降低平方和误差SSE的簇，将其一分为二，不断重复。

因为不需要给定k个初始质心，所以可以避免给定初始质心的不合理性。k值是从1缓慢增长到预期值，在每次迭代的过程中，新的质心和新的簇都是从被分裂簇一分为二产生的。这样类似细胞一分二的最简单分裂，不会存在其他分裂方案。

1.3 国内研究

应用范围最广的k-means聚类算法已经广泛适用于数据挖掘任务中。一卡通系统已经在全国高校大范围推广，该系统专用于收集高校学生这个特定人群的详细消费记录，已经有多人尝试用k-means结合一卡通的模式进行数据挖掘。龚黎旰等[1]以校园一卡通消费记录为数据基础，利用大数据和数据挖掘技术对其进行分析。柴政等[2]利用数据挖掘方法中的神经网络分析校园一卡通消费记录，从客观的角度评判学生的贫困程度及精准地划分贫困群体。

2 改进算法

bi-kmeans算法来源于k-means算法，而k-means算法又基于欧式距离。传统的3个算法不能简单套用，须根据实际环境进行改进。

2.1 改进欧式距离

欧式距离全称为欧几里得距离，其中心思想为以向量为基准，衡量多维空间中任意两点间的绝对距离，即两点之间的最短直线距离，如公式（1）所示。

（1）

式中：x 、y 为多维空间中的任意两点；xi和yi分别为两点各自的各向量； d（x，y）为欧式距离。

当衡量真实的多维空间中的两点距离时，欧式距离非常有效。当应用于抽象概念的空间中两点距离时，欧式距离会暴露出一定的弊端。当其中某些向量显著大于其他向量甚至差距大到数量级差异时，欧式距离的结果不再是由各向量共同决定的。其决定因素只由数量级最大的向量构成，次数量级向量和小数量级向量的影响因子大幅度缩小，几乎不起作用。

令各向量回归到同一个数量级别即可避免这个弊端，比较有效且简洁的解决办法是缩小较大向量的数量级或增加较小向量的数量级。因为这样可以从源头减少整个算法过程的计算量，所以缩小较大向量的数量级更有效，在欧式距离中为各向量增加权重，称为加权欧式距离，如公式（2）所示。

（2）

式中：wi为各向量的权重，其余标识与公式（1）完全一致。

2.2 改进k-means

k-means也称为k均值，其是最简单的聚类算法，具有通俗易懂、易于实现的优点。其工作原理如下。

步骤一：确定k个初始点作为初始质心。这k个初始质心不必要求为数据集的真实点，可以是数据集范围内的任意点。确定方法可以是随机，也可以是人工。步骤二： 根据现有的质心集，将数据集中每个点分配到1个合适的簇里。其方法是计算每个点与每个质心的距离，为每个点找到距离最近的质心，即可分配到该质心对应的簇里。步骤三：分配完成后，重新确定每个簇里的质心，即该簇的质心更新为该簇里全部点的平均值。步骤四：重复步骤二、步骤三，直到质心集停止更新为止。此时，数据集中的全部点与对应的质心距离都为最近。上述流程可以满足大多数普通场景的要求，但是当聚类结果以图形等方式展现时，质心集会变得杂乱无章。此时，需要在运算过程中加入排序标准，使质心集依序排列，同时各簇也需要相应调整顺序，称作有序k-means。具体伪代码如下。

随机创建k个数据集范围内的点并排序，作为初始质心。

While任意数据点改变簇分配结果

｛ for遍历数据集里的每个数据点

｛ for遍历每个质心

｛ 计算当前数据点与当前质心的加权欧式距离

｝

依据最近原则，重新分配每个点到新簇

｝

for遍历每个簇

依据当前簇里的全部点，更新当前质心

｝

2.3 改进bi-kmeans

bi-kmeans的思想建立在传统k-means的基础上，每次只做二分化解，直到满足指定簇数目为止。其步骤有以下2个。首先，将全部数据点视为一个簇，将当前簇一分为二。其次，选择其中一个簇再一分为二，选择的标准是划分该簇以最大程度地减少平方和误差SSE的值。重复这个划分过程，直到簇的数目达到k为止。当传统的bi-kmeans算法每次一分为二时，都是在质心序列尾部附加新质心。当输出方式有图形要求时，也会面临与k-means一样的问题。改进算法是在每次划分的过程中根据质心的排序标准，将新质心插入质心序列中，称作有序bi-kmeans。伪代码如下。

全部点视作一个簇，即原始簇

while簇的数目lt;k

｛ for遍历每个簇

｛ 调用有序k-means，计算当前簇二分后的总误差

找到目标簇，并保留二分后的结果

｝

在目标簇对应的目标质点后插入一个位置，将目标质点及后面一个位置更新为二分后的两个质点

目标簇划分为两个新簇

｝

3 分析过程

3.1 数据来源

某高校采用现阶段流行的移动支付方式，校园内部遍布移动支付终端。消费者可以灵活选择支付方式，包括现金支付和移动支付。由于移动支付具有便利性，几乎无人选择传统的现金支付。就餐环境已经彻底抛弃现金支付，完全采用移动支付。

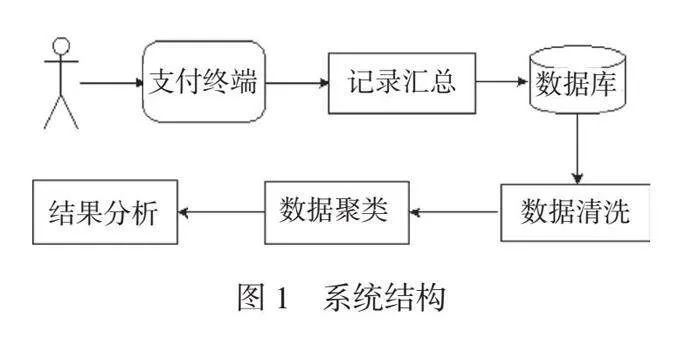
当每天学生在消费时，与支付终端的交互记录源源不断汇总到后台服务器上，形成详细的交易数据库。在这个消费数据库中，包括有时间、地点以及窗口等信息。通过对这些记录进行数据挖掘，可以得到预期的聚类结果，可以分析出学生的消费习惯、消费水平等潜在信息。消费系统的结构如图1所示。

3.2 实践设计

全体学生消费记录按照时间段为标准，选取该时间段内的记录作为样本，每个学生是一个数据点p，总共有n个学生，这些样本全体组成数据集P，有pi∈P，i∈[1，n]。传统的k-means算法需要给出2个初始参数：初始质心集Ce和聚类数目k。质心集Ce中有k个质心ce，即cej∈Ce，j∈[1，k]。

根据质心集Ce划分出来的簇Cl，有CljP，j∈[1，k]。Clj的长度为nj，有nj∈[1，n]，j∈[1，k]。在迭代的过程中，Ce和Cl都处于动态的状态。划分簇Cl的标准为加权欧式距离，如公式（2）所示，即簇中每个数据点p到相应质心ce的距离为最近。

3.3 数据格式

全部的消费记录是直接进入数据库，以最原始的格式存储（如图1所示）。其优点是保留了数据最初始的状态，各项目可以根据自身的需求提取和处理原始数据。同时，缺点在于数据的原始格式不能完全满足各项目的特定要求。因此要经历数据的清洗阶段，包括数据筛选、数据集成、类型转换和数据归约，然后才能进行数据的聚类。数据清洗后的格式见表1。表中为有效字段，无效字段已省略。

3.4 实践流程

根据上述的数据来源、数据格式和实践设计，整个实践过程分为实践有序k-means和实践有序bi-kmeans。

3.4.1 实践有序k-means

步骤一：利用质心随机函数，在数据集P范围内随机生成k个质心ce，有公式（3）成立。生成后对全部质心ce排序，组成质心集Ce。

cej≤max（P） " " " " " " " " " " " " " （3）

式中：max（P）为数据集P的范围，即数据集P各向量的最大值。

步骤二：对于每个点p来说，利用加权欧式距离公式（2），找到与之匹配的距离最近质心ce，如公式（4）所示。

min（d（pi，ce））=d（pi，cej）lt;d（pi，cel） " " " " （4）

式中：d（pi，ce）为数据点pi与质心ce间的距离；d（pi，cej）为数据点pi与质心cej间的距离；d（pi，cel）为数据点pi与质心cel间的距离，j，l∈[1，k]，并且j≠l。质心cej是距离点pi最近的质心；cel是非cej的其他任意质心。该步骤更新了每个簇的划分，即更新每个簇里的点成员。

步骤三：每个簇更新后，更新簇里的质心，如公式（5）所示。

（5）

式中：nj为当前簇的长度，有j∈[1，k]，nj∈[1，n]。

步骤四：由于在步骤三中每个簇Clj都产生新的质心cej，为验证当前质心集是否稳定，因此重复步骤二、步骤三，直到每个簇划分停止更新。当前循环步骤二、步骤三的结果与上一次循环的结果一致。

3.4.2 实践有序bi-kmeans

步骤一： 数据集P里的全部点p作为第一个簇的成员，此时Cl1=P，Clj=ϕ，j∈[2，k]。质心集的长度为1，这个质心ce1为全部点的平均值，如公式（4）所示。此时，j=k=1，n1=n。

步骤二：对于每个不为空的簇调用有序k-means，进行二分计算，即调用时设定有序k-means的k=2。能参与二分计算的簇有Cli⸦P，Cli≠ϕ，i∈[1，k]。找到二分后可以令数据集P总距离最小的簇Cla，a∈[1，k]，如公式（6）所示。

（6）

式中：d（P，Ce）为数据集P到各质心的总距离；∑d（Cl，ce）为每个簇Cl到与其匹配质心ce的距离总和；d（Cla1，cea1）和d（Cla2，cea2）为簇Cla二分后的2个簇内距离；d（Clb1，ceb1）和d（Clb2，ceb2）为簇Clb二分后的2个簇内距离，此时a≠b，Cla≠Clb，即Clb为非Cla的其他任意簇。

步骤三： 更新质心集Ce，将cea替换为cea1，并在其后插入cea2。cea1和cea2的获取方式如公式（5）所示。此时，j=a。

步骤四： 当质心集Ce的长度小于k时，回到步骤2进行重复迭代。当质心集Ce的长度等于k时，划分停止。此时，已经达到二分后k个质心、k个簇的要求。

4 实践结果

每个学生每天消费3次，则总消费记录数量应该大于学生总人数的3倍。预期的情况是学生有可能每天消费次数超过3次，同时还会有非学生的消费记录。但是实际情况是总消费记录数量远小于学生总人数的3倍。因为学生可选的就餐地点众多，不会局限于只在校内消费，所以结果是很多学生在某些时间点的消费记录为空白。本次选取样本的时间段为2021—2022年，即2021年9月1日—2022年8月31日。学生样本人数超过6000人，每个学生整个学年的消费次数和消费金额进入样本库，记为1个点。经过初步筛选后，已经剔除极其孤立的5个点。本次实践环境为Intel Xeon CPU E7-8880 v4 @ 2.20GHz，VMware ESXi 6.0.0，CentOS7.9.2009，Django4.1.7，mysql8.0.31，Nginx1.22.1，Plotly5.13.1。

4.1 k-means结果

不论是传统k-means，还是有序k-means，都需要事先提供k个初始质心。确定k个初始质心的方法可以是随机方式，也可以是人工方式或者人工干预下的随机方式。确定方法的选择对分配结果的影响不大，当多次计算后会发现结果趋近一致，而对于运算的迭代次数影响很大。k值的大小是一个经验判断的结果，可以从1～n中任意选择，根据项目的基本需求来确定。学生的消费能力是学生家庭生活水平的重要标准，通常校内的贫困比例为1∶5，因此，本次k值确定为k=5。传统k-means结合传统欧式距离聚类的结果如图2所示。有序k-means结合传统欧式距离聚类的结果如图3所示。

图2中各质心与原点的距离由近及远依次为质心4 lt; 质心3 lt; 质心2 lt; 质心1 lt; 质心0，相应的簇顺序为簇4、簇3、簇2、簇1和簇0。质心和簇这样的乱序排列对图片呈现结果的影响几乎可以忽略，缺点是当需要顺序分析时无法满足要求。

有序k-means在迭代过程中，对质心成员排序。因此，在图3中各质心到原点的距离呈现出自然数顺序，各簇也相应为自然数顺序。这样的排序利于在后续研究中顺畅使用。从图2和图3可以看出，各簇之间出现了严格的水平分界。其原因是各点的2个向量之间存在不同数量级别的差异。当计算传统欧式距离时，消费金额比消费次数高1个数量级，消费金额的作用因子较大，消费次数的作用因子较小，因此各点的消费金额成为传统欧式距离的主要影响因素，消费次数则成为可有可无的因素。

4.2 bi-kmeans结果

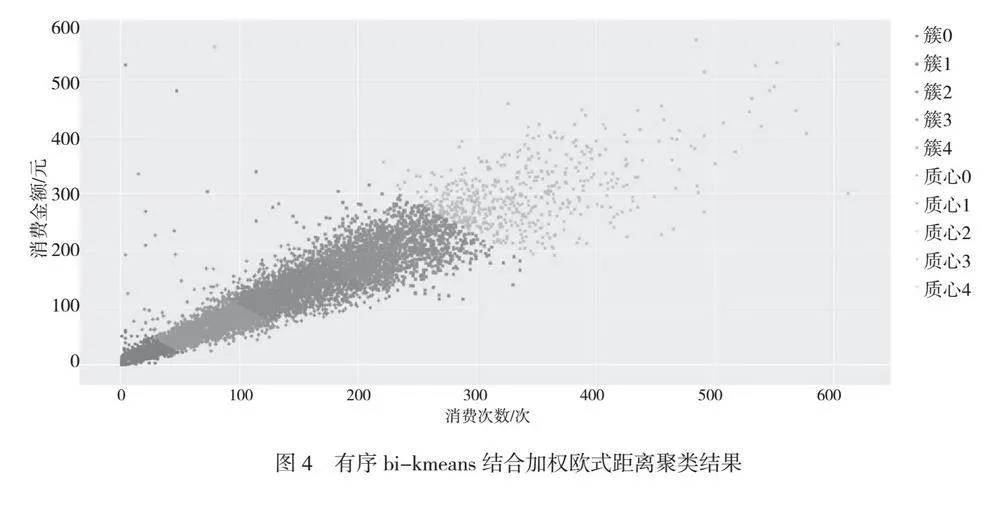
按照一致性原则，bi-kmeans的k值也确定为k=5。由于bi-kmeans的k值在迭代过程中是从1逐步增加的，并且每个质心都是由簇内点共同决定的，因此不需要在迭代之初设定初始质心。有序bi-kmeans结合加权欧式距离聚类结果如图4所示。

由于消费金额比消费次数高1个数量级别，因此在加权欧式距离中消费金额向量的权重设定为1/10，消费次数的权重设定为1。从图4可以看出，划分簇边界的决定因素不再由消费金额单独决定，而是由消费金额和消费次数共同决定，2个决定因素的因子比例为1∶1，簇边界的划分由2个向量来共同决定。

簇cluster3与簇cluster4之间的边界从图3到图4变化，代表有部分学生消费金额不高，因此在图3中被划为簇cluster3，采用加权欧式距离后这部分学生被划入簇cluster4。显然，这部分学生是高消费次数、低消费金额，更符合家庭贫困的要求。设定k=5的初衷在于寻找真实的贫困学生，采用有序bi-kmeans结合加权欧式距离的聚类方式是更优算法。

5 结语

高校学生在校园内部的消费行为通过移动支付，都会留下痕迹。本例采集全样本，通过筛选、集成和转换等系列操作后，提出有序bi-kmeans结合加权欧式距离的方式来得出聚类结果。根据聚类结果对比，得出结论为有序bi-kmeans结合加权欧式距离的算法为更优算法，可以避免传统算法的弊端，可以找到目标学生群。优化后的聚类算法更客观地通过学生消费行为反应出学生的消费水平，为关心学生生活的部门提供更准确的分析结果，解决人为划分目标学生群效率低、主观因素过重等缺点。本例中的样本分布比较均匀，2个向量基本为正比关系且样本量足够大。当实践k-means算法时，并未出现局部最优和空簇的情况。在实践过程中，当人为缩小样本量到足够小时，暴露了k-means算法的缺点。改进后的bi-means算法当样本量大和小时都表现得比较优秀。

参考文献

[1]龚黎旰，顾坤，明心铭，等.基于校园一卡通大数据的高校学生消费行为分析[J].深圳大学学报理工版，2022，37（增刊1）：150-154.

[2]柴政，屈莉莉，彭贵宾.高校贫困生精准资助的神经网络模型[J].数学的实践与认识，2018，48（16）：85-91.