基于协同优化算法的供应链网络设计与管理研究

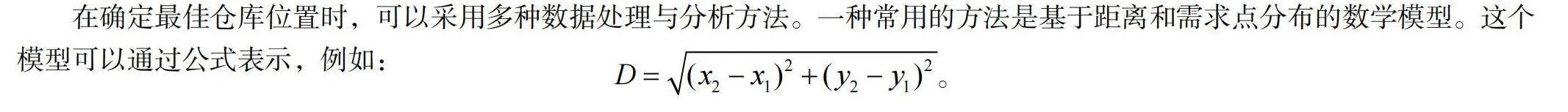
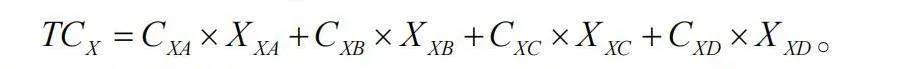
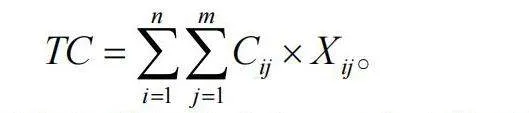
摘 要：文章探讨了基于协同优化算法的供应链网络设计与管理问题的解决方案。传统供应链网络设计面临路径规划、物流选址等挑战，文章在对这些问题进行深入分析的基础上，详细介绍了协同优化算法的基本原理，探讨了其在供应链管理中的潜在应用，提出了基于协同优化算法的供应链网络设计与管理模型，并详细描述了模型的构建过程和优化目标。通过仿真实验验证了协同优化算法在实际应用中的有效性和可行性，结果表明，该算法能够有效解决现实世界中的供应链管理问题，为提高供应链效率和降低成本提供有效的解决途径。

关键词：供应链网络设计；协同优化算法；物流选址；路径规划

中图分类号：F259.22 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.028

Abstract： This paper explores solutions to the problems of supply chain network design and management based on the collaborative optimization algorithm. Traditional supply chain network design faces challenges such as route planning and logistics site selection. Based on the thoroughly analysis of above challenges， this paper provides a detailed introduction to the basic principles of the collaborative optimization algorithm and discuss its potential application in supply chain management. A supply chain network design and management model based on the collaborative optimization algorithm is proposed， along with a detailed description of the model's construction process and optimization objectives. The effectiveness and feasibility of the collaborative optimization algorithm in practical applications are verified through simulation experiments. The results indicate that the algorithm can effectively address supply chain management problems in the real world， and provide an effective approach to improving supply chain efficiency and reducing costs.

Key words： supply chain network design; collaborative optimization algorithm; logistics site selection; path planning

收稿日期：2024-05-23

作者简介：郭福利（1981—），男，河南商丘人，华北水利水电大学，副教授，博士，研究方向：物流与供应链管理。

引文格式：郭福利，高燚．基于协同优化算法的供应链网络设计与管理研究[J]．物流科技，2024，47（22）：111-114.

0 引 言

随着全球经济的发展和市场竞争的加剧，供应链网络设计与管理成为了企业经营所面临的重要问题，传统的供应链网络设计往往存在路径规划不合理、物流选址不科学等问题，导致物流成本高、运输效率低，为解决这些问题，需要引入先进的优化算法，以提高供应链网络设计的效率和管理水平。

1 路径规划优化

传统的路径规划方法往往只考虑最短路径或最快路径，却忽略了供应链网络中其他重要因素的影响，基于协同优化算法的路径规划模型能够综合考虑货物流通量、运输成本、交通拥堵等因素，打造全局最优的路径规划方案，在进行路径规划优化前，要收集相关数据并进行数据分析，以建立合适的路径规划模型[1]。

1.1 节点信息分析

给定的供应链网络中，包括生产地（节点A）、销售地（节点B）和中转站（节点C、D、E），每个节点之间的距离和运输成本是决定路径选择的重要因素。这些信息对于设计最优路径规划方案至关重要。表1展示了不同节点之间的距离和运输成本数据。

在表1中，数字表示对应节点之间的距离（假设以千米为单位），例如，从节点A到节点B的距离为30千米。

为了计算最优路径，可以使用最短路径算法，如Dijkstra算法。该算法可以基于节点之间的距离信息，计算出从一个节点到另一个节点的最短路径。其基本思想是从起始节点开始，逐步扩展到其他节点，直到找到目标节点。在这个过程中，通过比较不同路径的长度来确定最短路径，除了距离信息，运输成本也是路径规划的重要考虑因素之一，假设每千米的运输成本为1货币单位，那么可以通过货币单位乘以距离来计算节点之间的运输成本，例如，从节点A到节点B的运输成本为30货币单位。

1.2 货物流通量分析

在这一案例中，公司每天需要将1 000个产品从生产地运送到销售地，同时，考虑到不同中转站的容量限制，货物流通量数据已成为一个重要指标，表2展示了各个中转站的容量限制和每日运输量。

容量限制表示每个中转站能够容纳的最大货物数量，而每日运输量则表示每天通过该中转站的实际货物数量，为了更好地理解货物流通量的影响，可以使用以下公式计算各中转站的利用率：

利用率 = （每日运输量 / 容量限制） * 100%。

例如，对于中转站C，利用率为：

利用率 = （300 / 500） * 100% = 60%。

通过这样的计算，可以得到每个中转站的利用率，从而确定哪些中转站可能成为供应链的瓶颈。

货物流通量分析不仅有助于确定瓶颈节点，还可以指导路径规划。如果某个中转站的利用率已经接近或达到了容量限制，就需要调整相关路径，以避免过度拥堵和延误，例如，可以考虑通过增加运输频率、改变运输路径或增加中转站的容量等方式来优化货物流通量，确保供应链的顺畅运作[2]。

1.3 运输成本分析

在供应链管理中，运输成本是一个关键因素，直接影响着路径规划和整体物流成本。需要对不同节点之间的运输成本差异进行分析，以找到最经济的路径选择。表3展示了不同节点之间的运输成本。

这些运输成本反映了从一个节点到另一个节点的运输成本，例如，从节点A到节点B的运输成本为50货币单位，为了找到最经济的路径选择，可以使用以下公式计算路径的总运输成本：

总运输成本=Σ（每段运输成本）。

其中，Σ表示对所有段的求和。

举例来说，如果考虑从节点A到节点D的两种可能路径：A→B→D和A→C→D，我们可以使用上述公式计算它们的总运输成本。

对于路径A→B→D：

总运输成本=50+80=130。

对于路径A→C→D：

总运输成本=70+55=125。

通过比较两条路径的总运输成本，可以确定路径A→C→D为更经济的选择，因为其总运输成本更低，通过这种方式，可以利用运输成本分析来选择最经济的路径，从而降低整体物流成本，提高供应链的效率。

2 物流选址优化

2.1 仓库位置选择

仓库位置选择是供应链管理中至关重要的一环。首先，需要收集关于供应链各节点之间距离和交通情况的数据。这包括各节点之间的实际距离、道路状况、交通拥堵情况、运输方式（如陆运、海运、空运）等信息。此外，还需要收集有关需求点（客户）的数据，包括需求点的位置、货物流通频率、每次交易的货物量等信息。例如，假设有一个供应链包括 A、B、C 三个节点，现在需要选择一个合适的仓库位置。收集的数据如下表4所示。

在确定最佳仓库位置时，可以采用多种数据处理与分析方法。一种常用的方法是基于距离和需求点分布的数学模型。这个模型可以通过公式表示，例如：

其中，D表示节点间的距离，（x1，y1）和（x2，y2）分别表示两个节点的坐标。通过计算节点间的距离，可以得到各节点之间的距离矩阵。

除了距离，还要考虑运输时间、需求量等因素，可以建立一个综合评价指标，例如：

其中，I表示综合评价指标，D表示距离，T表示运输时间，V表示平均每次的交易货物量。通过计算综合评价指标，可以评估每个节点作为仓库位置的适宜程度。

假设在上述案例中，节点A、B、C分别为可能的仓库位置候选。我们可以使用上述公式计算其综合评价指标，从而确定最佳仓库位置。节点 A 的综合评价指标计算如下：

类似地，可以计算节点B和节点C的综合评价指标：

通过比较各节点的综合评价指标，可以得出最佳仓库位置。在这个案例中，节点 C 的综合评价指标最低，因此可以选择节点 C 作为最佳仓库位置。这表明通过数据分析和计算，可以得出最佳仓库位置。选择合适的仓库位置能够减少货物的运输距离和运输时间，降低运输成本，提高供应链效率和客户满意度。因此，在供应链管理中，仓库位置选择是一个重要的决策问题，需要综合考虑多种因素，并采用合适的数学模型进行分析和评估。

2.2 配送中心布局

配送中心布局对供应链的效率和成本至关重要。首先，要收集关于货物流动、需求点分布和运输路径的数据。这包括需求点的位置、货物流量、运输距离、交通状况等信息。通过这些数据，可以分析货物流动频率、主要流动路径和各需求点之间的距离关系。例如，假设一个城市的供应链，包括需求点 A、B、C、D 四个地点，现在需要规划配送中心的位置和数量。收集的数据如表5所示。

在确定配送中心布局时，可以采用数学模型和优化算法。比较常用的方法是最小成本路径模型，它可以通过公式表示，例如：

其中，TC表示总成本，Cij表示从配送中心i 到需求点j的运输成本，Xij表示是否选择该路径（取值为0或1）。通过建立这样的数学模型，可以确定最佳配送中心位置和数量，以实现总成本最小化。

在上述例子中，有三个可能的配送中心位置候选，分别为X、Y、Z。我们可以使用上述最小成本路径模型计算它们的总成本，并比较各个方案的优劣。设配送中心位置X到需求点j的运输成本为CXj，则配送中心位置X到需求点A，需求点B，需求点C，需求点D的运输成本分别表示为CXA、CXB、CXC、CXD。总成本TCX为：

类似地，可以计算配送中心位置Y和Z的总成本TCY和TCZ。通过比较各个方案的总成本，可以确定最优配送中心布局。通过数据分析和计算，可以得出最优配送中心布局方案。合理的配送中心布局可以最大程度地减少货物的中转次数和运输路径的长度，降低运输成本，提高供应链的效率和灵活性[3]。

3 供应链协调与优化

在传统的供应链管理中，各个环节往往被独立优化，导致资源浪费和效率低下，这是因为在传统管理模式下，每个环节的决策往往都是基于本地信息和目标进行的，缺乏对整体供应链的全局考虑。而基于协同优化算法的供应链协调与优化模型则能够优化整个供应链，实现资源的最优配置和信息共享，从而提高供应链的整体效率和响应能力[4]。

传统的供应链管理常常存在这样的情况：每个环节都在追求自身利益最大化，却忽视了整体的利益最大化，比如，采购部门可能会以尽可能低的成本购买原材料，但这可能会导致库存过多，增加资金占用成本和库存成本；生产部门可能会为了追求生产效率而忽视及时交付的重要性，导致生产计划与实际需求脱节；而销售部门可能会过度承诺交货时间，增加供应链的不确定性，基于协同优化算法的供应链协调与优化模型可以解决这些问题。这个模型不再将供应链的各个环节看作孤立的部分，而是将其视为一个整体来优化，这意味着不同环节之间的决策将相互作用，以实现整体最优解。

为了实现这种协同优化，需要考虑多个因素，如供应商的供货能力、生产能力、销售预测、运输成本等，这些因素将构成一个复杂的优化问题，需要借助数学模型和优化算法来求解，需要建立一个数学模型来描述整个供应链系统，这个模型可以包括各个环节的决策变量、约束条件和目标函数。在一个简单的供应链模型中，可以将供应商的采购量、生产商的生产量和分销商的销售量作为决策变量，将供应链的利润作为目标函数。接着，需要选择合适的优化算法来求解这个模型。常见的优化算法包括线性规划、整数规划、动态规划等。这些算法可以针对不同的优化问题提供有效的求解方法，最后，考虑实际数据和约束条件。这些数据可能包括供应商的价格、生产商的成本、分销商的需求量等。同时，还需要考虑一些实际约束条件，如供应链的容量限制、生产周期、运输时间等。

例如，考虑一个简单的供应链模型，包括供应商、生产商和分销商三个环节，假设有以下数据：供应商提供零件的价格为50货币单位/件，生产商的制造成本为30货币单位/件，分销商的售价为80货币单位/件。每个月供应商能供应1 000件零件，生产商的产能为1 500件/月，分销商的销售需求为1 200件/月。运输成本如表6所示。

现在，通过协同优化算法来确定最优供应链决策，包括每个环节的采购量、生产量和销售量，以实现整个供应链的利润最大化，可以使用下面的公式来计算整体供应链的利润：

整体利润 = 收入 - 成本 - 运输成本。

其中，收入等于销售数量乘以售价，成本等于采购数量乘以采购价格加上生产数量乘以制造成本，通过不断调整各环节的决策，我们可以找到最优供应链配置方案，从而实现整体利润最大化，这就是基于协同优化算法的供应链协调与优化模型的核心目标和作用[5]。

4 结 语

本文以基于协同优化算法的供应链网络设计与管理为研究对象，通过对路径规划、物流选址、供应链协调与优化等方面的分析和探讨，提出了一种全新的解决方案，该方案能够有效应对传统供应链网络设计中存在的问题，提高供应链的运作效率和管理水平，具有重要的理论价值和实践意义，在未来的研究中，可以进一步探讨协同优化算法在其他领域的应用，为优化供应链管理提供更多思路和方法。

参考文献：

[1] 庄持．考虑中断风险的医药物流中心选址及配送路径协同优化研究[D]．北京：北京交通大学，2023.

[2] 晏榆洋，张浩，帅培．基于规划模型的运输网络最大流问题的分析研究[J]．物流科技，2024，47（8）：5-7.

[3] 俞启玟．基于区块链技术的食品可追溯供应链系统研究[J]．物流科技，2024，47（5）：124-127.

[4] 王群勇，孟雅婧，庞瑞芝．企业ESG表现对供应链网络地位影响研究：路径检验与机制分析[J]．现代财经（天津财经大 学学报），2024，44（4）：36-55.

[5] 王文利，李杰．基于复杂网络的突发事件下汽车产业供应链韧性研究[J]．供应链管理，2024，5（4）：63-77.