集装箱船舶配载问题的蚁群算法求解设想

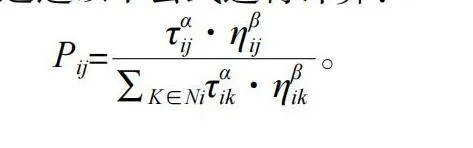
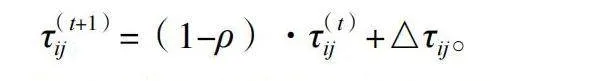
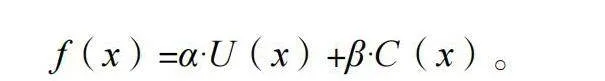
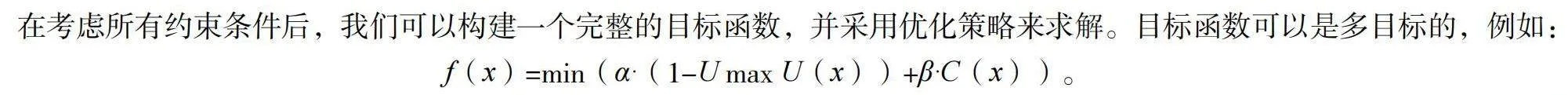
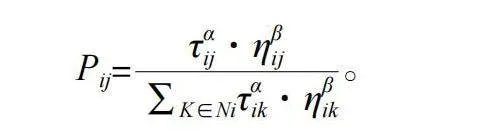
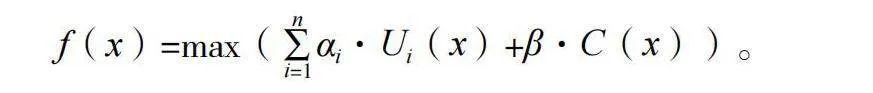
摘 要：文章探讨了蚁群算法在集装箱船舶配载问题中的应用。首先介绍了蚁群算法的基本原理及其在集装箱船舶配载问题中的应用背景，然后详细阐述了配载问题的数学建模情况，描述了蚁群算法的具体实现步骤，并通过案例分析，展示了蚁群算法在实际应用中的求解过程和应用效果，讨论了算法性能评估和不同情境的优化效果，探讨了蚁群算法的参数调优策略。

关键词：蚁群算法；集装箱船舶配载；数学优化建模；多目标优化；算法泛化能力

中图分类号：F552；U693.4 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.023

Abstract： This paper delves into the application of ant colony optimization （ACO） in the container ship loading problems. The article begins by introducing the fundamental principles of ACO and its application background in the container ship loading problems. It then provides a detailed exposition of the mathematical modeling of the loading problems， and describes the specific implementation steps of ACO. Through case studies， the paper illustrates the solution process and effectiveness of ACO in practical applications， discusses the performance evaluation of the algorithm and the optimization effects under different scenarios， and investigates strategies for parameter tuning within ACO.

Key words： ant colony optimization （ACO）; container ship loading; mathematical optimization modeling; multi-objective optimization;algorithm generalization capability

收稿日期：2024-04-18

作者简介：张 勇（1978—），男，山东菏泽人，青岛前湾集装箱码头有限责任公司，正高级工程师，研究方向：智慧港口建设与技术研究；陈进鹏（1983—），男，山东青岛人，青岛前湾集装箱码头有限责任公司，副高级工程师，研究方向：智慧港口建设与技术研究，徐振田（1994—），女，山东青岛人，青岛前湾集装箱码头有限责任公司，工程师，硕士，研究方向：智慧港口建设与技术研究。

引文格式：张勇，陈进鹏，徐振田．集装箱船舶配载问题的蚁群算法求解设想[J]．物流科技，2024，47（22）：89-93.

1 集装箱船舶配载问题的蚁群算法简介

1.1 蚁群算法的基本原理和应用背景

蚁群算法（Ant Colony Optimization， ACO）是一种模拟自然界蚂蚁觅食行为的优化算法。自提出以来，该算法历经改进和扩展，已成功应用于多个领域，被用于解决路径规划、网络路由、调度等问题。在优化问题中，蚁群算法凭借其独特的分布式决策和集体智能特性，展现出了强大的问题解决能力。

在集装箱船舶配载问题中，蚁群算法被用于优化货物装载方案，以达到节省空间、减少运输成本和提高效率的目的[1]。通过模拟蚁群的觅食行为，算法能够计算出更优的装载方案，在保证安全的前提下，提高船舶的装载效率。

1.2 蚁群算法在解决集装箱船舶配载问题中的优势和局限性

集装箱船舶的配载问题是一个复杂的优化问题，包括货物种类和尺寸的多样性、装卸顺序的约束、船舶稳定性的要求等，这些问题的复杂性要求算法能够优化多目标处理流程，并在有限时间内找到可行解。

蚁群算法在配载优化中的优势主要体现在以下几方面。

全局搜索能力：蚁群算法通过模拟蚂蚁的觅食行为，能够有效进行全局搜索，避免陷入局部最优解。

自适应调整：算法中的信息素更新机制能使优秀的解决方案得以加强，引导搜索过程向更优解的方向进行。

并行处理：蚁群中的每只蚂蚁可以独立进行路径选择，这种并行处理机制使得算法能够有效利用计算资源。

然而，蚁群算法在应用中也存在一些挑战和局限性。

收敛速度：在某些情况下，蚁群算法可能需要较多的迭代次数才能收敛得到较好的解，但这会增加计算时间。

参数调整：算法的性能很大程度上依赖于参数设置，如信息素挥发系数、启发式因子等，而这些参数的最优设置往往需要通过大量实验来确定。

问题规模：对于规模较大的问题，蚁群算法可能会因为计算资源限制而难以找到最优解。

2 集装箱船舶配载问题的数学建模

2.1 集装箱船舶配载问题的定义和目标

2.1.1 问题定义：集装箱船舶配载的基本概念

集装箱船舶配载问题是指在有限的船舶空间内，通过合理安排集装箱的装载位置，以实现高效运输的过程。这个问题涉及货物的种类、尺寸、重量、装卸顺序以及船舶的稳定性等多方面因素。在实际操作中，配载计划需要确保船舶的安全性、提高空间利用率，并尽量降低操作成本。

2.1.2 优化目标：最大化空间利用率、最小化操作成本等

集装箱船舶配载问题的优化目标通常包括以下几方面。

空间利用率最大化：尽可能多地装载货物，提高船舶的运输效率。

操作成本最小化：减少装卸货物所需的时间和劳动力，降低运输成本。

保证船舶稳定性：合理安排货物分布，确保船舶在各种海况下的稳定性。

满足服务需求：根据货物到达目的地的时间要求，合理安排装卸顺序。

2.1.3 目标的数学表达：目标函数的形式化描述

为了形式化描述上述优化目标，我们可以构建一个目标函数，通常采用线性或非线性形式来表达。例如，目标函数可以是空间利用率与操作成本的加权和：

f（x）=α·U（x）+β·C（x）。

其中，x表示配载方案，U（x）是空间利用率，C（x）是操作成本，α和β是权重系数，可以根据实际情况加以调整。

2.2 集装箱船舶配载问题的约束条件和目标函数

2.2.1 约束条件的分类和描述：物理、操作、法规等

构建数学模型时，需要考虑以下几类约束条件。

物理约束：包括集装箱的尺寸、重量限制，以及船舶的承重能力和空间限制。

操作约束：涉及装卸顺序、装卸设备的作业范围和效率等。

法规约束：考虑国际海事组织（IMO）等机构制定的运输规定和安全标准。

2.2.2 约束条件的数学模型

物理约束可以通过以下不等式来表示：

h min≤h（x）≤h max，

w min≤w（x）≤w max。

其中，h（x）和w（x）分别表示配载方案中集装箱的高度和宽度，h min、h max、w min、w max分别表示船舶空间的最小和最大限制。

操作约束可以通过以下方式来表达：

S（x）⊆SL，

F（x）⊆FL。

其中，S（x）表示配载方案中的货物装卸顺序，SL表示所有可能的装卸顺序集合；F（x）表示配载方案中的货物分布，FL表示所有可能的货物分布集合。

法规约束可以通过安全标准和运输规定的具体要求来表达，例如：

Ssafe（x）≥Srequired。

其中，Ssafe（x）表示配载方案所满足的安全标准，Srequired表示法规要求的最低安全标准。

2.2.3 目标函数的构建和优化策略

在考虑所有约束条件后，我们可以构建一个完整的目标函数，并采用优化策略来求解。目标函数可以是多目标的，例如：

f（x）=min（α·（1-U max U（x））+β·C（x））。

其中，U max是最大的空间利用率。优化策略可以采用线性规划、整数规划、启发式搜索等方法，根据问题的规模和复杂性选择合适的算法。

通过上述数学建模，我们可以将集装箱船舶配载问题转化为一个可求解的优化问题，为后续的算法设计和求解提供基础。

3 蚁群算法在集装箱船舶配载问题中的应用

3.1 蚁群算法的具体实现步骤

为了更详细地说明蚁群算法的具体实现步骤，我们将对每个阶段进行深入分析，并为其提供相应的公式和推理过程。

3.1.1 算法初始化

3.1.1.1 参数设定

在蚁群算法中，关键参数的设定对算法性能至关重要。以下是一些主要参数的设定方法。

蚂蚁数量（n）：蚂蚁数量决定了搜索空间并行探索的广度。蚂蚁数量通常需要根据问题的复杂性和求解空间的大小加以调整。

信息素挥发系数（ρ）：信息素挥发系数决定了信息素的遗忘速度，其值通常为0～1。较高的挥发系数会使算法更倾向于探索新解，而较低的挥发系数则有助于维持已有的优秀解。

启发式因子（η）：启发式因子反映了问题特定知识的权重，它通常与路径选择概率计算中的距离或成本成反比。

3.1.1.2 信息素初始化

信息素矩阵τ用于存储每条路径上的信息素浓度，其初始化通常采用均匀分布的方式进行，即对于从i到j的所有路径，初始信息素τij（0）被设定为相同的值τ0。

3.1.2 蚂蚁构建解的过程

3.1.2.1 路径选择机制

蚂蚁在构建解时，选择下一个节点的概率P可以通过以下公式进行计算：

3.1.2.2 信息素更新规则

信息素更新包括两部分：蒸发和沉积。

蒸发：信息素随时间自然减少，更新公式为τij（t+1）=（1-ρ）·τij（t）+△τij。

沉积：蚂蚁在路径上留下信息素，沉积量与路径的质量成正比，更新公式为τij（t+1）=τij（t）+△τij，其中△τij是所有蚂蚁在路径（i，j）上留下的信息素总量。

3.1.3 算法迭代过程

3.1.3.1 迭代控制

在每次迭代t中，所有蚂蚁根据路径选择机制构建解，并更新信息素。迭代过程可以表示为以下步骤。

a.每只蚂蚁根据当前信息素和启发式信息构建解。

b.更新信息素矩阵τ。

c.评估所有解的质量，并记录当前迭代的最佳解。

d.如果达到终止条件，则停止迭代；否则，继续下一次迭代。

3.1.3.2 解的改进和优化

在迭代过程中，可以引入局部搜索策略来改进解。例如，使用2-opt交换操作，可以从当前解中选择两条边进行交换，以探索新的求解空间。

3.1.4 算法终止条件和解的评价

算法的终止条件可以是达到预设的迭代次数T，或者当前迭代中解的质量改善小于一个阈值。

解的评价需要根据问题的目标和约束来确定。例如，集装箱船舶配载问题的目标函数可以表示为：

其中，x是配载方案，Ui（x）是第i个目标的值（如空间利用率），C（x）是操作成本，αi和β是目标的权重系数。

通过上述详细的推导和解释，我们可以更加清晰地理解蚁群算法在集装箱船舶配载问题中的应用。这些步骤和公式为算法的实现和分析提供了坚实的理论基础。

3.2 蚁群算法在集装箱船舶配载问题中的求解过程和效果展示

为了具体展示蚁群算法在集装箱船舶配载问题中的应用，我们设计了一个案例。在这个案例中，假设有一艘中型货船，需要装载3 000个集装箱，这些集装箱的尺寸和重量各不相同，且每个集装箱都有特定的目的地和交付时间窗口。我们的目标是通过优化配载方案，实现船舶空间利用率的最大化和整体操作成本的最小化[2]。

在算法初始阶段，每只蚂蚁随机在船舶的仓位图中移动，根据信息素浓度和启发式信息（如集装箱尺寸与仓位的匹配度）选择放置集装箱的位置。随着迭代的进行，那些能够实现空间利用率最大化和成本最小化的配载方案会在信息素矩阵中积累更多信息素，从而吸引更多蚂蚁。这个过程可以用以下伪代码表示。

初始化信息素矩阵τij：

对于每次迭代t=1，2，…，T；

对于每只蚂蚁i=1，2，…，n；

随机选择起始仓位。

当所有集装箱都未放置时：

根据公式Pij选择下一个仓位j；

放置集装箱到仓位j；

根据公式τij（t+1）=（1-ρ）·τij（t）+△τij更新信息素矩阵τ；

记录最佳配载方案；

返回最佳配载方案。

通过多次迭代，蚁群算法逐渐收敛到一个或几个优秀的配载方案。

3.2.1 求解过程中的关键步骤和决策点

蚁群算法的求解过程包含几个关键步骤，每个步骤都涉及重要的决策点。

路径选择（Path Selection）：每只蚂蚁都会根据信息素浓度和启发式信息来选择下一个仓位放置集装箱。路径选择的概率由以下公式决定：

其中，Pij是蚂蚁从仓位i移动到仓位j的概率，τij是路径i到j的信息素浓度，ηij是启发式信息（例如，两个仓位之间的距离或集装箱尺寸的匹配度），α和β是信息素和启发式信息相对重要性的权重，Ni是蚂蚁当前所在的仓位i的所有可行邻居仓位集合。

信息素更新（Pheromone Update）：每当一只蚂蚁完成一个配载方案后，它就会在所经过的路径上释放信息素，同时，信息素会随时间推移而挥发。信息素更新可以用以下公式表示：

其中，ρ是信息素挥发系数，△τij是所有蚂蚁在路径i到j上释放的信息素总量。

解的改进（Solution Improvement）：在某些情况下，即使信息素更新，算法也可能产生局部最优解。这时，可以采用局部搜索策略来改进当前的配载方案。例如，可以使用2-opt交换操作，即从当前方案中选择两个集装箱并交换其位置，以探索解空间的其他区域。

3.2.2 算法性能的评估：结果对比、效率分析

解的质量可以通过以下目标函数来评估：

其中，f（x）是目标函数，Ui（x）是第i个目标的值（如空间利用率或满足特定要求的集装箱数量），C（x）是操作成本，αi和β是目标的权重系数。

算法的收敛速度可以通过记录每次迭代后的最优解质量来分析。如果算法可以在迭代过程中快速找到高质量的解，并且在随后的迭代中只有微小的改进，这表明算法的收敛速度较快。

3.2.3 算法在实际应用中的表现和改进

在实际应用中，蚁群算法可能需要根据具体问题加以调整和改进。例如，可以引入新的启发式信息，或者调整信息素更新规则，以适应特定问题的特点。此外，可以考虑结合其他算法，如遗传算法、模拟退火等，以提高算法的搜索能力和解的质量。

通过这些改进，蚁群算法在集装箱船舶配载问题中的应用将更加有效和可靠。实际应用的案例分析结果表明，蚁群算法能够在合理的时间内找到高质量的配载方案，从而提高物流效率并降低运输成本。

4 集装箱船舶配载问题的蚁群算法优化方案探讨

4.1 针对集装箱船舶配载问题的蚁群算法参数调优策略

4.1.1 参数调优的重要性和影响

在解决集装箱船舶配载问题时，蚁群算法的性能会受多种因素影响，其中参数设置至关重要。参数调优对于提高解的质量、加快收敛速度、避免陷入局部最优解具有显著影响。正确的参数设置能使蚁群算法更有效地搜索解空间，以探寻最佳配载方案，同时减少计算资源的消耗。

4.1.2 蚁群算法参数的分类和功能

蚁群算法中的关键参数通常包括如下几个方面。

蚂蚁数量（n）：蚂蚁数量决定了算法进行空间搜索的解的广度。较多数量的蚂蚁可以增加搜索的多样性，提高全局最优解的搜寻概率，但也会增加计算的复杂度。

信息素挥发系数（ρ）：该参数控制信息素随时间的衰减速度，影响算法的探索与开发平衡。较高的挥发系数会使算法更倾向于探索新解，较低的挥发系数则有助于算法在优秀解附近进行深入搜索[3]。

信息素重要度（α）和启发式信息重要度（β）：这两个参数分别控制信息素和启发式信息在蚂蚁路径选择中的影响力。信息素重要度较高时，蚂蚁更倾向于选择信息素浓度高的路径；启发式信息重要度较高时，蚂蚁更倾向于根据问题特性（如距离、成本等）选择有利路径。

局部搜索策略参数：如局部搜索的概率或2-opt交换操作的频率，这些参数可以影响算法挑选局部最优解的能力，提高搜索的深度以及解的质量。

4.1.3 参数调优的方法和策略

有效的参数调优方法有如下几种。

网格搜索（Grid Search）：通过遍历预定义参数范围内所有可能的组合，网格搜索可以找到最优参数设置。这种方法简单直观，但计算量可能很大。

随机搜索（Random Search）：与网格搜索相比，随机搜索在参数空间内随机选择参数组合，可以更快地找到有效的参数设置，尤其是在参数空间很大时。

遗传算法（Genetic Algorithm）：通过模拟自然选择和遗传机制，遗传算法可以在多代迭代中优化参数。这种方法可以适应复杂的参数交互，并找到全局最优解。

贝叶斯优化（Bayesian Optimization）：利用概率模型和高斯过程来预测参数设置对性能的影响，贝叶斯优化可以有效平衡探索和开发，减少搜索次数。

4.1.4 参数调优的实验结果和分析

实验可以通过改变单一参数或多个参数的同时变化来进行。通过对比不同参数设置下的算法性能，我们可以得出以下结论。

蚂蚁数量的影响：实验可能表明，随着蚂蚁数量增加，解的质量会先提高再趋于稳定。因此，存在一个最优的蚂蚁数量，能使算法保持较高的解的质量，同时使计算效率最高。

信息素挥发系数的影响：实验结果可能显示，适中的信息素挥发系数能够在探索与开发之间取得平衡，避免算法过早收敛到局部最优解，同时保持对优秀解的记忆。

信息素与启发式信息重要度的影响：实验可能会揭示信息素和启发式信息重要度之间的最佳比例，这取决于问题的特性和解的空间结构。

局部搜索策略参数的影响：实验可以评估局部搜索策略参数对解的质量的影响，找到不同情境下最有效的局部搜索频率和操作。

通过对实验结果的详细分析，我们可以找到最佳参数配置，提高蚁群算法在集装箱船舶配载问题中的应用价值。[4]

4.2 结合实例分析，探讨蚁群算法在不同情境下的优化效果

4.2.1 蚁群算法在不同情境下的应用案例

通过以下案例，我们可以分析蚁群算法在不同情境下的优化效果。

多样化货物装载：针对不同尺寸和重量的集装箱，蚁群算法可以通过调整信息素和启发式信息的权重来优化路径选择，从而找到空间利用率最大化的配载方案。

紧急货物优先：当有紧急货物需要优先装载时，算法可以通过引入优先级规则和调整信息素更新策略来确保紧急货物得到优先处理。

稳定性优先：在装载方案中，算法可以通过加入稳定性约束和调整局部搜索策略来确保船舶的稳定性，同时提升空间利用率。

4.2.2 针对特定情境的算法改进和定制

根据特定情境的需求，我们可以对蚁群算法进行改进和定制，以提高其在特定问题上的优化效果。

引入优先级规则：为紧急货物设置更高的优先级，确保其能够优先装载，同时调整信息素更新策略以反映这一优先级。

稳定性约束优化：在目标函数中加入对船舶稳定性的约束，确保装载方案具有安全性，同时通过调整启发式信息来满足稳定性要求。

动态调整参数：根据货物的特性和装载进度，动态调整算法参数以适应变化，如根据货物多样性调整信息素和启发式信息的权重。

通过这些改进和定制，蚁群算法能够更好地适应不同的配载情境，提供更加精确可靠的优化方案。这不仅可以提高物流效率，还有助于降低运输成本和提高安全性。

5 结 论

蚁群算法作为一种启发式搜索算法，在集装箱船舶配载问题中展现出了显著的应用潜力，通过信息素沉积与挥发机制，平衡探索新解和利用已知优秀解的能力。参数调优策略的引入可以进一步增强算法的适应性和鲁棒性，使得算法能够在不同的问题情境下保持高效的搜索性能。此外，通过与其他优化技术结合，如局部搜索策略和遗传算法，蚁群算法在求解过程中表现出了更高的灵活性和解的质量。未来随着研究的深入，我们期待蚁群算法能够在集装箱船舶配载问题上取得更多突破，为物流行业的持续发展和创新做出更大的贡献。

参考文献：

[1] 张煜，李俊，徐进，等．港航多视角下内河集装箱船舶配载决策[J]．计算机工程与设计，2021，42（1）：76-82.

[2] 王志超，丁一．考虑箱区作业均衡的自动化码头集装箱船舶配载计划[J]．计算机应用，2021，41（S2）：299-303.

[3] 李俊，张煜，计三有，等．多箱型内河集装箱船舶配载决策研究[J]．交通运输系统工程与信息，2019，19（1）：200-207.

[4] 郑斐峰，蒋娟，梅启煌．最小化集装箱运输成本的配载优化[J]．计算机科学，2019，46（6）：239-245.