Python在运输问题中的应用研究

摘 要：文章将深入研究Python Tkinter图形用户界面库和Pulp库在运输问题中的应用情况。首先，我们对运输问题的基本概念和分类进行了详细介绍，以帮助读者理解这一领域的基础知识和核心要点。随后，我们重点探讨了该如何利用Pulp库结合Tkinter图形用户界面库来解决运输问题。通过案例研究的方式，展示了Python Tkinter库在实际运输问题中的灵活应用，并评估了其在处理这些问题时具备的性能和效果。此外，我们还将对Python Tkinter库在解决运输问题中的潜力和未来发展方向进行讨论。

关键词：运筹学；运输问题；用户界面

中图分类号：F252.1 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.021

Abstract： This paper investigates the practical applications of Python Tkinter GUI library and Pulp library in transportation problems. Firstly， we introduce the basic concepts and classifications of transportation problems in detail to help readers understand the basic knowledge and core points of this field. Then， we focus on discussing how to use Pulp library and Tkinter GUI library to solve transportation problems. After that， through case studies， we demonstrate the flexible application of Python Tkinter library in practical transportation problems， and evaluate its performance and effectiveness in dealing with these problems. Finally， we discuss the potential and future development directions of Python Tkinter library in transportation problems.

Key words： operational research; transportation problems; user interface

收稿日期：2024-04-26

作者简介：努日曼古丽·牙森（1983—），女，维吾尔族，新疆巴音郭楞蒙古自治州人，广州商学院信息技术与工程学院，助教，硕士，研究方向：应用数学；肉孜买买提·马合木提（1984—），男，维吾尔族，新疆和田人，广州商学院信息技术与工程学院，副教授，博士，研究方向：应用数学。

引文格式：努日曼古丽·牙森，肉孜买买提·马合木提．Python在运输问题中的应用研究[J]．物流科技，2024，47（22）：82-85.

0 引 言

Python作为一种流行编程语言，凭借其简洁、易读和高效的特点，已被广泛应用于解决各种问题[1-4]，包括微积分、线性代数、微分方程及运筹学。Python的特点使其成为了解决运输问题的理想选择。Tkinter是Python的标准GUI库，用于创建图形用户界面，使用Tkinter可以轻松创建用户友好的界面，使问题更加直观且易于理解，在各领域都取得了良好的应用效果[5-6]。

运输问题是物流、供应链和许多其他领域经常遇到的问题[7]。随着全球化和电子商务的快速发展，运输问题的解决变得越来越重要了。在运输问题中，Tkinter可以用于创建更加直观和易于理解的界面，使得运输问题的求解过程变得更加便捷。

SciPy库和Pulp库在解决线性规划问题方面都有其独特的应用。首先，SciPy库是一个基于Python的科学计算库，它提供了丰富的数学工具，包括线性代数、统计分析、优化、信号处理等。在解决线性规划问题时，SciPy库可以使用其优化模块中的线性规划求解器，这些求解器基于数学优化算法，如单纯形法、内点法等，能够找到线性目标函数在给定线性约束条件下的最优解[8]。SciPy库的优点在于其强大的数学计算能力，能够处理各种复杂的线性规划问题。

Pulp库则是一个专门用于创建和求解线性规划整数规划问题的Python库。它提供了一个简洁的语法，使得定义决策变量、目标函数和约束条件变得非常方便；同时，Pulp库支持多种类型的决策变量，包括连续型、整数型、二进制型等，使得它能够适用于更多类型的优化问题[6]；此外，Pulp库还支持多种求解器，包括内置的求解器以及外部的求解器，如CBC、GLPK、CPLEX、Gurobi等，使得用户可以根据问题的特性和需求选择合适的求解器。

在解决线性规划问题时，Pulp库和SciPy库都可以找到最优解。然而，对于某些特定问题，如整数规划问题或运输问题，Pulp库更加适合。因为Pulp库集成了多种适用于不同问题的求解器，包括线性规划、整数规划、混合整数规划等，使得其能够针对运输问题提供专门的求解器，从而提高求解效率和准确性。SciPy库的优化模块虽然也支持多种优化方法，但可能仍缺乏针对运输问题的特定求解器。

本文旨在为运输问题的解决提供一种新的方法和工具，并推动Python在相关领域的应用和发展。

本文的结构安排如下：在第二节简单介绍运输问题，并阐述Python在运输问题中的必要性；在第三节详细介绍界面的建立和核心函数；在第四节通过实际案例来展示此界面在运输问题和分配问题中的实际应用，并评估其性能和效果；最后，讨论Python Tkinter的应用及其未来的研究方向。

1 运输问题及Python的必要性

运输问题的数学模型如下所示。

其中，xij为决策变量，cij为从第i个产地运输到第j个销售地所发生的运价。当表达式（2）和（3）同时满足等式条件时，该问题被称为平衡问题。平衡问题通常通过表上作业法来解决，然而，在处理大规模运输问题时，如何制定最优运输方案成为了一个突出的挑战，特别是因为不同地点的需求量和供应量之间可能存在不一致性，导致需求与供应不平衡，即表达式（2）和（3）中有一个不满足等式条件。为有效解决这个问题，我们通常需要先通过某种方法将问题转化为平衡问题，然后再进行求解。

对这个问题，Python的Tkinter库和Pulp库可以提供强大的工具。其中Tkinter库主要用于图形用户界面（GUI）的开发，Pulp库则提供简洁易用的接口来定义线性规划问题。在这种情况下，我们可以使用这两个库来完成不同的任务。首先，使用Tkinter库可以创建一个图形用户界面，这样用户就可以输入其数据，例如运价、需求量和提供量，并查看结果，能使得程序更易于使用和理解，尤其是对于非技术用户而言。其次，我们可以使用Pulp库中的优化算法来解决这个平衡和不平衡的问题，特别是Pulp库有多种线性规划求解器，如CBC、GLPK等。这些求解器经过优化，能够高效处理大规模线性规划问题。

2 方案分析及主要技术实现过程

2.1 方案分析

本文研究一个结合Tkinter模块与Pulp模块的实践项目，旨在通过构建一个简易的用户界面来求解运输问题和分配问题。本文不仅提供了直观的用户体验，还力图融合教育意义，使得学生在实践中能够掌握Python基础语言、Tkinter界面设计和Pulp优化求解模块的应用。

首先，Tkinter模块是Python的标准GUI库，易于学习和使用。通过Tkinter构建的界面，用户可以轻松输入问题参数，而无需具备复杂的编程背景。界面友好、操作简便的特性，有助于提高用户（尤其是学生）的参与度和学习兴趣。

其次，Pulp模块的应用是本文的核心部分。作为一个强大的线性规划求解器，Pulp能够有效处理运输和分配问题，这些问题在实际生活和工作中广泛存在。通过Tkinter界面与Pulp模块结合，学生可以在实践中理解并掌握线性规划问题的建模与求解过程，这对其未来的学术研究和职业发展大有裨益。

此外，通过区分平衡问题、不平衡问题和分配问题，学生可以更加深入地理解这些概念之间的差异，同时，这种项目导向的学习方式也能够激发学生的学习热情，使他们能够在实践中发现问题、解决问题，从而实现知识的内化与能力的提升。

2.2 主要技术实现过程

先通过tkinter.Tk定义一个窗口，参考代码如下。

Import tkinter as tk

root = tk.Tk（）

root.title（“运输问题”）

接下来，通过tk.Label、tk.Text、tk.Entry和tk.Button函数，可以创建界面输入参数所用的文本框和按钮，并通过tk.Listbox函数创建输出列表（如图1所示）。

具体输入方法我们将在第4节举例操作中进行说明，这里主要解释程序内部的运行过程。当我们录入完所有参数并按求解按钮时，将按照下面步骤运行程序。

首先，把运价表里的参数赋给cij（i=1，2，...，n；j=1，2，...，m），其中n，m分别由运价表的行数和列数来确定，提供量的参数和需求量的参数分别赋给ai（i=1，2，...，n）和bj（j=1，2，...，m）。

其次，创建线性规划问题。通过import pulp导入Pulp 库，并通过prob = pulp.LpProblem（name，sense）函数创建线性规划问题。由于我们解决的问题是运输问题，因此参数设置为：

name = 'Transportation Problem'，

sense = pulp.LpMinimize。

然后，按照已录入数值的大小，创建决策变量的数列。参考如下代码：

var = [[pulp.LpVariable（f'x{i}{j}'， lowBound=0， cat=pulp.LpInteger） for j in range（col）] for i in range（row）]。

其中，lowBound=0表示决策变量满足xij≥0的条件，cat=pulp.LpInteger表示决策变量是整数。

再次，创建目标函数和约束条件。这些步骤可以通过Pulp库里的lpDot函数和lpSum函数来实现，参考如下代码：

prob += pulp.lpDot（var，c）

for i in range（row）：

prob += （pulp.lpSum（var[i]） == a[i]）

for j in range（col）：

prob += （pulp.lpSum（[var[i][j] for i in range（row）]） == b[j]）

最后，可以通过prob.solve（）函数来求解运输问题的最优方案。

代码中可以应用if语句来判断输入问题是否为平衡问题，如果是平衡问题，上面的代码就是可行的；如果提供量大于需求量，可以将上面代码中的lpSum（var[i]） == a[i]换成lpSum（var[i]） < a[i]；如果需求量超过提供量，则将代码中的pulp.lpSum（[var[i][j] for i in range（row）]） == b[j]换成pulp.lpSum（[var[i][j] for i in range（row）]） < b[j]即可。这一步可以通过if语句自动实现，无需手动调整。因此，对于不平衡问题，此程序具有可行性。

3 举例操作

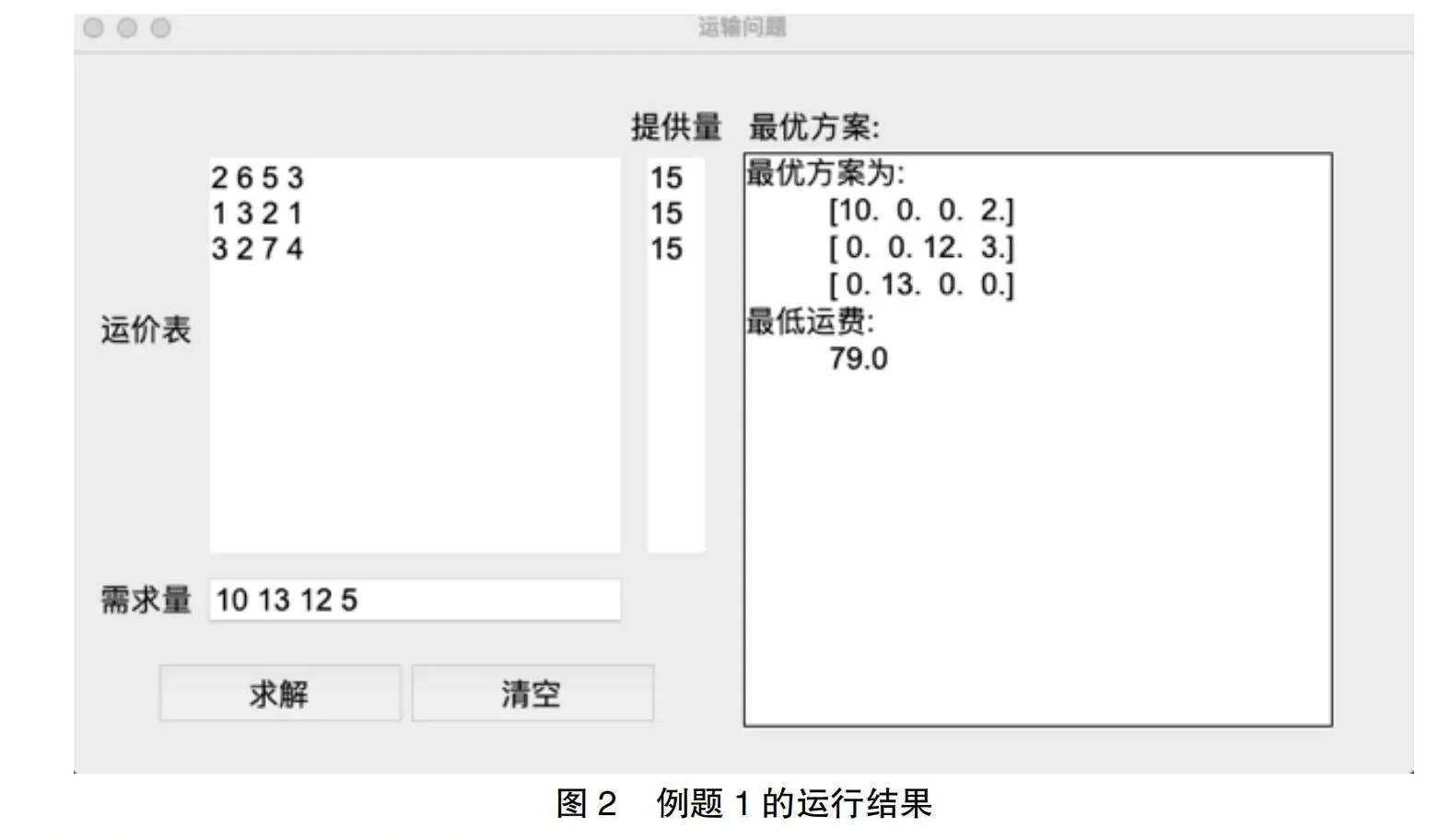
例题1. 某部门有Ai（i=1，2，3）3个生产同类产品的工厂Ai（i=1，2，3），生产的产品有4个销售点Bi（i=1，2，3，4）出售，各工厂的生产量、各销售点的销售量以及各工厂到各销售点的运价（元/吨）如表1所示。

试求出最优运输方案。

我们运行程序后，出现图1所示的窗口；将数据输入对应的文本框，并按<求解>按钮（如图2所示），可以算出此问题的最优方案和总运价费。数字之间用空0ef7f9d786ca9a4a4b46c1472d43b339格来分割，如果出现数字不完整的情况就会出现相应的错误提醒。

除了运输问题，我们还可以运算分配问题的最优方案。

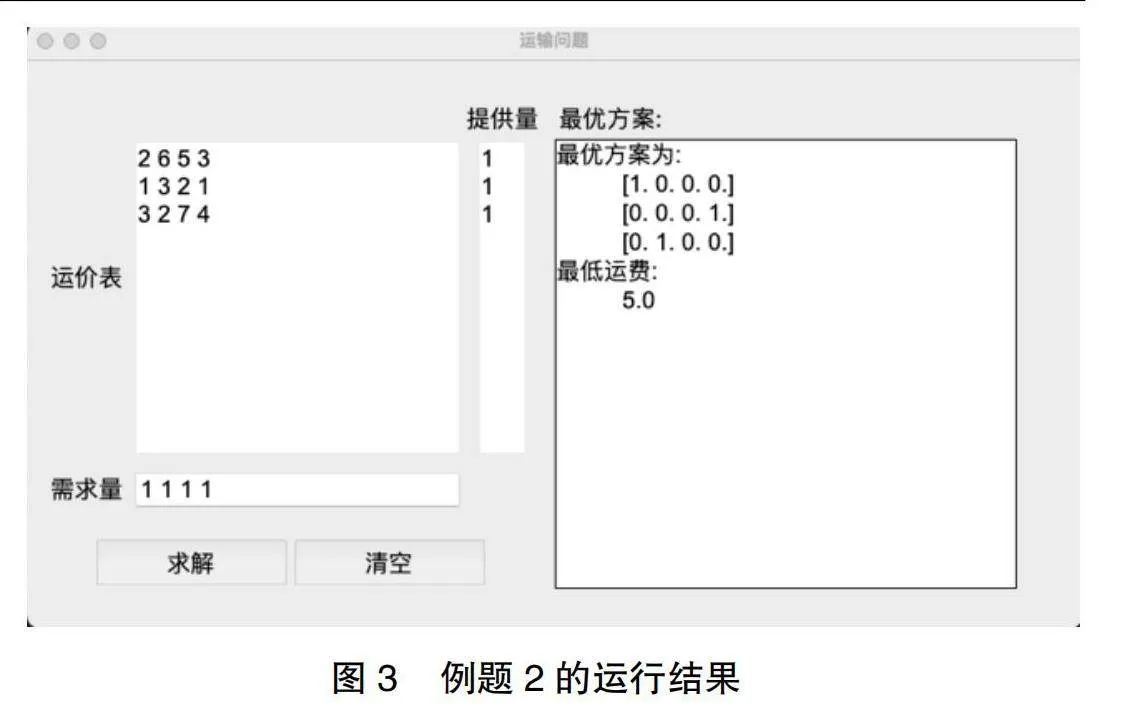
例题2. 有一份材料需翻译成A，B，C，D四种语言，现有3个人，一个人完成一项任务，问如何分派任务总时间最少，所需时间如表2所示。

其实分配问题是运输问题中的特殊情况，只要把提供量和需求量都设置为1，就可以计算分配问题了。运行结果如图3所示。

如图3所示，当甲完成A，乙完成D，丙完成B时所需时间最少为5 h。

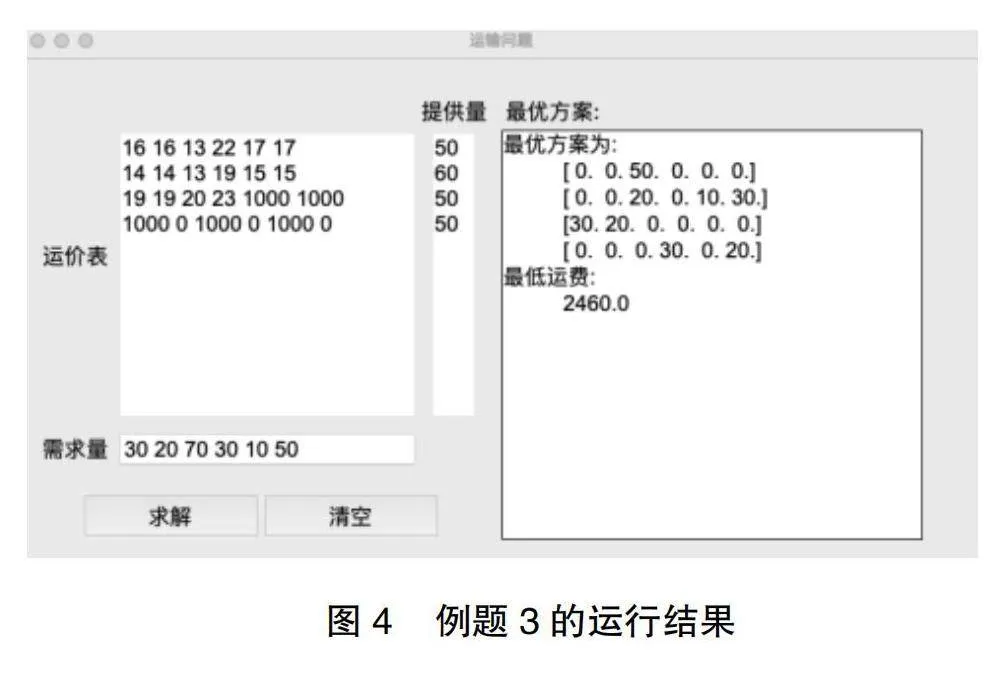
例题3. 有甲、乙、丙三个化肥厂供应Ⅰ、Ⅱ、Ⅲ、Ⅳ四个地区的农用化肥，三个工厂每年各自的产量分别为50万吨、60万吨和50万吨。四个地区的需求量分别为Ⅰ地区最高50万吨，最低30万吨，Ⅱ地区为70万吨，Ⅲ地区为30万吨以下，Ⅳ地区不低于10万吨。已知从各化肥厂到各地区，单位化肥的运价如表3所示。如何调运，可使总调运费用最小？

由于产量小于需求量，因此虚设一个虚拟化肥厂“丁”。按照最低需求和最高需求，可以写平衡表如表4所示。

其中“丁”是虚拟产地，M是任意大的正数。由于需求地Ⅰ的最低需求是30万吨，因此第2列的30万吨不可以由虚拟产地“丁”所提供。因此，我们把产地“丁”到销地I的运价设为任意大的正数M。销售地Ⅱ和Ⅳ也是同一个道理。运行结果如图4所示。

4 结 论

本文使用Tkinter模块构建了一个简单的界面，并利用Pulp模块求解了运输问题和分配问题。这个界面使用起来非常方便和简单，效果也非常好，在代码编写过程中，学生可以掌握Python基础语言、Tkinter模块和Pulp模块的使用；同时，这个界面也可以帮助学生分辨平衡问题、不平衡问题和分配问题的区别，对培养学生的学习热情起到了很大的作用。在未来的工作中，我们将进一步研究Tkinter库在目标规划和动态规划中的应用。

参考文献：

[1] 谭立云，张晓瑾．python在极限运算中的应用[J]．科学技术创新，2020（27）：18-20.

[2] 刘双．基于Python的微分方程在多领域中的应用[J]．黑龙江科学，2022，13（7）：162-164.

[3] 赵禹琦．基于Python软件求多元隐函数的偏导数[J]．新型工业化，2021，11（8）：224-226.

[4] 宋婷婷，王琳琳．Python语言在高等数学积分教学中的应用探析[J]．电脑知识与技术，2023，19（25）：118-121.

[5] 高秀艳．基于Tkinter的多语语料库分段与对齐工具实现研究[J]．河北软件职业技术学院学报，2020，22（3）：5-8.

[6] 肉孜买买提·马合木提．Python在运筹学教学中的应用[J]．现代职业教育，2022（6）：88-90.

[7] 胡运权．运筹学基础及应用（第六版）[M]．北京：高等教育出版社，2014.

[8] 罗伯特·约翰逊．Python科学计算和数据科学应用（第2版）[M]．黄强，译.北京：清华大学出版社，2022.