校车站点布局的仿真模拟

摘 要：文章针对学生上下学的路径问题，基于K-means算法和蚁群算法进行研究，通过使用三阶段布局法（确定候选站点、确定初始候选站点的布局方法、站点布局优化）确定站点的位置设置，采用MATLAB仿真软件对K-means算法、蚁群算法进行模拟，并对调查数据进行分析。文章主要研究这两种方法下的路径优化方式，通过实验计算，证明了蚁群算法得出的学生上下学路径要优于K-means算法下的路径，K-means算法使得每条路径人数分布不均匀且路程不相近；而蚁群算法使得每条路径学生的搭乘数均等，校车走过的路程相近。

关键词：MATLAB；K-means算法；蚁群算法；路径优化

中图分类号：F540.5 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.020

Abstract： This paper conducts a study on the path problem of students going to and from school based on K-means algorithm and ant colony optimization. It uses the three-stage layout method （determining candidate stat3ujx3VdVQDUJAMoyf8nAYKCtoCg3EK5o3w/ZikuhB8U=ions， determining the layout method of initial candidate stations， optimizing the station layout） to determine the location of the station. MATLAB simulation software is used to simulate the K-means algorithm and ant colony optimization， and analyze the survey data. The main focus of this article is on path optimization under these two methods. Through experimental calculations， it has been proven that the students' path to and from school under the ant colony optimization is better than that under the K-means algorithm. The K-means algorithm results in uneven distribution of students on each path and uneven distances， while the ant colony optimization ensures that the number of students on each path is equal， and the distance traveled by the school bus is similar.

Key words： MATLAB; K-means algorithm; ant colony optimization; path optimization

收稿日期：2024-04-25

作者简介：刘晓龙（1991—），男，宁夏吴忠人，宁夏理工学院机械工程学院，讲师，硕士，研究方向：机械自动化、路径优化；王学军（1984—），男，宁夏固原人，宁夏理工学院机械工程学院，副教授，硕士，研究方向：智能交通系统、物流系统设计。

引文格式：刘晓龙，马旭琴，王学军．校车站点布局的仿真模拟[J]．物流科技，2024，47（22）：76-81.

0 引 言

为适应城市人口增长带来的教育需求增加的问题，各大高校近年来逐渐开始扩大办学规模，改善现有教学环境，提高教学质量，同时，为了更好地服务于社会和学生，保障教师和学生的工作和学习效率，各大高校开始实施校车服务，合理的站点布局对校车路径优化起着至关重要的作用。

任腾等（2022）研究了面向冷链物流配送路径优化的知识型蚁群算法[1]；柳伍生等（2021）研究了“无人机-车辆”配送路径优化模型与算法[2]；张冬青等（2021）研究了考虑时空相关随机行驶时间的车辆路径问题模型与算法[3]；王勇等（2022）研究了基于客户信用度的物流配送车辆路径问题[4]；张春玲等（2021）针对物流配送中心选址问题进行研究[5]；Meng等（2020）将改进的K-均值算法应用于公务车联网环境[6]；Fadda等（2020）针对具有相关随机旅行成本的随机多径旅行商问题进行了研究[7]；周果等（2022）对于多对多越库配送绿色车辆路径问题及算法进行了研究[8]；胡小建等（2022）基于时间窗约束的多人多储位拣选路径优化模型及改进遗传算法应用进行了研究[9]。

1 路径优化算法及对应的模型建立

1.1 K-means算法

聚类分析，也称为群分析[10]，是一种统计分析方法，主要通过对已有数据进行分类，使具有相似特征的数据聚类到一起，分组为不同的簇，同一簇内的对象具有相似的属性，通过不断迭代来进行聚类，直到满足某个结束条件，从而输出一个聚类结果。

轮廓系数（Silhouette Coefficient Index）是一种聚类评估指标，用于评估数据的聚类效果。轮廓系数的取值范围一般为[-1，1]，当轮廓系数接近1时，表示聚类效果较好。轮廓系数表达式为：

式中，i表示其中的某一个点；a（i）表示i到所有其所属的簇中其他点的距离；b（i）表示i到某一个不包含它的簇内所有点的平均距离。

1.2 K-means算法的模型建立

K-means算法的核心思想为[11]：在给定n个数据点{x1，x2，...，xn}中，找到K个聚类中心{a1，a2，...，ak}，使得每个数据点与它最近的聚类中心的距离平方和最小，并将该距离平方和称为目标函数，记为Wn，数学表达式为：

在校车站点布局的问题中，数据集中聚类的组别数为已定的站点数，迭代计算得出的聚类中心为校车站点，聚类目标函数为每个站点之间的距离和最小，数学表达式为：

式中，CN为学生站点数；Ni为第i个学生站点（i=1，2，...，CN）；D（CN，Ni）为该站点到第i个车站的距离；Mki=0或1，第k个站点被分配到第i个站点上则为1，否则为0。

一般情况下，聚类算法采用距离函数（多为欧氏距离）进行计算，判断数据之间的距离，但该算法也有很多缺点，其中包括需要提前人为设置确定K值、严重依赖于初始簇中心点的选取、聚类算法无法发现任意形状的簇以及易收敛于局部最优解等，以下为空间之间的距离公式表达式。

n维空间上点a（X11，X12，…，X1n）与b（X21，X22，…，X2n）的欧氏距离数学表达式为：

1.3 蚁群算法

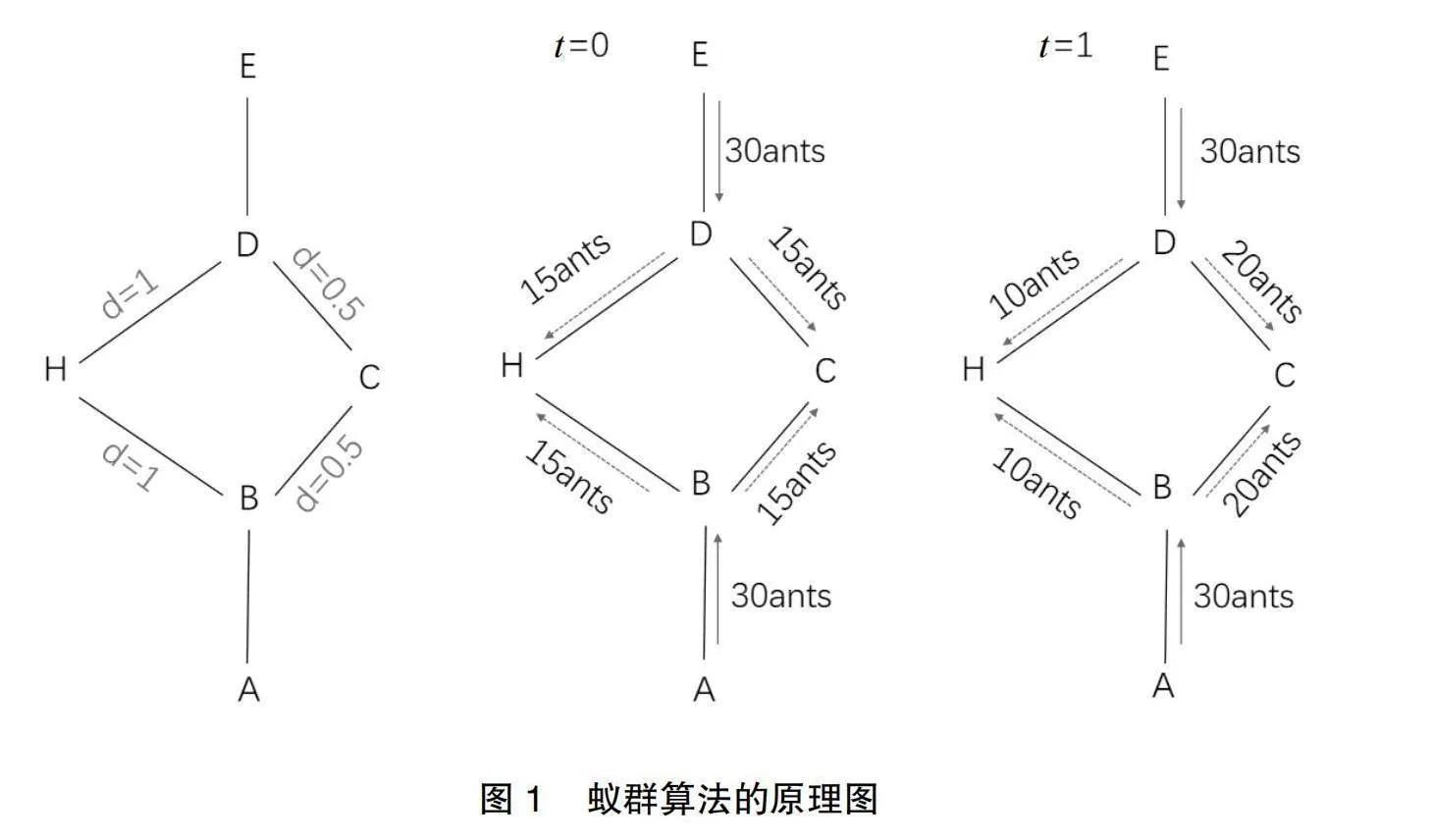
蚁群算法的原理是模拟自然界中蚂蚁的觅食行为[12]，蚂蚁在寻找食物的过程中，会在其所经过的路径上遗留一种叫做信息素的化学物质，这种信息素对于蚂蚁来说是一种重要的通信方式，它们可以通过感知信息素的浓度来判断路径之优劣，从而选择最优路径。如图1所示。

影响蚁群算法收敛的主要因素有蚂蚁数量m、信息素因子α、启发函数因子β、信息素挥发因子ρ、信息素常数Q、最大迭代次数t等。如表1所示。

1.4 蚁群算法的模型建立

蚁群算法主要通过模拟自然界蚂蚁在觅食过程中分泌的信息素来进行通信和协作。蚂蚁通过感知路径上的信息素浓度来选择下一步的移动方向。每个蚂蚁都会在移动过程中释放信息素，这些信息素会随时间推移逐渐挥发，也会因为蚂蚁经过而累积。这种机制使得较短的路径上信息素浓度逐渐累积，从而引导更多蚂蚁选择这些路径，最终找到最优路径[13]。

首先，定义关键变量：i和j为两个结点；bi（t）表示t时处于结点i的蚂蚁数；τij（t）为t时弧段（i，j）上的信息浓度；n表示结点集；m为整个蚁群中全部蚂蚁数量，；Γ=是在t时处于集合C中元素的信息素集合，设τij（0）=const，基本蚁群算法中蚂蚁寻求最优线路是利用有向图g=（C，L，Γ）实现的。

蚂蚁k（k=1，2，...，m）在爬行寻优过程中，利用先前蚂蚁残留的信息素浓度选择线路作为自己移动的方向。为了记忆蚂蚁是否已经过此结点，利用禁忌表tabuk记录蚂蚁爬行过的结点，禁忌表tabuk处于变化中 。蚂蚁的迭代过程，主要利用状态转移概率进行，那么t时蚂蚁k由一个结点选择另外一个结点的状态转移概率为：

其中，allowedk={C-tabuk}代表蚂蚁尚未走过的结点；α是代表蚂蚁所爬行轨迹重要程度的信息启发因子，主要反映了蚂蚁在路径选择过程中一定程度上参考了之前蚂蚁的残余信息素，而信息启发因子的取值大小即为其选择路径的强弱，α信息启发因子的取值大小即蚂蚁选择该路径的强度；β对期望启发因子而言，代表期望的重要程度，主要体现了蚂蚁进行路径选择对启发信息的重要程度，当然，当期望启发因子取值较大时，它就会向贪婪法则靠拢；ηij（t）为启发函数，ηij（t）=1/dij，式中dij代表每两个结点之间的长度或距离，对每个蚂蚁k，dij与ηij（t）呈负相关，dij越小，反而ηij（t）越大，相应地，状态发生转移的机率也就越高。很显然，该启发函数ηij（t）代表蚂蚁对从结点i转移到结点j的期望程度。

2 案例应用

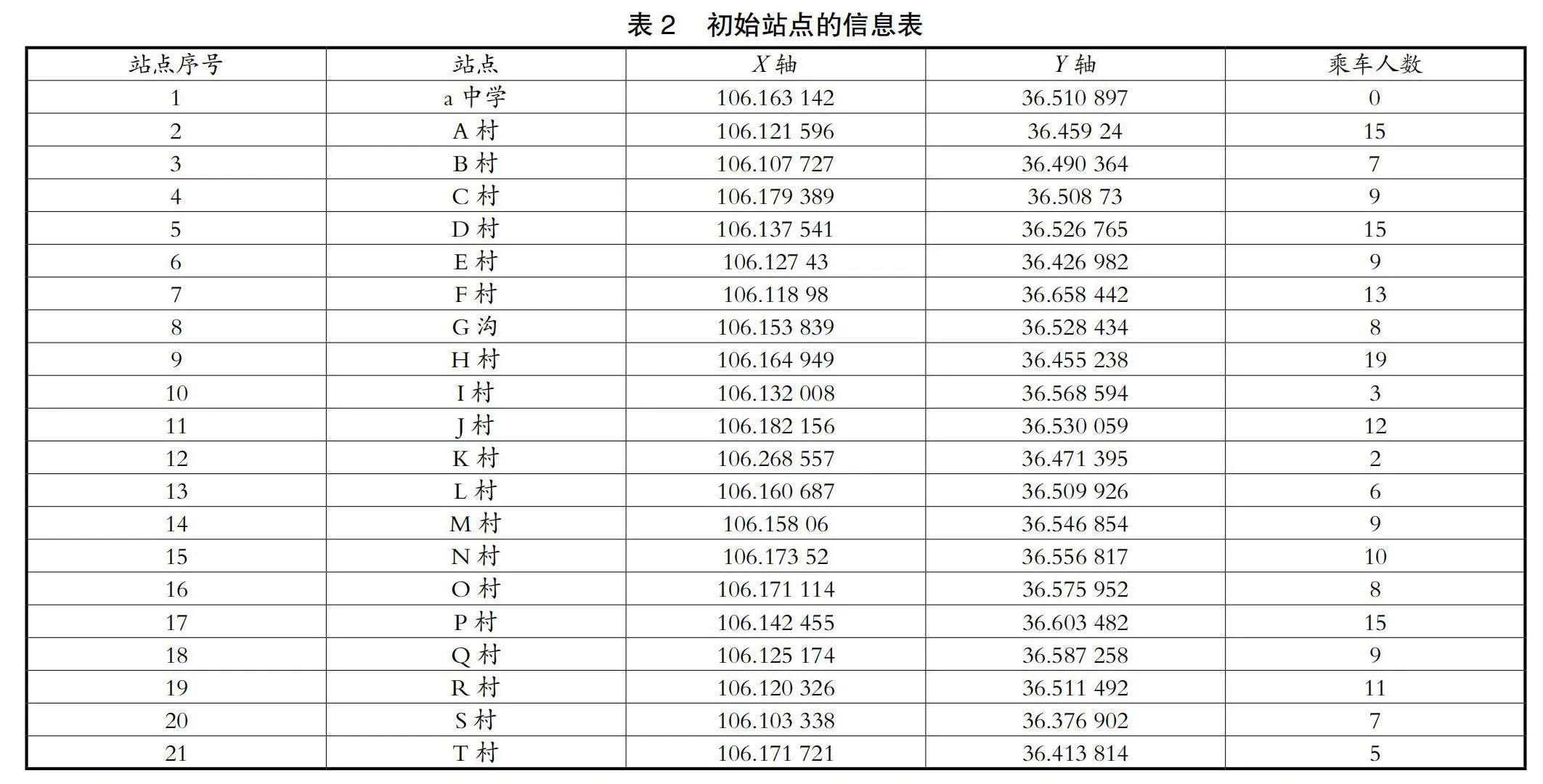
本文选定a中学作为研究对象，对该学校的学生进行统计，得出共有192名学生乘坐校车。现选用校车为可乘坐人数49人的车型。利用MATLAB软件对现有的21个站点进行路径规划，合理安排车辆数。

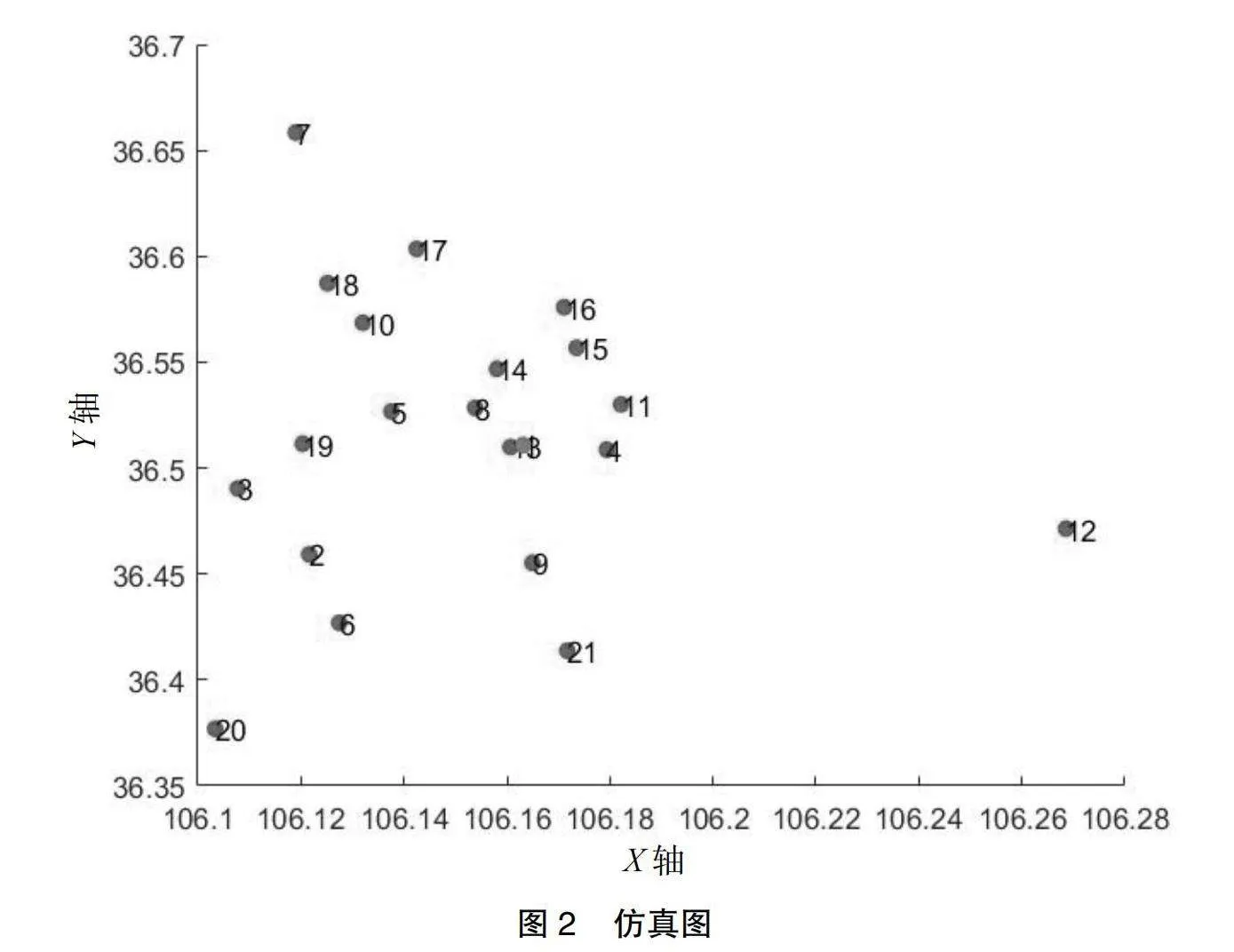
对所有学生的居住位置进行信息调查，将学生所在地划分为站点，并进行经纬度标注，这个位置就作为初始校车站点；然后统计在这个位置上车的学生人数。具体信息如表2所示。具体的实物图与MATLAB仿真图如图2所示。

由图2（站点的仿真图）可知，大部分站点靠近高速公路，道路条件良好，便于接送学生，只有K村距离公路较远。

3 结果分析

3.1 K-means算法的结果分析

K-means聚类分析算法具有简单且容易实现的优点，但需要事先设定类簇数量K，所以在利用该算法解决问题前需要依次设定K值，利用MATLAB进行仿真得到轮廓系数，并进行判断，得出K值为4，最终根据人数和距离得到路径。如图3和表3所示。

3.2 蚁群算法的结果分析

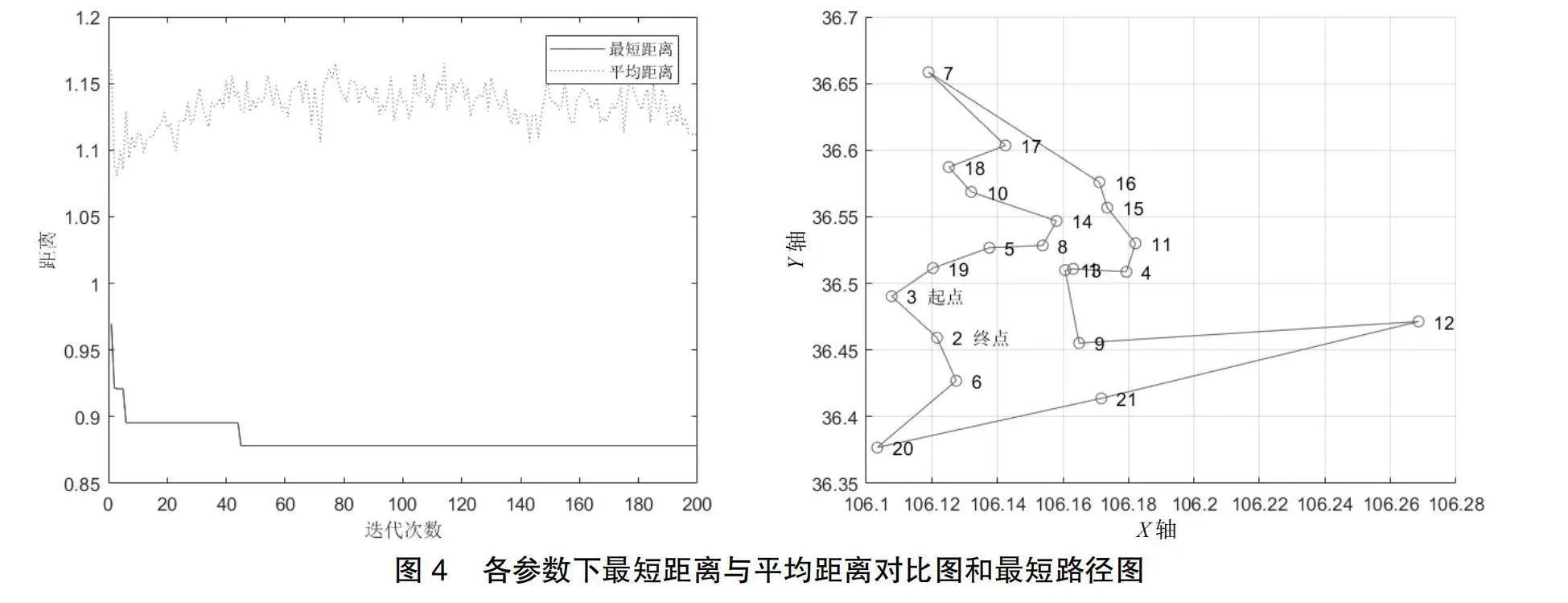
通过设置不同的参数，利用MATLAB软件得到，在不同参数数值下，各代最短距离与平均距离对比图，以及优化最短距离图得到各参数的取值如表4所示。各参数下经过迭代次数与距离以及最短路径图如图4所示。

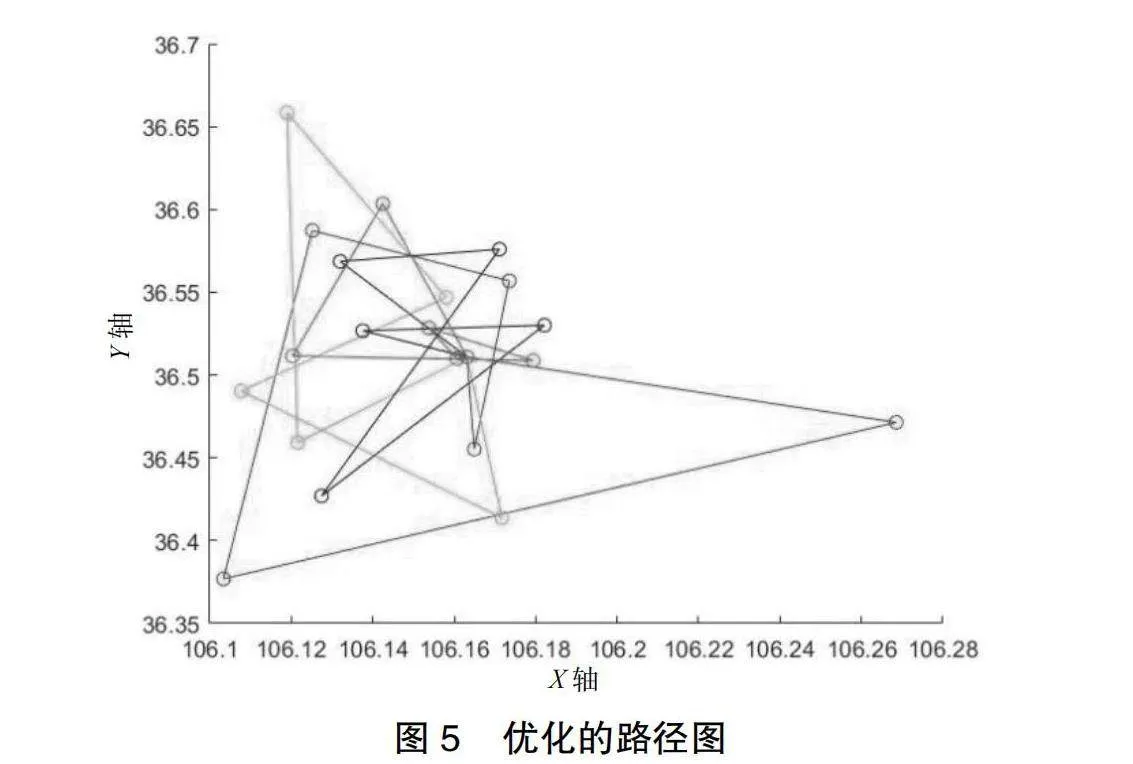
由图5的路径图得出该校学生乘坐校车的站点路线及人数如表5所示。

4 结 论

针对校车路径问题，讨论K-means聚类算法和蚁群算法这两种方法。通过对两种算法进行建模，针对调查实例学校的数据进行初始计算，采用MATLAB软件对数据进行仿真，对路径进行求解，最终得出每种算法下的路径数和车辆数，通过最后的仿真得知应用蚁群算法得出的路径较优，最终得出该学校需要购置车容量为49人的客车4辆。

参考文献：

[1] 任腾，罗天羽，李姝萱，等．面向冷链物流配送路径优化的知识型蚁群算法[J]．控制与决策，2022，37（3）：545-554.

[2] 柳伍生，李旺，周清，等．“无人机-车辆”配送路径优化模型与算法[J]．交通运输系统工程与信息，2021，21（6）：176-186.

[3] 张冬青，郭钊侠，张殷杰．考虑时空相关随机行驶时间的车辆路径问题模型与算法[J]．四川大学学报（自然科学版）， 2021，58（6）：181-189.

[4] 王勇，范举，刘永，等．基于客户信用度的物流配送车辆路径问题研究[J]．运筹与管理，2022，31（8）：77-84.

[5] 张春玲，张敬璇．物流配送中心选址研究[J]．华北理工大学学报（社会科学版），2021，21（5）：23-29.

[6] MENG Xiangxi， LYU Jianghua， MA Shilong．Applying improved K-means algorithm into official service vehicle networkingenvironment and research[J]．Soft Computing， 2020， 24（11）： 8355-8363.

[7] FADDA E， TIOTSOP L F， MANERBA D，et al．The stochastic multipath traveling salesman problem with dependent random travel costs[J]．Transportation Science，2020，54（5）：1372-1387.

[8] 周果，季彬，方晓平．多对多越库配送绿色车辆路径问题及算法研究[J]．铁道科学与工程学报，2022，19（8）：2202-2210.

[9] 胡小建，周琼，宋旭东，等．基于时间窗约束的多人多储位拣选路径优化模型及改进遗传算法应用研究[J]．计算机集成制 造系统，2022，28（11）：3354-3364.

[10] 薛德琴，张永强，王笑雨，等．基于聚类分析的协同配送中心选址研究[J]．物流工程与管理，2021，43（11）：56-58，40.

[11] 徐昊源，缪鸿志．基于K-means聚类的生鲜自提柜选址及配送方案优化[J]．物流技术，2022，41（11）：50-54.

[12] 唐慧玲，唐恒书，朱兴亮. 基于改进蚁群算法的低碳车辆路径问题研究[J]．中国管理科学，2021，29（7）：118-127.

[13] 韩孟宜，丁俊武，陈梦覃，等．基于混合遗传算法的应急物资配送路径优化[J]．科学技术与工程，2021，21（22）：9432-9439.

[14] 耿振余，陈治湘，黄路炜，等．软计算方法及其军事应用[M]．北京：国防工业出版社，2015.