基于灰色预测-ARIMA模型的石家庄货运周转量预测

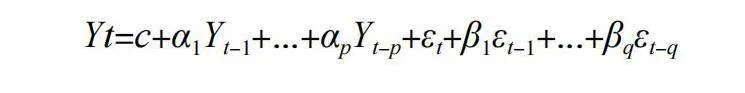
摘 要：石家庄素有“燕晋咽喉”之称，是全国重要的交通枢纽和商品物资集散地。随着物流运输业的迅猛发展，需要考虑石家庄的综合运输体系能否支撑未来区域经济的进一步发展，由此可见，石家庄市货运周转量的需求预测值得探讨研究。文章通过将灰色预测模型和ARIMA模型组合，利用多元回归方法确定组合模型权重，分别运用灰色预测、ARIMA模型及其组合模型三种模型对石家庄市的货运周转量进行预测分析。研究表明，相比单一模型，组合预测模型的预测精度更高，根据预测结果提出建议，对石家庄市物流行业的发展具有一定的参考价值。

关键词：组合预测；灰色预测；ARIMA模型；货运周转量

中图分类号：F326 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.002

Abstract： Shijiazhuang， known as "the transportaion hub of Beijing and Shanxi"， is an important transportation hub and commodity distribution center in China. With the rapid development of the logistics and transportation industry， whether the comprehensive transportation system in Shijiazhuang can support the further development of the future economy is need to be considered. It follows that it is worthy of exploration and research in predicting the demand for freight turnover in Shijiazhuang. This article combines the grey prediction model and the ARIMA model， and uses the multiple regression method to determine the weights of the combination model. Three models are used to predict and analyze the freight turnover in Shijiazhuang City， including the grey prediction model， the ARIMA model and the combination model of these two. The research shows that the combination prediction model has higher prediction accuracy than the single model. Suggestions are made according to the prediction results， which provide a certain reference for the development of the logistics industry in Shijiazhuang.

Key words： combination prediction; grey prediction; ARIMA model; freight turnover

收稿日期：2024-05-11

基金项目：河北省科技厅软科学智库项目“河北省科技成果转化政策体系实施效果评价及优化研究”（23557603D）；石家庄科技局软科学项目“石家庄市规上工业企业科技创新绩效评价及提升路径研究”（235790085A）

作者简介：崔艺豪（1999—），男，河北邢台人，河北地质大学管理学院硕士研究生，研究方向：物流工程与管理；李 婷（1968—），本文通信作者，女，河北石家庄人，河北地质大学管理学院，教授、正高级工程师，博士，研究方向：管理科学与工程。

引文格式：崔艺豪，朱子獒，李婷．基于灰色预测 -ARIMA 模型的石家庄货运周转量预测[J]．物流科技，2024，47（22）：8-11，18.

0 引 言

石家庄作为全国重要的交通枢纽，不仅承担了货物集散、通关服务的功能，而且推进了物流产业发展及其基础设施建设，促进了物流、资源要素的加速聚集，为京津冀构建“双循环”新发展格局提供了有力支撑。截至2024年7月，石家庄市已经实现了陆、海、空全线运行，出境口岸已达到7个，国际班列拓展至14条；全市已经建设了经济开发区、正定、鹿泉、栾城、高邑、新乐六大物流园区，集聚发展成效明显；全市在建亿元以上物流项目40个，极兔、京东等一批总部基地物流企业先后入驻，为打造千亿级现代商贸物流产业集群提供了强力支撑。市场繁荣的同时，石家庄市的货运周转量也在不断增长，物流供需是否会发生变化是需要相关部门考虑的问题，所以合理预测石家庄市未来货物量，夯实物流基础设施显得尤为重要。因此，构建精确的物流预测模型是很有必要的。

近年来，关于物流需求预测的研究已得到越来越多专家学者的关注。柳德才等（2023）构建了灰色预测法和指数平滑法的组合预测模型，预测并分析了江苏省的水产品物流需求量[1]。张乐等采用了GM（1，1）-MLP神经网络的组合预测法对物流总额进行预测，提高了预测精确度[2]。张雪（2020）运用灰色预测模型对河北省生鲜农产品冷链需求进行了预测[3]。丁天明等（2023）发现了经过粒子群算法改进后的灰色马尔可夫模型可以提高预测结果的准确性[4]。韩正超等（2020）认为物流行业的需求量是经济发展的相关产物，灰色预测和ARIMA是组合预测方法中的热点研究[5]。姜琳等（2024）采用了多元线性回归和灰色预测相结合的方式来进行需求预测[6]。

从已有研究来看[7-9]，学者们或将灰色预测模型与神经网络相结合，或使用经过算法改进的预测模型，或将灰色预测法与指数平滑法结合进行预测等，但将灰色预测模型与ARIMA模型结合的组合模型研究并不常见。本文通过灰色预测法、ARIMA模型及其组合模型进行对比分析，并引入多元线性回归确定其权重，旨在探讨更能提高预测精准度的模型，对于拓展预测方法种类和强化物流产业发展具有重要意义。

1 预测分析

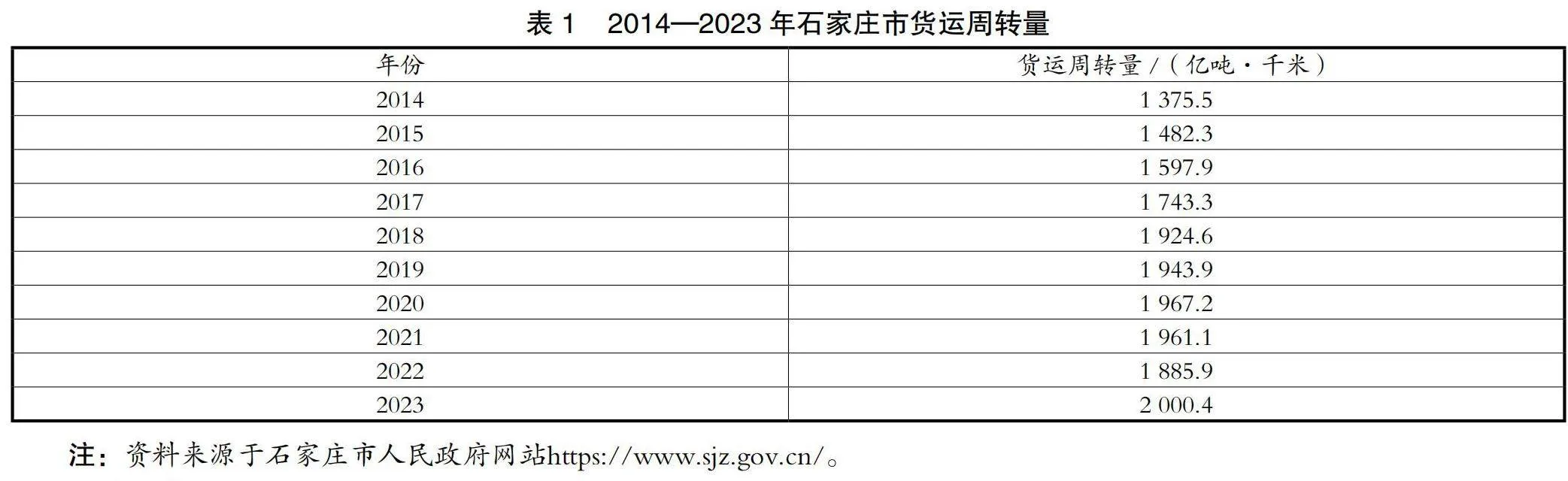
1.1 数据来源（见表1）

1.2 构建模型

1.2.1 构建灰色预测模型

一是数据检验。

确定原始数据序列：x（0）={x（0）（1），x（0）（2），...，x（0）（n）}，计算级比值。

二是进行累加。

构建新数列：x（1），x（1）={x（1）（1），x（1）（2），...，x（1）（n）}x（1）（n）=∑ki=1x（1）（i），i=1，2，3，...，n。

三是确定灰导方程：d（k）=x（0）（k）=x（1）（k）-x（1）（k-1）。

四是确定x（1）（k）的紧邻均值为z（1）（k）=，k=2，3，...，n。x（1）的紧邻均值数列为z（1）={z（1）（1），z（1）（2），...，z（1）（n）}。

五是确定灰微分方程。

结合上文二、三中公式，可得：x（0）（k）+az（1）（k）=b。发展系数a，灰色作用量b为模型构建输出值。代入k的具体值结果如下。

令Y=（x（0）（2），x（0）（3），...，x（0）（n））T，则Y=Bu。

六是白化方程。

上式，x（0）（k）+az（1）（k）=b，x（0）（k）为k的连续函数，变化方程如下。

七是模型求解。

x（0）（k+1）=x（1）（k+1）-x（1）（k），k=1，2，3，...，n-1

1.2.2 构建ARIMA模型

ARIMA方程式为如下。

Yt=c+α1Yt-1+...+αpYt-p+εt+β1εt-1+...+βqεt-q

具体过程如下。

数据预处理：对时间序列数据进行观察和检查，确保数据没有缺失或异常。如果有必要，可以进行平滑处理、差分运算或其他预处理操作。

确定模型阶数：通过观察自相关图（ACF）和偏自相关图（PACF）确定ARIMA模型的阶数。ACF图可以帮助确定移动平均阶数，而PACF图则有助于确定自回归阶数。此外，还可以利用信息准则定阶法，如AIC和BIC，来辅助确定模型阶数。

参数估计：使用最大似然估计或其他方法来估计ARIMA模型的参数。通过将残差平方和最小化来寻找最佳参数值。

模型检验：模型的检验主要关注模型的残差序列是否符合白噪声的假设。如果残差序列不是白噪声序列，则需要重新从模型识别和定阶步骤开始对模型进行重新拟合。

1.2.3 构建组合预测模型

组合上述两种模型，设xi为第i年的货物周转量，xij为第i年第j种方法的货物周转量预测值，eij=||×100%为第i年第j种方法预测值的相对误差，ωj为第j种方法的权重，为组合预测值，模型公式如下。

minE=∑nm==11×100% s.t.∑ji=1ωj=1，ωj≥0

2 石家庄市货运周转量需求预测

该组合模型设xi为第i年的实际货物周转量，为第i年的货运周转预测值，i为第i年的组合预测值，组合模型方程为ω1GM+ω2ARIMA，约束条件为ω1+ω2=1。组合权重参数通过多元线性回归进行独立性权重计算，分别用GM（1，1）模型、ARIMA模型及组合模型对石家庄市货运周转量进行预测分析。

2.1 GM（1，1）预测

进行级比检验，检验通过表示该序列适合构建灰色模型，若不通过则转换序列，直到新序列通过级比检验。通过SPSS分析可得，初始序列全部级比值均位于（0.834，1.199）区间，计算得出相关指标，发展系数a为-0.029 8，灰色作用量b为1 558.194 6，后验差比c为0.184 9，小误差概率p为0.9。根据后验差比和小误差概率值，可知模型精度极好，可以构建灰色模型。拟合结果见表2。

表2中，相对误差越小，拟合效果越好。表中相对误差小于20%，表明拟合良好。计算该模型的平均相对误差为4.330%。

2.2 ARIMA模型预测

第一步：检验ADF。根据t值分析其是否可以显著性拒绝序列不平稳的假设（p<0.05）。

从表3可得，***代表1%的显著性水平。

该时间序列数据ADF检验的t统计量为-2.235，p值为0.194，1%、5%、10%的临界值分别为-4.473、-3.290、-2.772。p=0.194＞0.1，不能拒绝原假设，序列不平稳。对序列进行一阶差分再检验。一阶差分后检验结果显示p=0.000***＜0.1，此时拒绝原假设，序列平稳。

第二步：检验模型，首先ARIMA模型要求模型残差为白噪声，通过Q统计量检验进行白噪声检验（原假设：残差是白噪声）；然后Q6用于检验残差前6阶自相关系数是否满足白噪声，通常其对应p值大于0.1，说明满足白噪声检验（反之说明不是白噪声）；最后如果拒绝白噪声假设（p＜0.05），意味着模型拟合不佳，反之表示模型可以使用。

根据Q统计量结果，Q6的p值大于0.1，则在0.1的显著性水平下不能拒绝原假设，模型的残差是白噪声，模型满足要求。其模型公式为：y（t）=385.442+1.333 *y（t-1）-0.553 *y（t-2）。

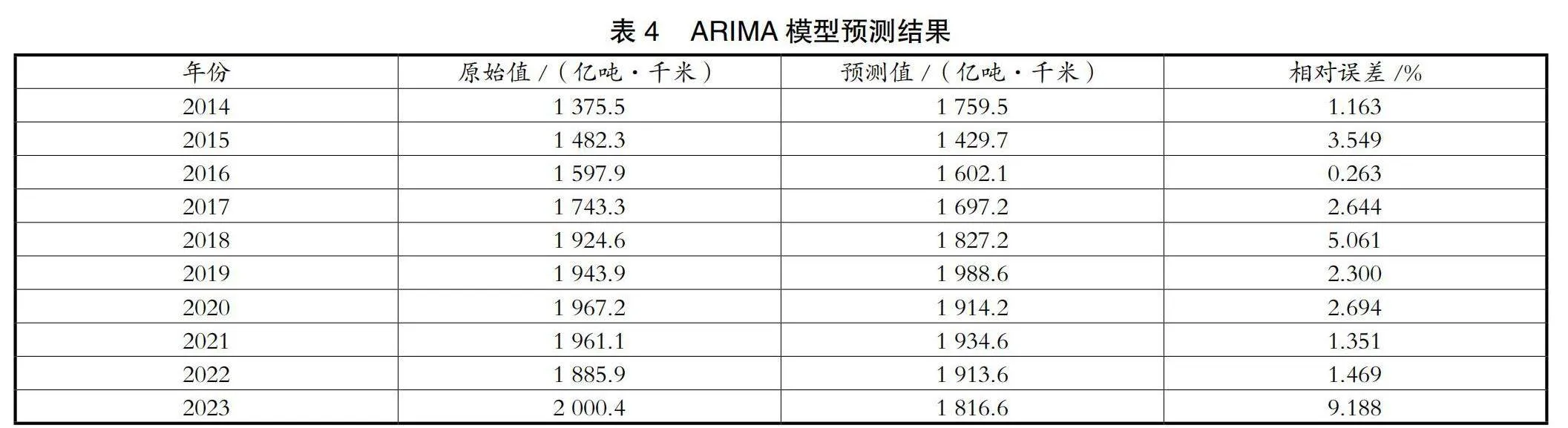
预测结果见表4。

ARIMA模型平均相对误差为2.968%。

2.3 组合预测

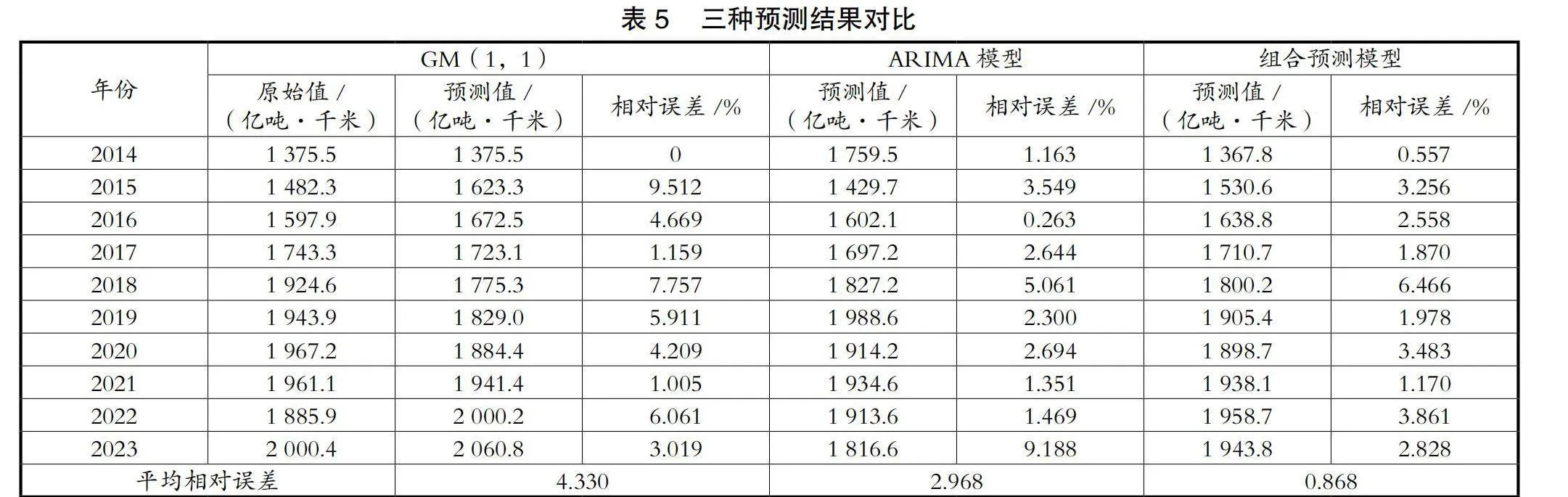
利用多元回归方法，进行权重计算，得出灰色预测模型的权重参数为0.521，ARIMA模型的权重参数为0.479，构建组合模型为i=0.521GM+0.479ARIMA。三种预测结果如表5所示。

由表5可知，组合模型的预测平均相对误差为0.868%，其预测精确度远超单一使用灰色预测模型和ARIMA模型的精确度。现进行三种模型的预测（见表6）。

3 结论与建议

本文采集了石家庄市国民经济和社会发展统计指标（货运周转量），采用灰色预测法和ARIMA模型及其组合模型分别对石家庄市的货运周转量进行了预测，研究结果显示，组合预测模型可以提高预测数据的精准度，为相关部门提供更准确的参考信息。根据组合模型的预测结果，石家庄市未来7年的货运周转量将呈持续稳步上升的趋势。

根据预测结果，现提出以下几点建议：首先，石家庄市在着重打造物流强市的基础上，加快建设大载体、畅通大网络、搭建大平台、培育大企业，提升现代化、国际化、智慧化、绿色化水平，打造优质高效现代物流体系。其次，制定政策支持物流企业做大做强，可适当奖励企业补贴。进一步优化产业布局，升级现代化商贸物流体系，鼓励物流企业有序向三环外疏解，在三环外新建物流园区。再次，促使物流企业进行全链条模式升级，加快其从单一环节盈利模式转向综合竞争，强化其供应链一体化的能力，逐步由低附加值服务转为高附加值服务，呈现新的增长趋势。最后，充分发挥智能技术，构建数字共享平台，提高物流智能化、自动化水平，增强信息监管，提高实时追踪物流信息的能力。

参考文献：

[1] 柳德才，周志杰．基于组合预测模型的水产品冷链物流需求预测研究——以江苏省为例[J]．物流工程与管理，2023，45（10）：4-8.

[2] 张乐，汪传旭．基于GM（1，1）-MLP神经网络组合模型的物流总额预测[J]．上海海事大学学报，2018，39（4）：58-62.

[3] 张雪．基于GM（1，1）模型的河北省冷链物流需求预测[J]．价值工程，2020，39（6）：124-126.

[4] 丁天明，潘宁，杜柏松，等．基于改进灰色马尔可夫的港口货物吞吐量预测研究[J]．重庆交通大学学报（自然科学版），2023， 42（9）：130-136.

[5] 韩正超，张有云，黄文霞．基于BP神经网络的济南市物流需求预测[J]．软件，2020，41（3）：149-152，241.

[6] 姜琳，盛帅铎．基于GM（1，1）模型的河南省物流需求组合预测[J]．物流科技，2024，47（4）：27-33，61.

[7] 翟珊珊，段婕．组合权重确定方法的仿真对比分析[J]．统计与决策，2015（24）：83-85.

[8] 邹荣妹，兰国辉，杨霞．基于组合预测的港口货物吞吐量分析——以长三角港口群为例[J]．廊坊师范学院学报（自然科学 版），2024，24（1）：92-99.

[9] 程元栋，喻可欣，李先洋．基于加权马尔科夫-ARIMA修正模型的区域物流需求预测[J]．山东交通学院学报，2023，31（3）：22-28.