Perfect Pick系统订单拣选策略优化研究

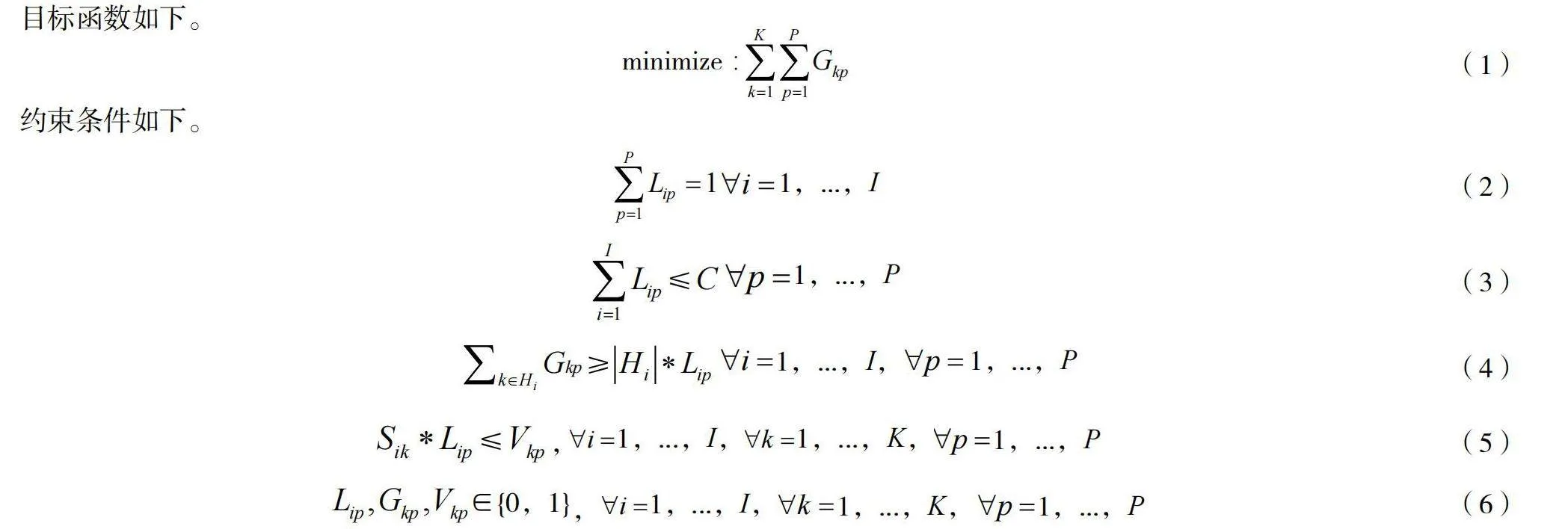
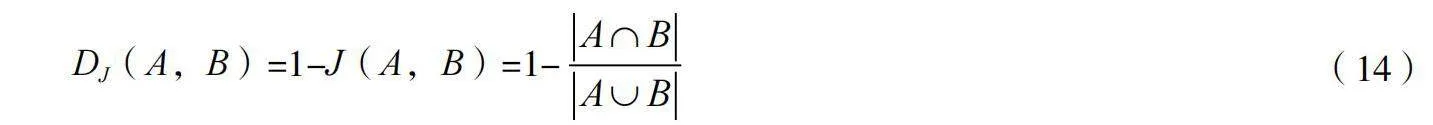
摘 要：作为电商仓库作业中耗时最长、成本最高的环节，订单拣选的作业效率一直是仓库管理中的关键问题。文章针对拣选策略选择问题，选择Perfect Pick系统的电商仓库作为背景，对单个拣选台进行研究，提出订单分批和订单排序两种拣选策略并进行对比分析；以货箱搬运次数最少为目标，分别构建订单分批与订单排序两种拣选策略的整数规划模型，并设计贪婪算法进行求解。通过数值实验验证，订单排序策略在所有订单规模中均优于订单分批策略，根据仓库的订单规模，合理设置拣选台最大容量并选择合理的拣选策略，能够更好地提高拣选效率、优化仓库作业环节。

关键词：Perfect Pick系统；订单拣选；订单分批；订单排序

中图分类号：F252 文献标志码：A DOI：10.13714/j.cnki.1002-3100.2024.22.001

Abstract： Order picking is the longest and the most expensive part in the e-commerce warehouse operation， and its operation efficiency has always been a key issue in the warehouse. Addressing the selection of picking strategies， taking the e-commerce warehouse equipped with the Perfect Pick system as the background， this paper conducts a research on a single picking platform， provides two picking strategies， including order batching and order sequencing， and compares and analyzes them. In order to minimize the number of container handling， integer programming models of order batching and order sequencing are constructed respectively， and the greedy algorithm is designed to solve them. Through the numerical experiment， it is verified that the order sequencing strategy is superior to the order batching strategy in all order sizes. Setting the maximum capacity of the picking table reasonably according to the order size of the warehouse and choosing a reasonable picking strategy can better improve the picking efficiency and optimize the warehouse operation.

Key words： Perfect Pick system; order picking; order batching; order sequencing

收稿日期：2024-05-11

基金项目：教育部人文社会科学项目（19YJA630054）；武汉科技大学资助项目智慧物流数字运营平台开发研究（2022H20537）

作者简介：马云峰（1972—），男，吉林蛟河人，武汉科技大学管理学院，武汉科技大学服务科学与工程研究中心，教授，博士，研究方向：物流系统规划、管理定量分析等；邓 力（1999—），男，湖北黄冈人，武汉科技大学管理学院硕士研究生，研究方向：智能仓储、物流系统规划；余家祥（1991—），男，湖北武汉人，湖北港口集团有限公司，武汉现代物流研究院有限公司，高级物流师，硕士，研究方向：物流系统规划。

引文格式：马云峰，邓力，余佳祥．Perfect Pick 系统订单拣选策略优化研究[J]．物流科技，2024，47（22）：1-7.

0 引 言

近年来，我国社会经济快速发展，互联网技术日新月异，电子商务作为一种新型经营模式正在不断兴起且迅猛发展，电商企业的客户越来越多，意味着电商企业要处理的订单也越来越多，拣选环节已成为仓库研究的重点环节。面对大量订单拣选任务，传统的“人到货”拣选方式需要大量人工，拣选时间长、效率低[1]；而“货到人”拣选方式是通过搬运设备运送货物的，这种方式减少了人工需求量，大大缩减了拣选时间。

货到人拣选系统种类繁多，每种系统都有其独特的优势和特定的适用场景[2]。对于那些存储了大量重型货物的仓库而言，部署堆垛机和托盘系统可能更适宜，因为它们能够有效处理重物的存储和搬运；而对于需要迅速处理大量小件商品的仓库，采用传送带和四向穿梭车系统则会更加高效，因为这类系统擅长快速且准确地移动和分拣小件物品[3]。

本文研究的Perfect Pick系统是一种独特的机器人货到人订单拣选技术，旨在简化订单履行方式。订单拣选是订单履行中的重要部分，张学朋（2022）综合订单分批、拣选路径和人员数量设计了种子算法来求解[4]。冯爱兰等（2020）考虑了流利式货架系统，以最小化订单在缓存区的滞留时间和拣选员的操作等待时间为目标，设计了遗传算法进行求解[5]。李珍萍等（2021）基于聚类思想，构建了以货架搬运次数最少为目标的订单分批模型[6]。郝梦君（2023）针对多个拣选台，研究订单分配与排序问题，在基本变领域搜索算法的基础上设计了求解模型的MVNS算法进行问题求解[7]。何昕杰等（2021）考虑四向穿梭车货到人拣选系统中四向穿梭车与提升机的作业时长，采用遗传算法求解订单的出库顺序[8]。

本文以货箱搬运次数最少为优化目标，分别构建了订单分批与订单排序两种拣选策略的整数规划模型，将问题分解为订单选择与货箱选择两个评估子问题，并设计贪婪算法进行求解。

1 问题描述

Perfect Pick系统中商品的存储单元为移动式货箱，货箱中可以放置分隔板以便储存不同的商品。本文研究在其中单拣选台的订单拣选环节，如何对订单进行合理分配，才能使总搬箱次数最小。

1.1 订单分批

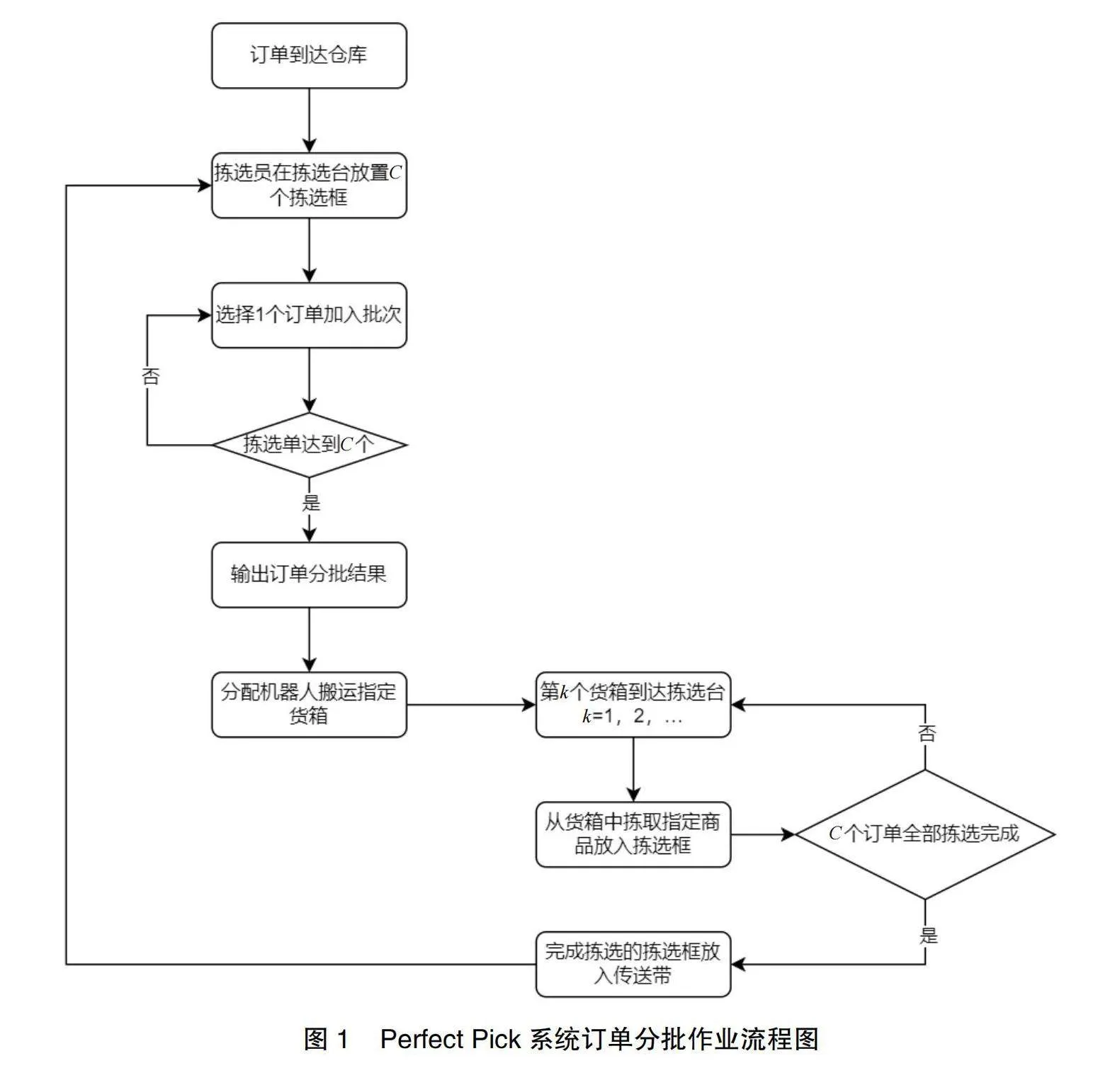
在每一批次开始时，系统都会从订单池中选取C个订单，并将其指派到拣选台；随后，系统会调度机器人将货箱搬运到拣选台；一旦货箱到达，拣选员便会根据货箱中的商品信息，将相应商品拣取出来，并放入对应的拣选框中；这个过程会不断重复，直到C个订单的所有商品都被完全拣取完毕，在一批订单拣选完成之后再进行下一批次的拣选。基本作业流程如图1所示。

1.2 订单排序

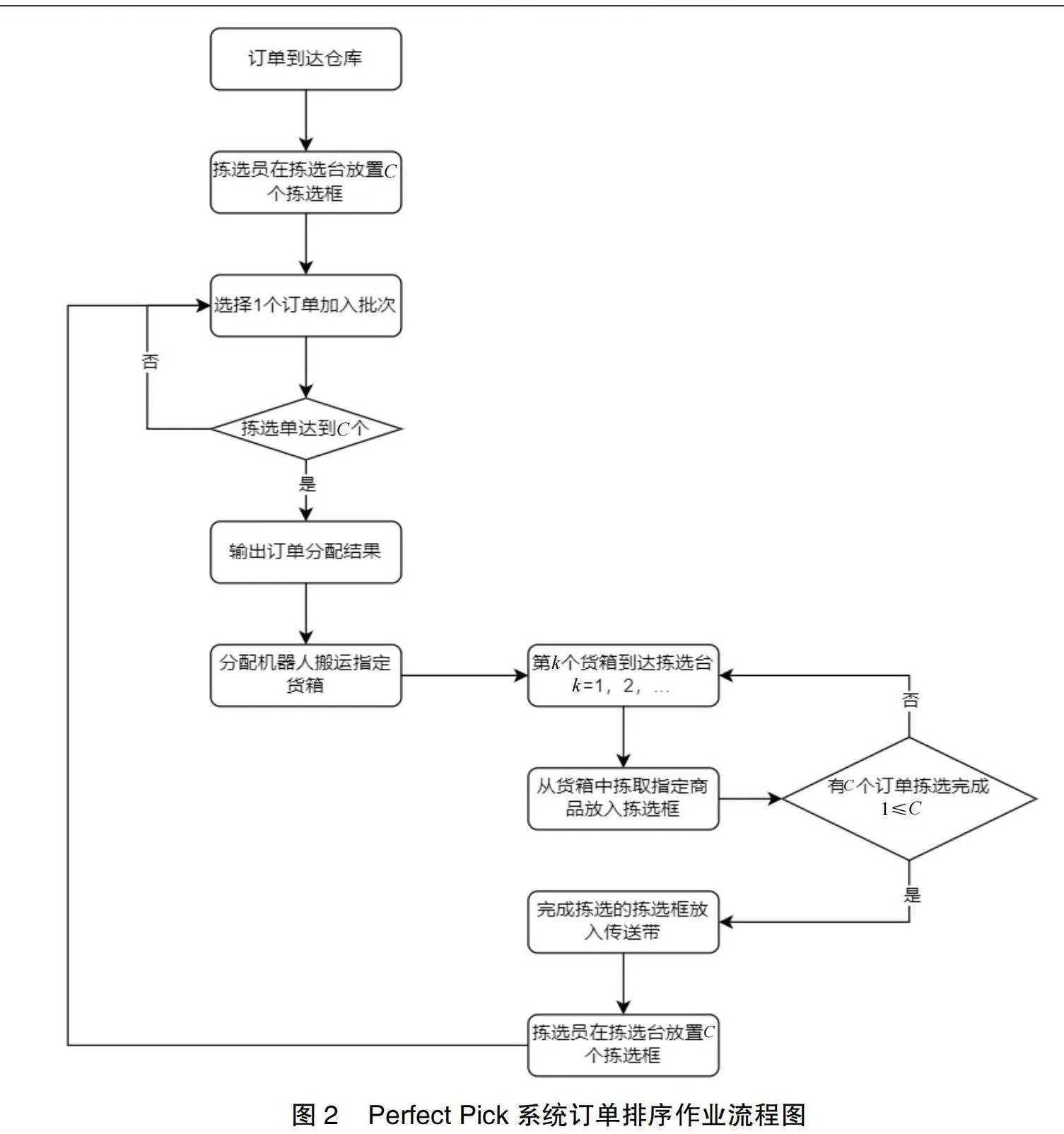
在订单排序问题中，拣选员会不断执行拣货任务，直到拣选台上其中一个订单的商品全部被拣选；一旦某个订单的所有商品都完成了拣选工作，拣选员就会将该订单的拣选框放到一旁的传送带上，紧接着在同一位置放置一个全新的拣选框；此时，系统会指派一个新的订单到拣选台，空的拣选框就代表着新的待拣选订单；重复上述过程，直到所有订单的商品都拣选完毕。基本作业流程如图2所示。

1.3 相关假设与设定

为简化问题，在不影响所研究问题本质的前提下，作出以下假设。

一是拣选区货箱的存储数据已知，不存在缺货情况，且不存在紧急插单情况。

二是货箱的位置是固定的，即机器人搬运货箱完成拣选作业后，回库时会回到货架的原位置。

三是在处理订单之前预先确定要从中拣取每个商品的货箱。

四是不考虑拣选台之间的影响，每个订单只能划分到一个批次，且不可分割。

五是不考虑拣货员从货箱中检索商品的时间差别。

六是移动机器人的移动、充电或堵塞等任何情况都不会对任务的完成情况产生影响，且数量足够。

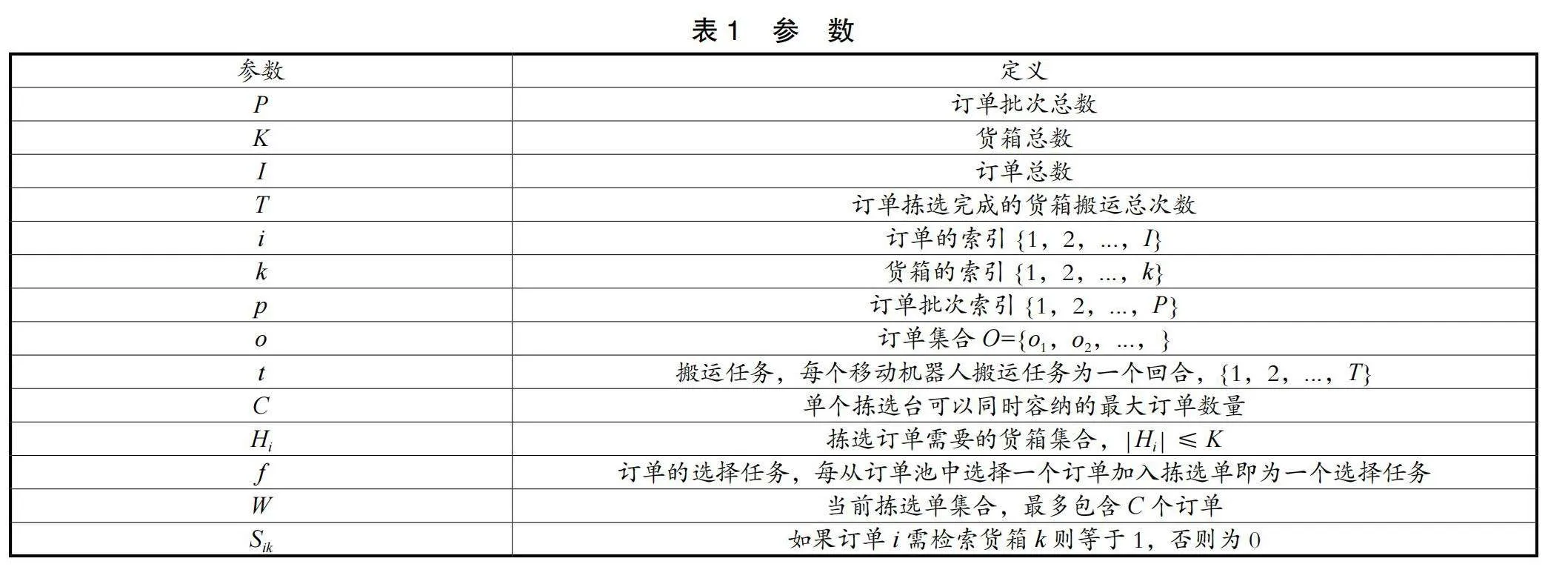
模型参数及变量定义如表1、表2所示。

2 模型建立

2.1 订单分批模型

目标函数如下。

约束条件如下。

其中，式（2）确保每个订单oi都会被分配到订单批次中；式（3）确保每个批次的订单数量都不超过一个拣选台的最大订单容量限制；式（4）确保一个订单如果被分配到某个批次，则该批次必须包含所有必要的拣选货箱以满足该订单的商品需求；式（5）保持和的一致性，确保每个批次包含其所有订单所需的所有拣选货箱；式（6）为决策变量取值约束。

2.2 订单排序模型

目标函数如下。

约束条件如下。

其中，式（7）是订单分批模型的目标函数，即最少货箱搬运总次数；式（8）确保每个搬运任务仅搬运一个货箱；式（9）确保任意搬运任务t中，拣选台上的订单总数不能超过其最大处理能力C；式（10）确保订单在拣选台上的处理是连续的，避免处理中断；式（11）表示拣选每个订单oi所需的所有货箱k至少在一次搬运任务中被拣选，确保订单完整性；式（12）为决策变量取值约束。

3 算法设计

3.1 订单和货箱选择评估方法设计

3.1.1 订单选择评估方法

订单选择是指在订单池中选择订单加入拣选单的过程，本文分为两个步骤。

首先，每个订单批次中第一个订单的选择，这里提出使用综合评分法进行评估。

综合评分（Score）由两部分组成：多样性得分（SC）和共享度得分（SD）。这两部分通过一个参数α加权融合，以计算每个订单的总评分。多样性评分是基于订单中不同货箱种类的数量，共享度得分则是基于订单中所有货箱在所有订单中出现次数的总和。

其中，SC（Oi）=|Oi|，|Oi|表示订单i中货箱的种类数。

SD（Oi）=∑*k∈OiFreq（k），Freq（k）表示货箱k在所有订单中出现的次数。

α是一个权重系数，用于平衡多样性和共享度的影响，范围是0～1。

这个公式允许评估每个订单的“评分”，通过考虑订单的货箱多样性以及这些货箱与其他订单的共享程度，选择综合评分最高的订单作为第一个订单。

其次，后续订单的选择通过计算订单相似度的方法进行。本文采用杰卡德距离来衡量订单相似度。

杰卡德距离如下。

式中，|A∩B|表示集合A和B交集元素的数量，|A∪B|则表示集合A和B并集元素的数量。杰卡德距离在区间[0，1]内取值，即杰卡德距离越小，订单相似度越大。选择订单相似度大的订单加入拣选单，可以提高每个货箱到达拣选台时所能服务的平均订单数。

3.1.2 货箱选择评估方法

货箱选择是指在完成订单选择任务，组成拣选单之后，安排移动机器人搬运货箱的过程。在这里，我们选定每个拣选单中的货箱种类，计算其与订单池中未参与拣选的所有订单的货箱重合数F（k）来作为货箱匹配度，具体计算方式如下。

其中，k表示拣选单中的某一个货箱种类；E为拣选单中所有订单的货箱集合；Or代表订单池中所有未参与拣选的订单集合；F（k）表示货箱k与Or中所有订单的货箱重合数；count（k，Oi）是货箱k在订单Or中的出现次数。

基于这个计算，选择下一个要搬运的货箱k*的规则可以表示如下。

该公式的含义为从拣选单所有订单的货箱集合E中选择一个货箱k*，使其在未参与拣选的订单集合Or中的重合数量最小。当F（k）没有差异时，优先拣选快完成订单的所需货箱。该策略旨在优先搬运在未来订单中出现较少的货箱，以期减少对后续拣选过程的干扰，提升整体拣选效率。

3.2 订单分批问题算法设计

采用贪婪算法完成订单分批问题的求解，具体步骤如下。

Step0：数据输入，输入待拣选订单集合O，满足需求的货箱数量K。拣选台可同时进行拣选作业的订单数量为C。

Step1：计算订单池中订单的综合评分，选择综合评分最高的订单加入拣选单。

Step2：计算订单的杰卡德距离，选择数值最小的订单加入拣选单。该过程将持续进行，直到拣选单中订单的数量达到C。

Step3：计算该批次订单所需的货箱总和。该批次订单每需要一个不同的货箱就计为搬运次数加一，计算完毕后删除拣选单，即该批次订单拣选完毕。

Step4：开始新的订单批次选择，重复计算综合评分与订单杰卡德距离的订单环节。

Step5：拣选单完成，进入拣选环节。重复Step3。

Step6：重复订单分配和拣选环节，直到订单池中所有订单拣选完毕。过程中若订单池的剩余订单数小于C，则将剩余订单组成最后一个订单批次，进行拣选。

Step7：算法结束，输出订单分批结果及货箱搬运总次数。

3.3 订单排序问题算法设计

采用贪婪算法求解订单排序问题，具体步骤如下。

Step0—Step2：与订单分批相同。

Step3：对货箱与拣选单进行匹配度计算，从中选出最合适的货箱作为本次的拣选货箱，随后将选中的货箱加入货箱的搬运任务列表中进行排序，并删除拣选单中对应的待拣货箱，表示该货箱的拣选工作已经完成，相应地将搬运次数增加一次。这个过程会不断重复，直至拣选单中的所有订单均完成拣选任务。

Step4：将已完成的订单从拣选单中删除，开始新的订单选择。重复计算过程，将新的订单加入拣选单，直到拣选单的订单数量达到拣选单容量C。

Step5：拣选单完成，进入拣选环节。重复Step3。

Step6：重复订单分配和拣选环节，直到所有订单均已加入过拣选单中进行拣选，便停止订单分配，继续当前拣选单的拣选任务，直到所有待拣货箱拣选完毕。

Step7：算法结束，输出订单排序结果、货箱的排序列表以及货箱搬运总次数。

4 实验分析

运用Python软件进行数值实验，从而验证订单分批模型和订单排序模型及相关算法的有效性、可行性及其优化效果。

4.1 实验参数设置

随机数据生成逻辑如下。

货箱信息生成：通过随机分配算法，将X种商品随机分配到Y个货箱中。每个货箱根据仓库的实际存储策略存储1～6种商品。

订单生成：基于I张订单的需求，随机生成拣选每个订单的所需货箱数量及种类，以模拟电商订单的波动性和多样性。

考虑到订单直接对应货箱的情况，每个订单包含一个货箱集合，拣选台根据订单所需拣选货箱直接进行商品拣选。实验还考虑了拣选台可同时处理的订单数，即拣选台最大容量C对拣选效率的影响。拣选台容量的变化范围设定为12～48，包含多个测试点（12、16、20、24、28、32、36、40、44、48）。

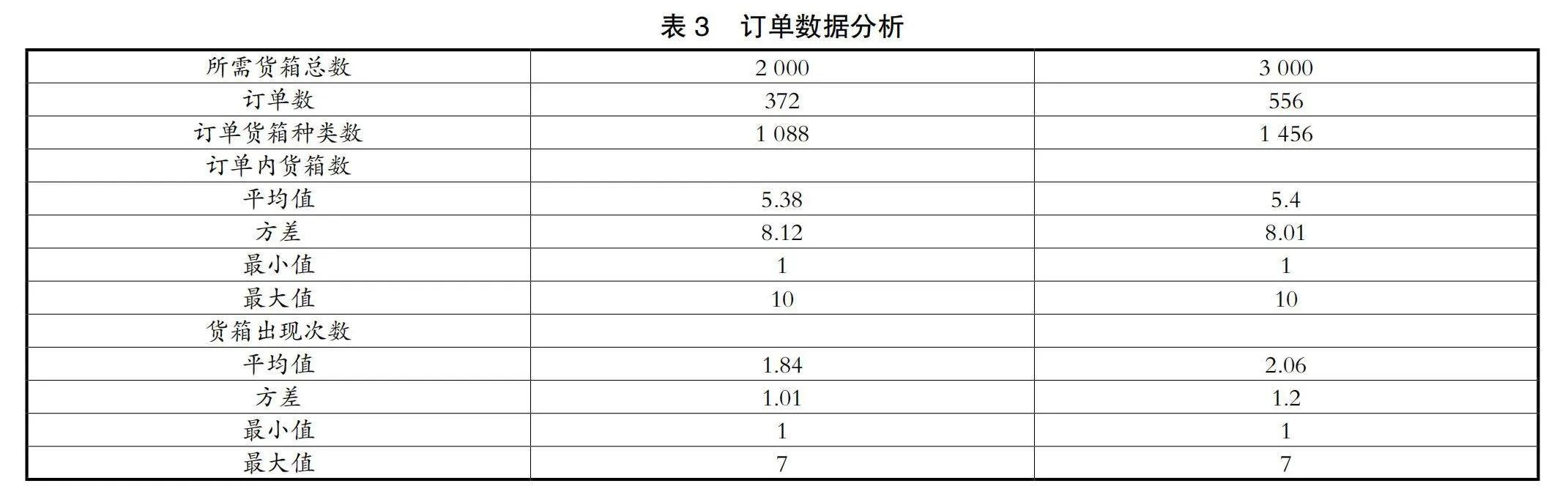
由于电商订单具有波动性，选取不同的订单商品总数，即不同的订单池所需货箱数量，来反映不同的拣选台工作量。本文设定了两个不同订单的所需货箱规模：K=2 000、K=3 000。为了清晰说明算法效果，实验引入随机分批策略的结果作为对照。具体订单数据分析见表3。

4.2 结果分析

4.2.1 实验结果

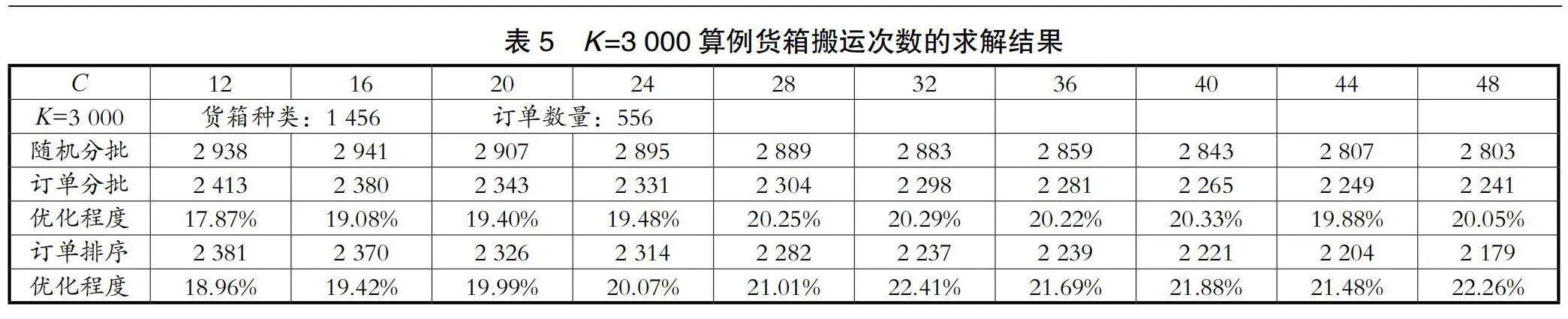
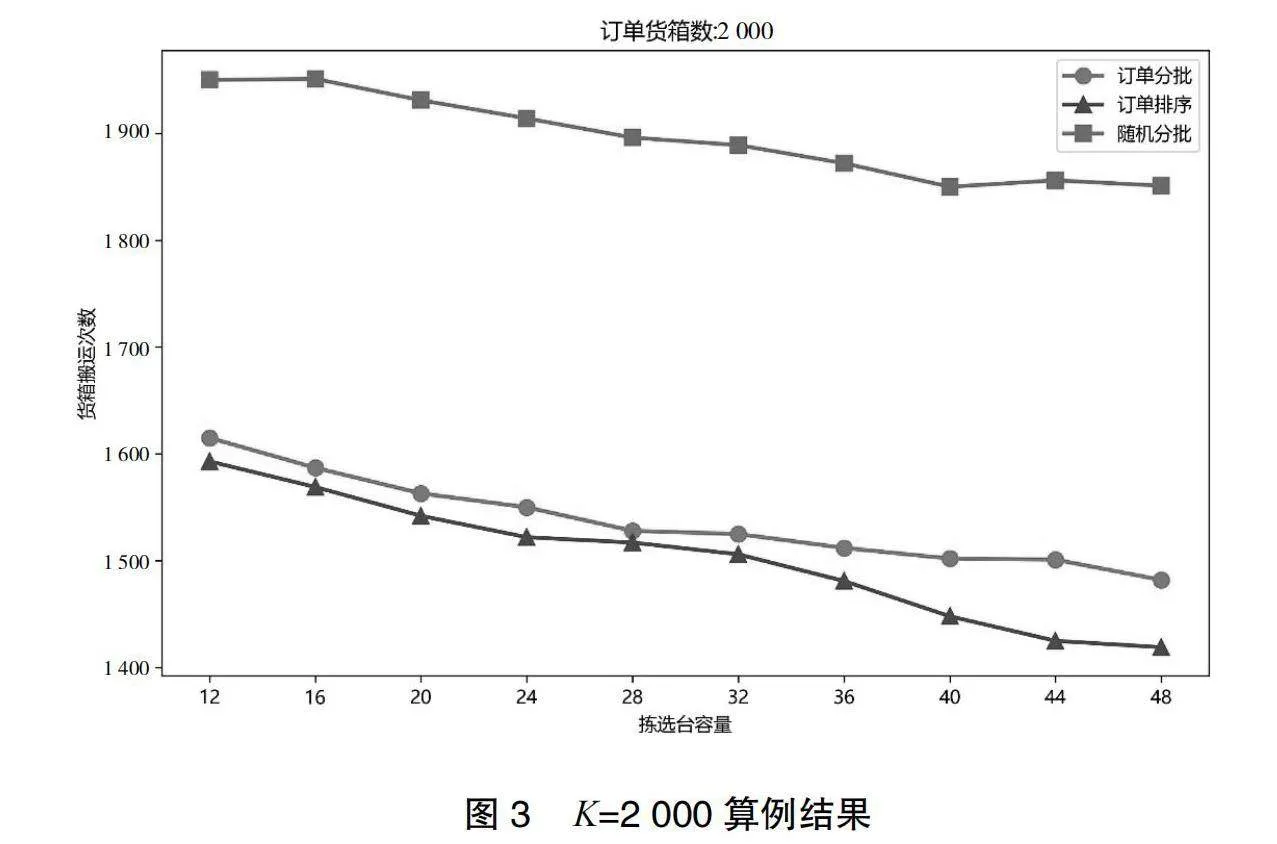
实验结果被记录在表4至表5中，并通过图3至图4直观展示了在不同的拣选台容量设置下，三种拣选策略对应的货箱搬运次数。

当订单货箱总数为2 000时，随机分批拣选次数明显多于其他两种策略，从1 953减少到了1 851，订单分批和订单排序策略则显示出了更明显的效率提升，拣选次数分别从1 615减少到1 482，从1 593减少到1 419。在此条件下，排序优化程度达到了最高值23.34%，高于分批优化程度的最高值19.94%。

对于货箱总数为3 000的算例，结果数据同样显示随着拣选台容量的增加，所有策略的拣选次数均有所减少，其中订单排序策略的优化效果最为显著。在货箱总数为3 000时，排序优化程度的最高值达到了22.26%。

4.2.2 效果分析与参数影响

4.2.2.1 不同拣选策略结果对比

订单排序策略在所有给定的货箱总数设置中均表现出了最佳优化效率，尤其是在拣选台容量较大时，其效率优势更为显著。当订单货箱总数分别为2 000、3 000时，与随机分批相比，本文所提出的订单排序策略的优化程度最大分别达到了23.34%、22.26%。这表明在实际的仓库管理中，采用基于数据和算法优化的订单排序策略，能够显著提升拣选效率，减少操作时间。

4.2.2.2 拣选台最大容量的影响

实验数据清晰表明拣选台容量增加对于减少货箱搬运次数和提高优化率具有显著的正面影响，这种影响在订单分批策略和订单排序策略中尤为突出，表明通过合理优化拣选台的配置可以有效提高仓库的作业效率。

5 结 论

本文以电商仓库应用Perfect Pick系统为研究背景，对比分析了仓库订单在分批策略与排序策略下的拣选流程及工作效率。针对文中所提及的问题，以货箱搬运次数最少化为优化目标，分别构建了相应的整数规划模型。本文将拣选问题拆分为两个子问题，并设计了相应的评估策略，采用贪婪算法进行求解。对比分析发现，以本文所提出的评估策略实现订单排序要优于订单分批，相比于订单随机分批，货箱总搬运次数的优化程度可达18％～23％，且对拣选台容量变化的敏感度最高。在未来的工作中，可以考虑对多个拣选台的问题进行分析，进一步研究订单分配至拣选台的优化策略以及拣选台之间互相占用货箱的情况。

参考文献：

[1] 高翔，李爽爽，谢正忠．电子商务环境下物流管理发展策略研究[J]．物流工程与管理，2022，44（1）：91-93.

[2] 王姗姗，张纪会. “货到人”拣选系统订单分批优化[J]．复杂系统与复杂性科学，2022，19（3）：74-80.

[3] 刘刚，王艳艳，黄珂，等．穿梭车自动存取系统任务调度算法适配性研究[J]．计算机集成制造系统，2022，28（5）：1435-1448.

[4] 张学朋．A电商公司Y仓库订单拣选作业优化[D]．石家庄：河北科技大学，2022.

[5] 冯爱兰，王晨西，孔继利．改进遗传算法求解订单分批优化模型[J]．计算机工程与应用，2020，56（8）：261-269.

[6] 李珍萍，田宇璇，卜晓奇，等．无人仓系统订单分批问题及K-max聚类算法[J]．计算机集成制造系统，2021，27（5）：1506-1517.

[7] 郝梦君．基于AMR的货到人拣选系统的订单分配与排序优化问题研究[D]．北京：北京交通大学，2023.

[8] 何昕杰，周少武，张红强，等．基于改进遗传算法的四向穿梭车系统订单排序优化[J]．系统仿真学报，2021，33（9）：2166-2179.