联结·发现：小学数学结构化教学的节点

【摘 要】小学数学结构化教学需要准确把握数学知识结构、教材结构与学生知识结构，立足联结进行整体化教学，引导学生体验、感悟、发现知识间的联结，帮助学生形成结构化认知。还需要深入解读知识所蕴涵的思想方法、教材中的学习方法和儿童思维状态，立足联结发展学生的结构化思维。

【关键词】结构化 联结 融通

心理学研究表明，个体解决问题能力的高低不仅取决于个人所获得的有关知识的多少，还取决于知识的性质和组织结构，当头脑中的知识以一种网络结构的方式进行储存时，可以大大提高知识应用时的检索效率。

一、立足联结，优化教学分析

布鲁纳中说过：不论我们选教什么学科，务必使儿童理解该学科的基本结构。数学学科知识具有完整的网状结构，教材将这个系统的、网状结构的知识体系拆分成独立的知识点，通过螺旋上升式的编排呈现给学生。为了促进学生理解、感悟数学知识的基本结构，优化学生的认识结构，数学教学要有整体性视角，立足联结展开教与学。

（一）理清知识结构，发现联结

联结是形成知识结构的关键要素，在理解数学知识结构的基础上，理清教材中知识间的纵向、横向关联，有助于提升学生联结·发现的能力。

1.理清知识的纵向关联

理清知识的纵向结构是引导学生形成良好知识结构的基础。将关联的知识点按知识发展顺序串成一个知识链，通过兼顾单元整体解读与全学段内容解读，分析理解其教学顺序与作用、重点和策略，便可在教学实践中做好铺垫、沟通。在教学“分数的基本性质”时，本册分数知识的单元整体关联分析如表1。

由表1可知，分数的意义是种子课，是发现、直观理解分数基本性质的前提；分数与除法的关系是理解分数基本性质的逻辑基础，为类比推理意识的培养提供抓手；真、假分数为探索分数基本性质中更科学的不完全归纳验证提供了前提；分数相关的互化为学生自主验证提供了更多路径；通分与约分、异分母分数加减法是分数基本性质的应用。

2. 理清知识的横向关联

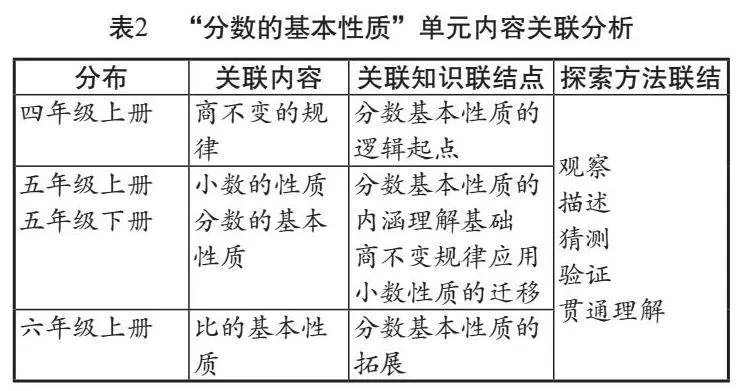
横向联系是通过类知识的关联分析，通透地理解这些数学知识是如何关联的，有助于理解这些知识点在教学时的路径和策略，理清知识的横向联系有助于学生将知识融会贯通、感悟数学思想方法、学习方法。“分数的基本性质”单元内容关联分析见表2。

在教学“分数的基本性质”时，教师不仅要引导学生通过操作验证分数的基本性质，还要通过商不变的规律来验证（简单推理），同时解释小数的性质，帮助学生将三个规律进行贯通，发展其迁移能力，为学生探索比的基本性质做好准备。

（二）分析学生现状，创生联结

结构化的教学不仅要关注知识间的关联，更要关注学生现状的分析，实现数学知识、学生现实经验与思维结构的融通。

“分数的基本性质”关联知识的学前调研数据如下：

（1）商不变规律表达：正确规范的约占78.3%，正确但是不完整的约占17.4%，不会的约占4.3%。

（2）学生举出与1/4相等的分数，主动找出多个正确例子的约占73.9%，举出一个例子的约占21.8%，不能举出的约占4.3%；要求学生独立验证时，约有91.1%的学生能顺利完成，第一选择利用化成小数进行验证的约占76.6%，利用画图验证的约占8.3%，利用“商不变规律”进行推理验证的约占6.2%。

（3）学生对小数性质的内涵理解，第一选择从单位解释的占78.2%，从计算单位理解（大小不变，计数单位改变）的占17.4%，其他的占4.4%。

（4）对探索运算律的回忆，有89.1%的学生能够说出通过举例验证。

以上数据分析显示：五年级学生对于商不变的规律掌握得较好，有利于用类比方法表述与解释分数的基本性质，利用联结能引导学生自主发现、表达分数基本性质。但是大多数学生没有用商不变规律来解释分数基本性质的意识，没有从分数单位理解分数基本性质的视角，需要教师适当引导。

二、立足联结·发现，重构课堂教学

“发现学习”理论强调注重利用知识联结、经验联结、方法联结与思想联结，激发学生主动探索，实现知识的再发现，通过联结实现认知结构的融通，进而优化学生的认知结构。在“分数基本性质”的教学中，笔者立足联结·发现设计了“释放想象，广泛联结—主动探索，协同发现—反思梳理，融合贯通”学习流程，让学生真正站在课堂中央。

（一）释放想象，广泛联结

师：（出示课题：分数的基本性质）看到这个课题，你能想到什么？

生：什么是分数的基本性质？

生：分数的基本性质是怎样发现的？

……

师：这些问题都非常有价值，并且有学生已经就“分数的基本性质和我们学过的哪些知识有关”进行了思考，有理有据，非常了不起。

师：有两位同学联想到商不变的规律与小数的性质，想想我们是怎样学习的？

生：是从一些例子中发现的，然后进行小结。

师：今天我们也从一些例子中去观察、比较，开始我们的探索之旅。

[评析]联结是形成结构化的节点，也是学生探索、想象的支点。利用课题引导学生展开联想，可以让学生对知识进行充分联结，为学生形成结构化认知和主动探索打下基础。

（二）主动探索，协同发现

师：（出示分数图，图略）圆中的阴影部分用哪些分数表示？仔细观察这些分数，你有什么发现，在小组里讨论。

生：我们组发现，有的分数阴影部分大小是相同的，有的部分大小是不同的。

生：我们组还发现，几个阴影部分相同的分数分子乘多少，分母就要乘多少。

师：能让大家听得更明白些吗？

生：分子乘2，分母也乘2，就得到；分子乘3，分母也乘3，就得到，这三个分数相同。

师：（动画演示）通过重叠，我们验证了你的发现是正确的，=，=。也就是一个分数把分子、分母同时乘上相同的数，是与它相等的新分数。是不是所有分数都有这样的现象呢？目前只是一个猜想，需要我们去验证，你们打算怎样验证？

生：我们可以多举一些例子，看看是不是都是这样？

师：下面在小组里先交流你们怎样去验证，再试一试。

生：我们把的分子、分母同时乘2、4、8，得到许多新的分数，它们和相等。

师：你们是怎样去验证它们相等呢，想到几种方法？

生：通过折一折我们就能发现=，=。

生：我们组还想到化成小数，它们都是0.5，所以是相等的。

生：不一定要计算出答案，可以把分数转化成除法，根据商不变规律可以知道，1÷2=2÷4，1÷2=4÷8，然后转化成分数就可以验证它们是相等的。

师：同学理一下，我们刚刚想了几种方法来验证？

生：化成小数、折一折、商不变规律。

师：有的同学们用商不变规律验证了这些分数与相同，你还能找到哪些与相同的分数？

生：、、，很多，说不完。

师：还有其他的例子吗？

……

师：验证这些分数相同，你喜欢哪种方法？

生：用折的方法不太方便，化成小数也是比较麻烦的，把它转化成除法算式，利用“商不变规律”来验证比较方便，而且感觉可以验证所有相同分数间的关系。比如，一个分数，可以写成b÷a，b÷a=（bc）÷（ac），把（bc）÷（ac）写出分数，就可以得到=。

师：看来分数的基本性质与商不变规律有很密切的联系，利用分数与除法的关系可以建立起这种联系，根据商不变的规律，你能联想到什么？

生：我想到分数的基本性质应该是：分数的分子和分母同时乘或除以相同的数（0除外），分数不变。

师：这里是分数的大小不变。为什么要补充“0除外”？

生：0乘0等于0，如果有了0，就不一定相等了。

师：也是没有意义的。

师：这就是分数的基本性质，与商不变的规律进行比较，你有什么想说的？

生：两个知识点很相似，连表述都一致，我想我们只要会其中一个，就可以推出另外一个。

生：分数的基本性质是分数中的规律，商不变规律是除法中的规律，就像分数与除法的关系，也有细微的差别。

[评析]通过小组交流、寻找与1/2相等的分数，引导学生归纳推理。同时抓住部分学生利用“商不变的规律”对分数基本性质进行解释说理的契机，引导学生进行类比表达。立足联结引导学生体会知识间的关联、结构、位置甚至知识间的不同，是优化学生知识结构的重要路径，也是增强学生应用类比迁移的方式进行学习能力的重要路径。

（三）反思梳理，融合贯通

师：（出示三年级下册例题）在学习三年级下册学习“认识一个整体的几分之一”时，例题描述“有6个桃，平均分给两只小猴”，当时有许多同学很困惑为什么要用表示，不能用表示，学习了分数的基本性质，你觉得当时你的困惑有道理吗？

生：它们的大小其实是一样的，只是意义不一样。

师：（出示数轴）这个点可以表示哪些数？

生：。

生：也可以表示、，因为图上只有一个点，并没有平均分成10份，也可以平均分成100份、1000份。

生：那也可以表示为0.3 。

生：还可以表示为0.30、0.300，可以表示所有与0.3相等的小数。

师：那这些数有什么联系与区别呢？

生：他们的大小相同，计数单位不同。

生：他们表示的意义不同，书写也不同。

生：0.3=，0.30=，0.300=，利用小数的意义，分数的基本性质可以用来解释小数的性质，他们的规律是相通的。

师：看来同学们的认识角度很多，比较深刻。请在数轴上画出一个点来表示。

师：有的同学很快就完成了，你们有什么技巧吗？

生：因为=，所以这两个分数可以用同一个点表示，我们只要找到表示的点，就可以表示。

师：感受到分数的基本性质有什么作用吗？

生：应用分数的基本性质可以将一个简单的分数变成一个复杂的分数，或者将一个复杂的分数简化成一个简单的分数。

师：（课件呈现旧知）回顾我们是怎样探索分数基本性质的，你有什么收获？

生：我们先观察一些分数，发现有的分数分子、分母不同，分数大小却相同；根据发现猜想是不是许多分数都有相同的现象，然后通过举例子来探索；通过折纸、化成小数、化成除法算式可以验证这个发现。

生：我知道了分数的基本性质，将一个分数的分母、分子同时乘或除以一个相同的数（0除外），分数的大小不变。

生：和小数性质一样，根据分数基本性质可以在分数大小不变的基础上改变分数的计算单位。

生：我知道很多知识是有联系的，小数、分数与除法有着相似的规律。

生：可以从多种角度来认识分数与分数的基本性质。

[评析]我们在“解决问题的策略”“综合与实践”的学习中，都有回顾与反思环节，本课属于探索、发现规律的课型，引导学生进行回顾反思，不仅能让学生发现知识本质内涵、思想方法上的联结，还能让学生通过不同视角理解知识本质，实现知识、方法上的融会贯通。

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022

[2]席爱勇，何杰. 结构关联：小学数学结构化学习的学理探究[D].淮安：淮阴师范学院学报（自然科学版），2018（12）