划阶·定阶·进阶：基于SOLO分类理论的学习进阶策略研究

【摘 要】本研究基于SOLO分类理论，以“四边形的认识”为例，探讨学习进阶策略：通过学理分析明确学习进阶的终点、维度和水平，实现“划阶”；通过学情调研确定学习进阶的锚点，实现“定阶”；通过设计进阶教学策略，实现“进阶”。此研究为小学数学学习提供新的教学视角，为小学数学教学研究提供参考。

【关键词】SOLO分类理论 四边形的认识 学习进阶

设计符合学生认知发展规律的学习路径，促进学生高阶思维的形成，一直是教育领域关注的焦点。SOLO分类理论作为一种揭示学生学习思维层次的质性评价理论，和学习进阶理论一起，共同为小学数学学习研究提供了新的视角。本研究以SOLO分类理论作为分析工具，以“四边形的认识”为例，通过学理分析厘清进阶层次、学情评价确定进阶锚点、学路设计探寻进阶策略，探索学习进阶策略。

一、划阶：基于SOLO分类理论的进阶层次厘清

一个概念、一个课例并非孤立存在，学理分析围绕知识本源、课标素养、教材编排等维度，自上而下对学习内容进行结构化解读，聚焦课例概念并兼具整体视角。在基于SOLO分类理论的概念学习进阶中，通过学理分析明确进阶终点、区分进阶变量、预设进阶层次水平，定目标、定维度、定表现，解决“去哪里”的问题。

（一）确定进阶终点：定目标

进阶终点即课堂学习目标，是学生在一个主题学习结束时所能达到的最高水平。进阶终点的确定主要通过以下方面：首先，对数学本源、内容领域、素养指向等整体分析，宏观把握学习远点；其次，通过课标解读、教材分析初定进阶终点；最后，对初定目标进行质性描述并形成进阶终点。

以“四边形的认识”为例，通过知识本源解读，可知四边形的概念通过“发生式定义”方式定义，而在小学教材中均没有给出明确的定义，只是通过整体感知和认识特征等方式认识四边形。如内容领域方面，该内容属于图形与几何领域中图形的认识板块。小学数学图形的认识编排体系遵循“体、面、线、面、体”的逻辑顺序，经历“实物、图像、表象、抽象”逐步数学化的概念形成轨迹，体现螺旋式上升的特点。有关四边形的内容一共出现了三次，本课内容为第二次，首次从边和角数量两个维度定性地认识、描述图形，也就是要求达到描述、分析的几何思维水平。另外，该内容的主要核心素养是空间观念，发展空间观念的常用策略为观察、操作、想象等，是不可或缺的，而在操作、语言和想象等直观层面逐步抽象并形成丰富的表象则显得尤为重要。由此，本内容的进阶终点可初定，并基于SOLO分类理论进行修正，目标层级质性描述确定为“能严密地描述四边形内涵并明确四边形的外延，能清晰表达四边形相关图形之间关系”。

（二）区分进阶变量：定维度

进阶变量也称之为进阶维度，是追踪描述进阶水平的关键要素，其选取是学习进阶研究的核心工作。基于SOLO分类理论进阶变量可通过知识本源、课标素养、教材编排等学理整体分析确定。再者，作为基础几何图形概念课，一般可从图形定义、图形特征、图形关系等方面确定进阶变量。如“四边形的认识”，本课之前只要求学生从整体直观水平认识四边形，本课首次要求从边和角数量两个维度定性地认识、描述图形。那么，“辨析四边形”“四边形的描述维度”“四边形相关图形间的关系”可作为进阶变量。

（三）预设进阶水平：定表现

学习进阶水平是具有一定理解力的学生在完成某一类型的学习任务时应具备的具体表现，不同的进阶水平及表现可根据进阶终点结合进阶变量进行确定。如“四边形得认识”的进阶水平表现描述如图1。

水平划分 层次 进阶变量 水平表现

水平0 前结构 1.辨析四边形；

2.四边形的描述维度；

3.四边形相关图形间的关系 无法描述（辨析）或者描述混乱

水平1 单点结构 能直观辨认或者能用一个特征来描述（或辨析）四边形，能正确辨析部分四边形但会出现错误选项

水平2 多点结构 能用两个及以上特征来描述四边形，能正确辨析部分四边形但会出现某类别漏选（只能正确辨析特殊四边形或一般四边形），未形成四边形的完整认知

水平3 关联结构 能较完整描述四边形的特征或正确辨析四边形，能对四边形与特殊的四边形关系有所感悟

水平4 抽象扩展结构 能严密地描述四边形内涵并明确四边形的外延，能清晰表达四边形相关图形之间关系

二、定阶：基于SOLO分类理论的进阶锚点精准

学情评价主要通过试题设计、访谈调查和数据分析等步骤进行。学情评价对于把握学生认知经验起点，明晰学生思维水平，进而精准确定进阶锚点至关重要。

（一）试题设计问卷访谈

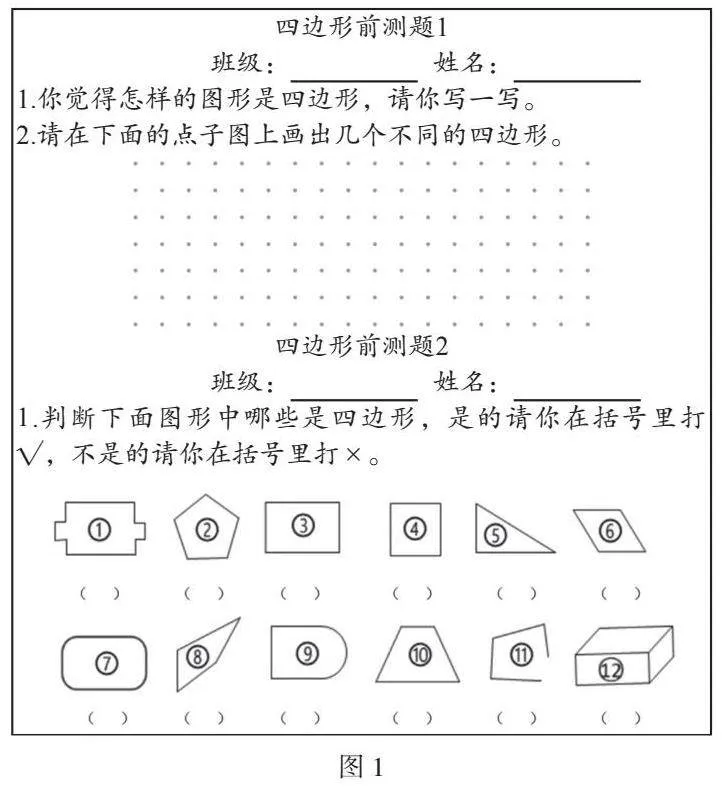
试题设计作为检测工具，是学习进阶的重要步骤，是追踪学生学习动态的主要工具。在基于SOLO分类理论的学习进阶试题设计中，一般设计开放式或半开放式的问题（或是相对封闭的层次性题组），常需通过多次设计及试测循环才能确定。如“四边形的认识”课前测试题历经三次设计及试测修改，最后课前测试题设计如图2。三道测试题主要检测学生对四边形的辨析及描述水平，题1-1主要测试学生对四边形的描述水平，题1-2测试学生四边形表象的建构水平，题2-1测试思维冲突下四边形的辨析水平。

问卷访谈一般以班级为单位选取一个或多个进行全样本调研，调研方式一般为书面问卷（或网络问卷）结合个别访谈。如“四边形的认识”选取某校三年级某班40个学生作为被试对外进行全员问卷及个别访谈。

（二）数据分析精准锚点

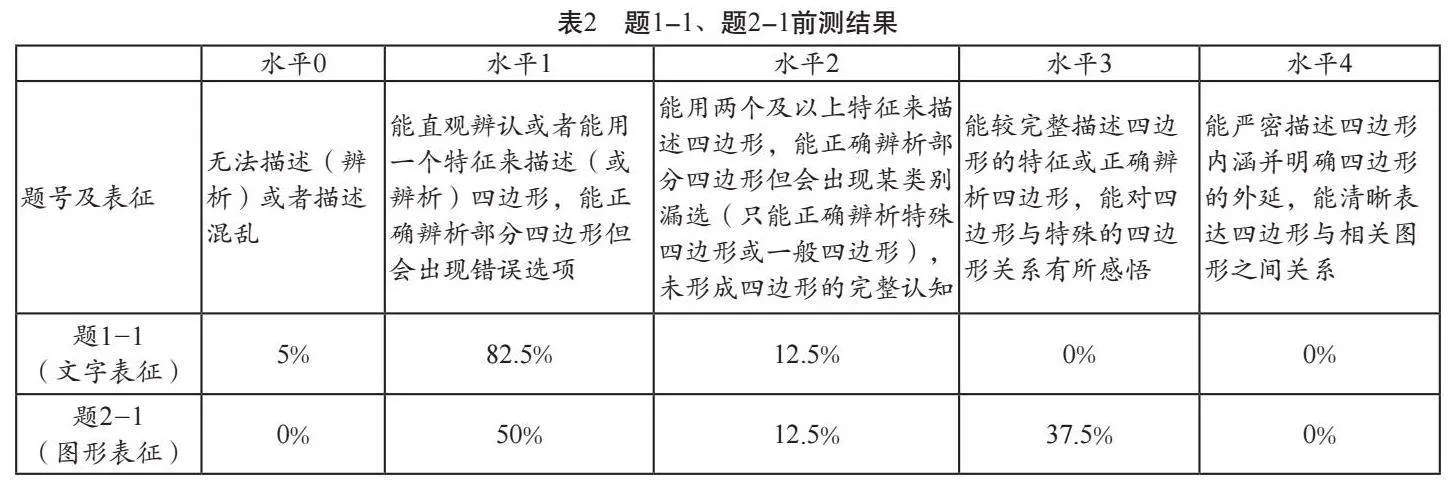
数据分析一般根据进阶水平表现进行分类汇总，并结合进阶变量进行深入分析，最终明晰认知经验起点及思维水平层次，精准确定进阶锚点。以“四边形的认识”为例，测试人数40人，前测结果数据汇总如图3、图4、图5。

由此，可以精准确定以下进阶锚点：

1.大部分学生能在点子图中正确画出四边形，能在各类图形变式中正确找出四边形，学生存在二元对立现象，对概念外延的理解及表象建构比较“片面”，说明学生几何思维水平已经达到整体直观水平，具备较好的进阶基础。

2.结合SOLO分类理论分析，大部分学生能基于边、角等元素写出四边形的部分特点，但部分学生仅限于从单一元素描述特点。文字表征方面没有学生可达到“关联结构”水平，突破表征方面仅有37.5%的学生可达到“关联结构”水平，多数学生尚未达到SOLO分类理论“关联结构”水平，也未完全达到几何思维“描述/分析”水平。

三、进阶：基于SOLO分类理论的进阶策略探寻

（一）进阶策略

进阶策略可通过结构化学材、结构化问题、结构化环节来实现，以结构化的教促成有关联的学，促成学生思维进阶跃升，探寻收获进阶策略如下：单点感知、多点勾连、结构关联、拓展融通。

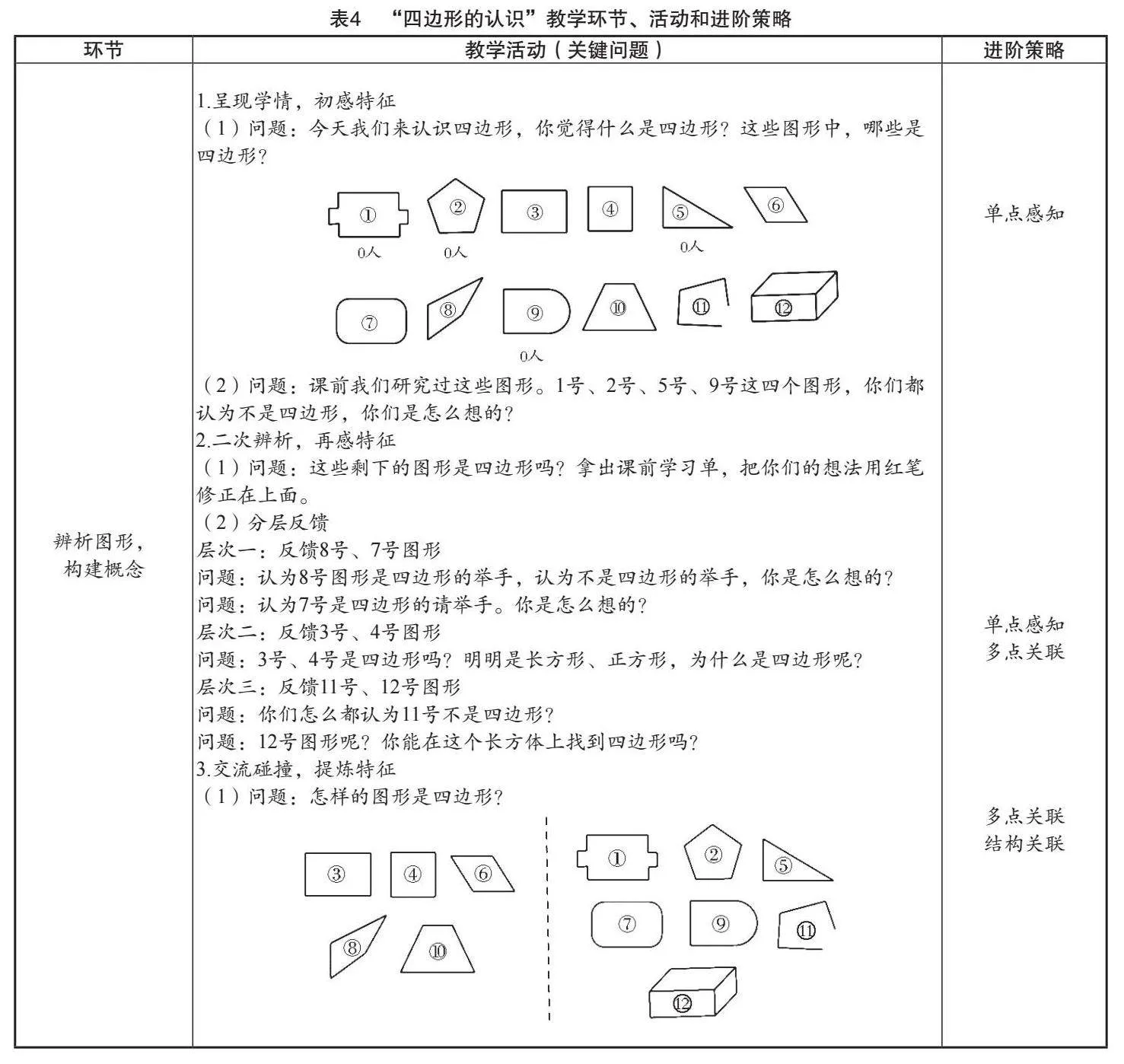
（二）课堂生成

课堂具体教学环节、活动、进阶策略等课堂生成见表1。

综上，本研究基于SOLO分类理论，以“四边形的认识”为例，通过学理分析、学情调研、学路设计，探索学习进阶策略，可为相关研究提供了有益借鉴。