计算思维驱动下的模块化问题解决活动探究

【摘 要】《义务教育信息科技课程标准（2022年版）》提出，要更加注重学生问题解决能力的培养与提升，倡导通过结构化的教与学，帮助学生重塑科学认知结构，提升思维品质。计算思维作为信息科技学科核心素养中的关键性素养，对学生认知方式的重构具有重要价值导向作用。基于问题解决模式下的计算思维实践，主要是通过结构化、模块化、系统化的问题解决过程，帮助学生重构认知结构，实现问题解决方案的最优化，充分体现了在解决问题过程中对问题解决过程的控制与管理，实现了精准化、高效地解决问题。

【关键词】计算思维；模块化；问题解决；核心素养

【中图分类号】G434 【文献标志码】A

【论文编号】1671-7384（2024）011-053-03

深刻理解新课标中计算思维的内涵

计算思维作为信息科技学科核心素养，已经成为学生解决问题能力提升与发展的关键性素养。其中，在《义务教育信息科技课程标准（2022年版）》中关于“过程与控制”模块教学，明确提出了“输入—计算—输出”的计算模式，成为计算思维在小学阶段的具体实践。具体来说就是通过将生活中具象的问题进行科学有效的抽象，并用计算机科学的视角界定问题，形成计算机可以解决的问题，即完成“输入”的过程，计算机通过“计算”的方式，求出问题最优的解决方案。这样的“计算”过程可以是“编程”的过程，即用编程的方式进行模拟验证，从而形成问题解决的具体模型。最后，采用数字化、形式化的表征方式，实现对问题的有效“输出”。

计算思维活动建构与支撑理论

基于“输入—计算—输出”的计算模式，作为问题解决模式下计算思维实践的过程性框架，能够帮助学生重塑认知结构。首先，通过向计算机发送指令，完成“输入”的过程。然后通过“计算”，形成问题解决的具体方案，并且对方案进行科学有效的验证，即通过编程的方式进行验证。最后，实现任务的有效解决，即将最佳的问题解决方案通过不断循环迭代，形成具有可操作性的问题解决模型后再“输出”。

1.活动主题的设计与方法的渗透

以小学生真实的生活背景来激发学习兴趣，笔者构建了“智能快递小车”项目案例。通过模块化的设计方式将该案例分解为三个主要部分，即小车使用灰度传感器实现循线自动驾驶、路口自动停车并自动规划路线、寻找出到达目的地最佳线路。为了高效率达成取货和送货的目的，学生在设计与制作小车的过程中必须考虑到小车的稳定性和提升小车速度等间接因素。笔者基于系统化的设计理念，将项目问题进行有效分解，形成多个相对比较容易解决的子问题。在此基础上，通过模块化的“组装”，将多个微型系统通过顺序、选择、循环等逻辑实现有效组合，形成具有一定智能化的快递小车。整个项目活动的设计，满足了基于问题解决模式、计算思维驱动下，对问题解决的过程与控制的素养要求。

2.学习案例的知识元与过程迭代

真实有效的项目案例，需要深度挖掘生活中的具体应用场景后，进行模块化设计。“智能快递小车”项目案例的设计，是以小学生对旅游景点参观线路规划的初步感知和乘坐电梯的真实体验为基础，通过对具体问题的有效抽象，进行结构化的设计与建构。抓住小学生生活中的元素，激发学生的学习兴趣，针对问题本质的探究，使学生能够有真实的体验，从而避免了空洞的问题探究。生活中线路的规划、电梯运行等都是基于“输入—计算—输出”的基本过程，通过“人机交互”的方式，实现系统化的模型应用，在输入与输出的过程中，构建了模块化的问题解决流程与结构，重点体现了人在解决问题时对过程的控制。

素养导向下“教—学—评”一致性活动设计

笔者通过基于问题解决模式下的计算思维实践过程，进行了结构化的项目活动设计。从生活中关于“输入—执行—输出”这种运作方式出发，将生活中具象的过程与控制进行抽象，形成了“输入—计算—输出”的问题解决模式。为了实现“教—学—评”一致性，笔者以项目式学习的方式让学生主动且真实有效地参与到学习活动中。同时，将终结性评价转变为形成性、过程性评价。笔者认为“教—学—评”一致性的课堂教学模式，本质上是一种结构化的课堂模式，能够有效提升课堂教学的效率，真正实现以学定教、以教促学、以评定教的高效课堂。

1.学生初步感知智能交互过程

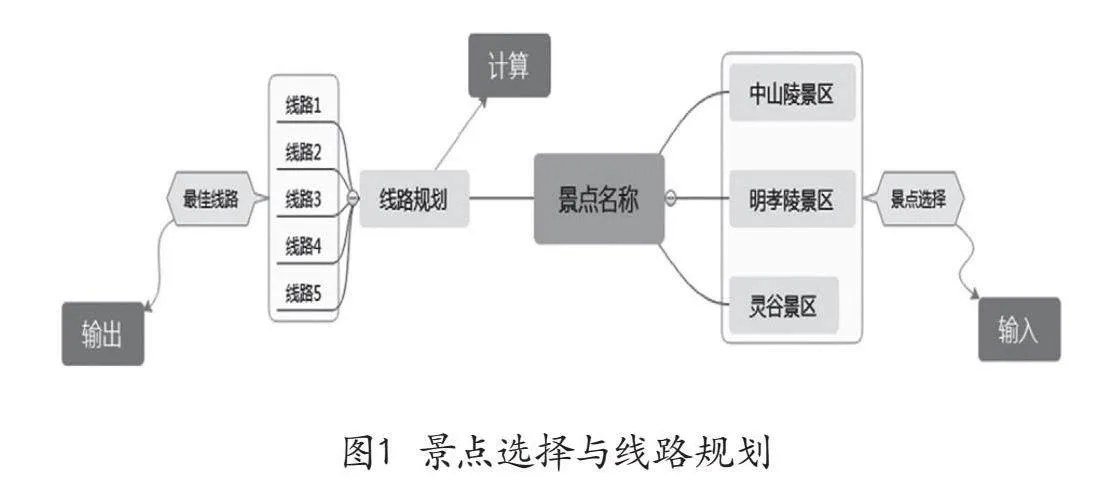
笔者给学生讲述导航的过程。在过去没有导航系统的时候，人们到陌生的地方都是需要带着地图的，不然很难找到目的地，还容易迷路。人们通常在地图上找到出发地和目的地的位置，并找出几条到达的线路，最后比较几条线路，找出最佳的线路。随着人工智能的应用，人们已经不再需要烦琐的人工操作，只需要输入指令，人工智能通过计算与科学规划，给出最佳的线路方案。例如，当人们想要参观“中山风景区”，通过景点出入口的人工智能机器人，选择想要参观的景点，智能机器人就会规划出最佳的游览线路。

核心素养下的设计意图：从景点选择到线路规划，以及提供最佳线路的过程，如图1所示，该过程本质上是由人与人工智能机器的交互过程，即通过输入指令，人工智能机器根据所输入的指令进行计算，输出最优的计算结果。学生通过这样的过程初步感知智能交互的基本逻辑，即“输入—计算—输出”的执行模式。

2.学生深度体验过程与控制

笔者请学生讲述乘电梯的过程：生活中乘坐直升式电梯，输入相应楼层号码呼叫电梯，等待电梯停靠到我们所在的楼层，在这个过程中电梯会根据电梯所处的楼层位置，计算电梯需要达到的楼层和所要执行的过程，最后电梯到达我们当前所在的楼层后自动打开电梯门；当我们进入电梯后，需要输入想要到达的楼层号码，电梯会进行计算，如果是上行，则会计算我们所在楼层以上是否有人呼叫上行指令，如果有，电梯则会停靠到相应楼层。

核心素养下的设计意图：乘坐电梯真实的体验，帮助学生深度感受其中的过程与控制。无论是呼叫电梯的过程，还是电梯升降停靠的过程，该过程可以看作是一个微型的系统处理过程，即由“输入—计算—输出”三个部分组成。

3.学生模块化解决真实问题

学生体验电梯运行的过程，初步建立了电梯运行的概念模型，即“输入（呼叫）—计算（执行）—输出（停靠）”。从模块化视角进行结构化处理，能够形成可计算的数学模型。其中，电梯运行过程结构模块主要有控制电梯上下运行、控制电梯停靠的楼层、电梯楼层的呼叫与判断。基于该结构模型，笔者设计了“智能快递小车”项目，通过模块化分解问题，将智能快递小车项目分解为三个主要模块，即小车循线行驶、小车路口停车和小车线路规划。

（1）智能快递小车之循线行驶

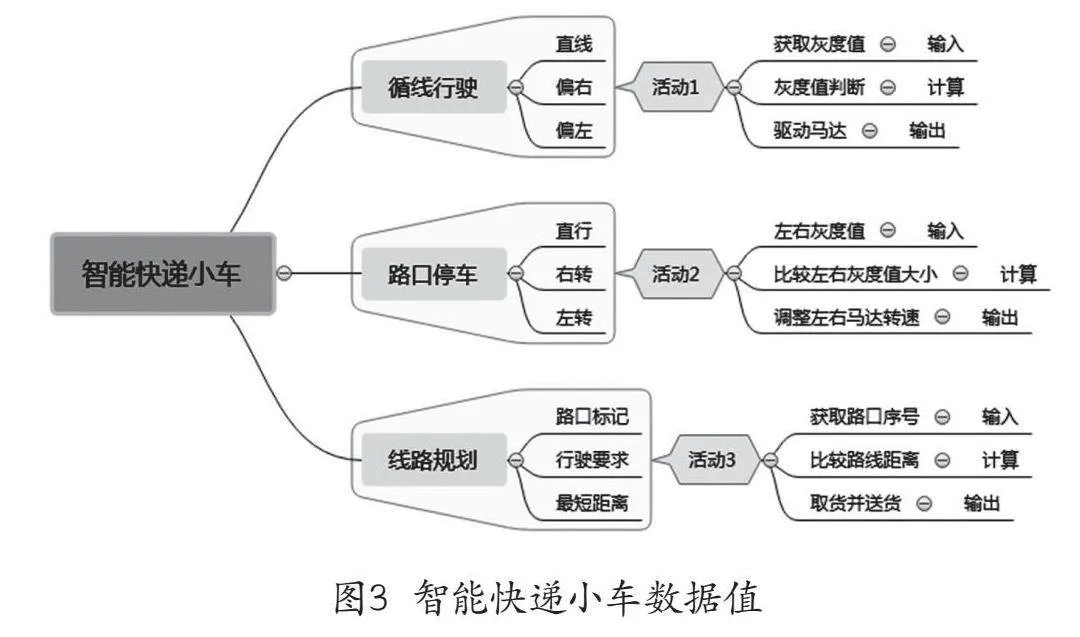
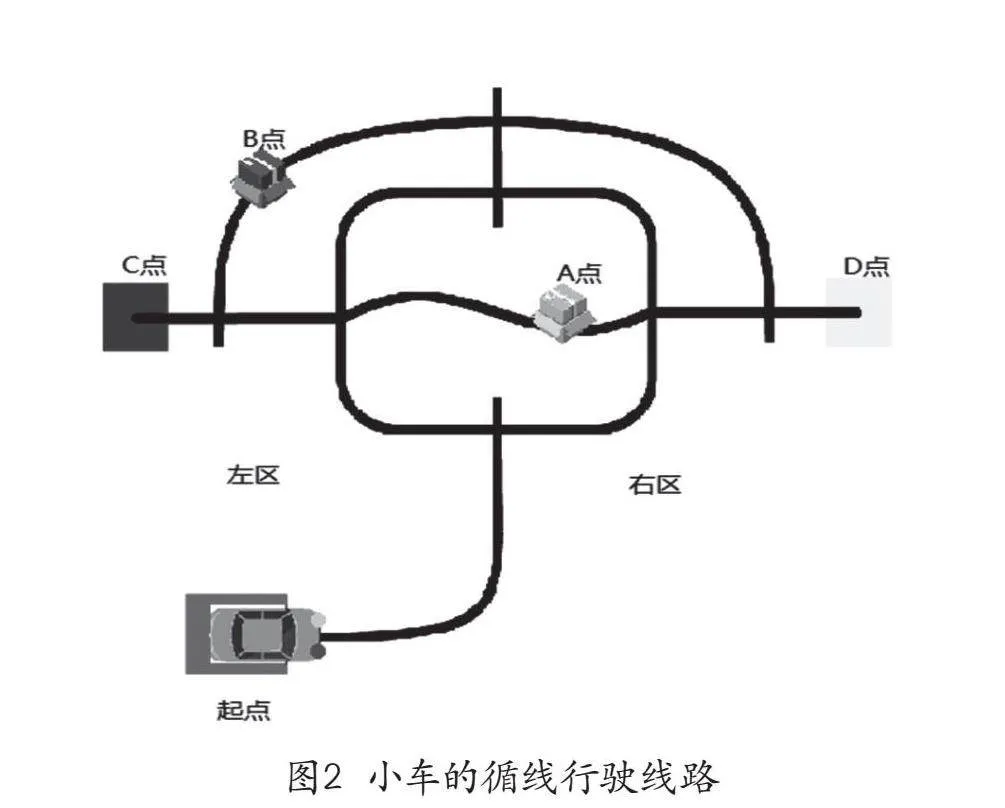
智能快递小车通过获取线路的灰度值，根据灰度值判断行驶线路，驱动马达实现小车循线行驶。灰度传感器是一种光电传感器，通过发射光线并接收反射回来的光线来判断地面的颜色，当传感器检测到黑色线条时，它会返回一个较低的灰度值，因为黑色表面吸收了更多的光线，而当传感器检测到非线条区域（通常是白色或浅色的地面）时，它会返回一个较高的灰度值。小车根据获取到的灰度值判断行驶线路，驱动马达实现小车循线行驶。如图2所示，学生通过对小车的循线行驶进行问题抽象，形成了由灰度值控制马达转动的概念模型，通过判断小车的左右灰度值的大小，建立控制小车正常循线行驶的结构模型，实现小车循线行驶的微型系统。

核心素养下的设计意图：通过让学生实现小车的直线行驶、小车偏右、小车偏左状态的纠偏，实现小车循线行驶，让学生理解并掌握小车行驶的基本原理，通过过程与控制的方式，实现微型功能系统的建构，即实现小车的循线行驶。

（2）智能快递小车之路口停车

车辆在行驶过程中需要进行相应的判断，这个过程主要是通过“计算”实现的，即在路口停车，通过计算判断当前路口灰度值的状态，输出相应的指令，小车是直行、右转还是左转等操作，该过程是条件判断语句结构。如图3所示，学生在活动的过程中通过获取灰度值、比较灰度值、调整马达转速等操作，可以看作是实现智能快递小车在路口停车的微型系统。

核心素养下的设计意图：让学生从生活中的直接经验获得对小车状态检测过程的理解，帮助学生迁移到智能快递小车在路口停车的计算判断过程。小车通过获取到的左右灰度值，比较左右灰度值大小，根据计算结果调整小车的左右马达转速，从而实现小车在路口停车，进行直行、右转、左转等操作。

（3）智能快递小车之线路规划

智能快递小车要实现取货和送货的目的，就必须根据相应的规则进行货物的转运，需要具有线路规划的功能。智能快递小车将相应的货物运转到目的地，根据图2的线路示意图进行具体线路规划，实现货物的高效转运。该货物转运过程可以看作是一个微型系统。

核心素养下的设计意图：通过引导学生根据线路示意图进行具体线路的规划设计，让学生体验“计算”的过程。同时，通过结构化的分析、模块化的处理，实现微型系统的有效组合，建构完整的智能快递小车。

4.项目任务分析与评价

针对“智能快递小车”项目设计，宏观上采用了基于“输入—计算—输出”计算模式，而在处理具体问题时则通过基于问题解决模式下计算思维实践过程，即抽象层、建模层、表征层等。通过模块化的任务分解，形成小车循线行驶、小车路口停车、小车线路规划等任务模块。此外，每个具体任务就是一个微型系统，通过模块化的“组装”，完成一个综合项目。

采用模块化的问题解决方式，实现对问题的过程与控制，提升项目开发的速度和质量。而针对项目案例活动的评价，则以形成性评价、过程性评价相结合的方式，激励学生从被动式的学习转变为积极主动的探究学习。例如，智能快递小车在行驶的过程中，学生如果能够对位置的偏转进行深入探究，会发现小车的偏转会有完全偏转和部分偏转两种状态，进而学生可能会总结出影响小车行驶稳定性的因素等。针对项目的迭代与优化方面进行评价，可以在现有项目的基础上，形成一般性的问题解决方法，即“输入—计算—输出”的计算模式。同时，还可以从学生对问题的抽象、建模、表征等过程， 对学生计算思维发展进行评价。

结束语

以问题解决为基础的计算思维实践过程，能够重塑学生认知方式，提升学生解决问题的能力。采用模块化的问题解决方式，可以提升问题解决的效率，让学生更好地理解并掌握系统模型的建构过程与方法。在模块化的问题解决过程中，能够有效促进学生认知模型的建构，在不断迭代的过程中抓牢解决问题的过程与控制。