“怎样解题表”用于添加辅助线的教学实践

摘 要：在初中数学学习中，经常出现学生对数学知识理解不深刻的现象，严重影响数学教学质量的提高.基于此，笔者依据波利亚“怎样解题表”，设计了两道难度递进的几何证明题的教学过程.在教师的引导下，学生展开有效思考，适时进行多次回顾总结，在经历“坍塌又重建”的过程后，扎实积累“根据图形结构特征，适当添加辅助线”的解题经验，帮助学生加深对所学知识的理解.

关键词：怎样解题表；初中数学；几何证明题；辅助线

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）29-0023-03

收稿日期：2024-07-15

作者简介：江瑜琪（1999.5—），男，浙江省宁波人，湖州师范学院研究生（在读），从事中学数学教学研究.

波利亚认为，教师要教给学生的不单单是知识本身，最重要的是要教会学生思考及怎样思考［1］.在日常教学实践中，笔者发现学生学习停留于知识表面.究其原因，是其明所为，亦不明何为.数学教学的关键在于引导学生展开有效思考［2］.“怎样解题表”是《怎样解题》的核心内容，将解题过程分为“理解问题、拟订计划、执行计划、检验回顾”四个步骤［3］.笔者计划在一堂专题课上，依据“怎样解题表”完成两道由易到难的几何证明题的教学，通过适时回顾总结，促进学生展开有效思考，深刻理解知识间的联系，帮助学生积累解题经验.

1 建于基础，隐于深处

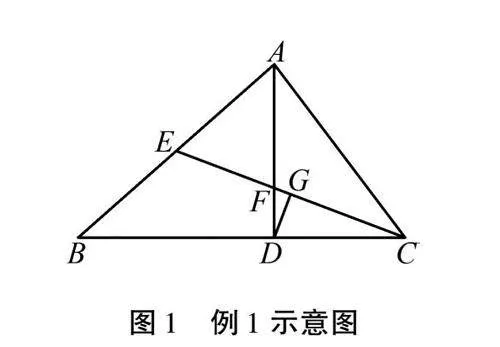
例1 如图1，在△ABC中，AD是BC边上的高，CE是AB边上的中线，G是CE的中点，连接DG，CD=AE，CE与AD交于点F.求证：DG⊥CE.

1.1 理解题目

在教学过程中，教师需预留一定时间让学生读题思考，寻找题目的未知量.此题需证明DG⊥CE，可将已知条件进行分类，其中“AD是BC边上LcTcUa+nO5uuaEmKazekaw==的高”“CE是AB边上的中线”“G是CE的中点”这三个条件可以归为一类，都与“三线合一”有关，“CD=AE”可以归为一类.

1.2 拟订方案

阅读题目后，学生已能够对一部分简单条件进行转化.例如，“AD是BC边上的高”意味着“△ABD与△ADC是直角三角形”；“CE是AB边上的中线”意味着“点E是边AB的中点”；“G是CE的中点”意味着“DG是边CE上的中线”.对于条件“CD=AE”，学生短时间内无法将其合理转化应用，教师应在此处展开相应的引导.在讲解过程中，师生都应明确需“将所有的条件进行串联”，那么如何串联成为教学重点，教师可以设计问题串：“CD=AE”对于结果的证明有何帮助？如何将该条件与其余条件进行联系？具体怎么操作呢？

本题需要证明线与线之间的垂直关系，对于八年级的学生而言，关于直线垂直关系证明的知识储备较为有限，教师可以引导学生从“三线合一”入手，据此找出对应的等腰三角形.

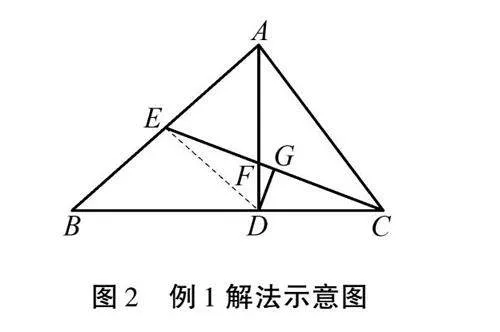
根据图形特征，图1中并没有等腰三角形，教师在此处可提出问题：根据哪些条件能够构造等腰三角形？如何运用已知条件构造等腰三角形？由此，学生再一次阅读题目，并进行深入思考.部分学生会发现，已知条件中还有一条高线，并且能够意识到需要“添加辅助线”解决问题，如图2所示.

1.3 执行方案

方案拟订后，教师还需带领学生验证方案的可行性.对于本方案，在拟定过程后，思路已经明确，因此在讲解中，教师可以适当加快速度，并进行板书.连接DE后，由“AD是BC边上的高，CE是AB边上的中线”可得△ABD是直角三角形，且AE=EB=ED.结合已知的“CD=AE”，通过等量代换，可以得到DE与CD之间的相等关系，由此判断△DEC为等腰三角形，联系“三线合一”，也就能够得到DG⊥CE，从而完成本题的证明.

1.4 回顾全程

在解答证明题时，若正向思考行不通，则需及时考虑逆向推导.解答此题前，学生在七年级学习了与平行线相关的辅助线添加方式.近期在学习三角形的相关内容中，接触了作高线、角平分线、中线等辅助线的方法，但总体上对“辅助线”的添加不熟练.推导过程中，若学生能意识到已知条件之所以无法串联，是“桥梁”缺失造成的，便可探究如何有依据地创建“桥梁”，凭空捏造的臆想难以支撑，“公理、定义、基本事实”等方为砥柱.

2 立于新颖，匿于创生

当学生面对更为复杂的问题时，例1的解题流程是否适用？需学生具备哪些能力？教师又应如何基于“怎样解题表”引导学生积累添加辅助线的经验？为此，笔者展示另一道几何证明题进行阐述.

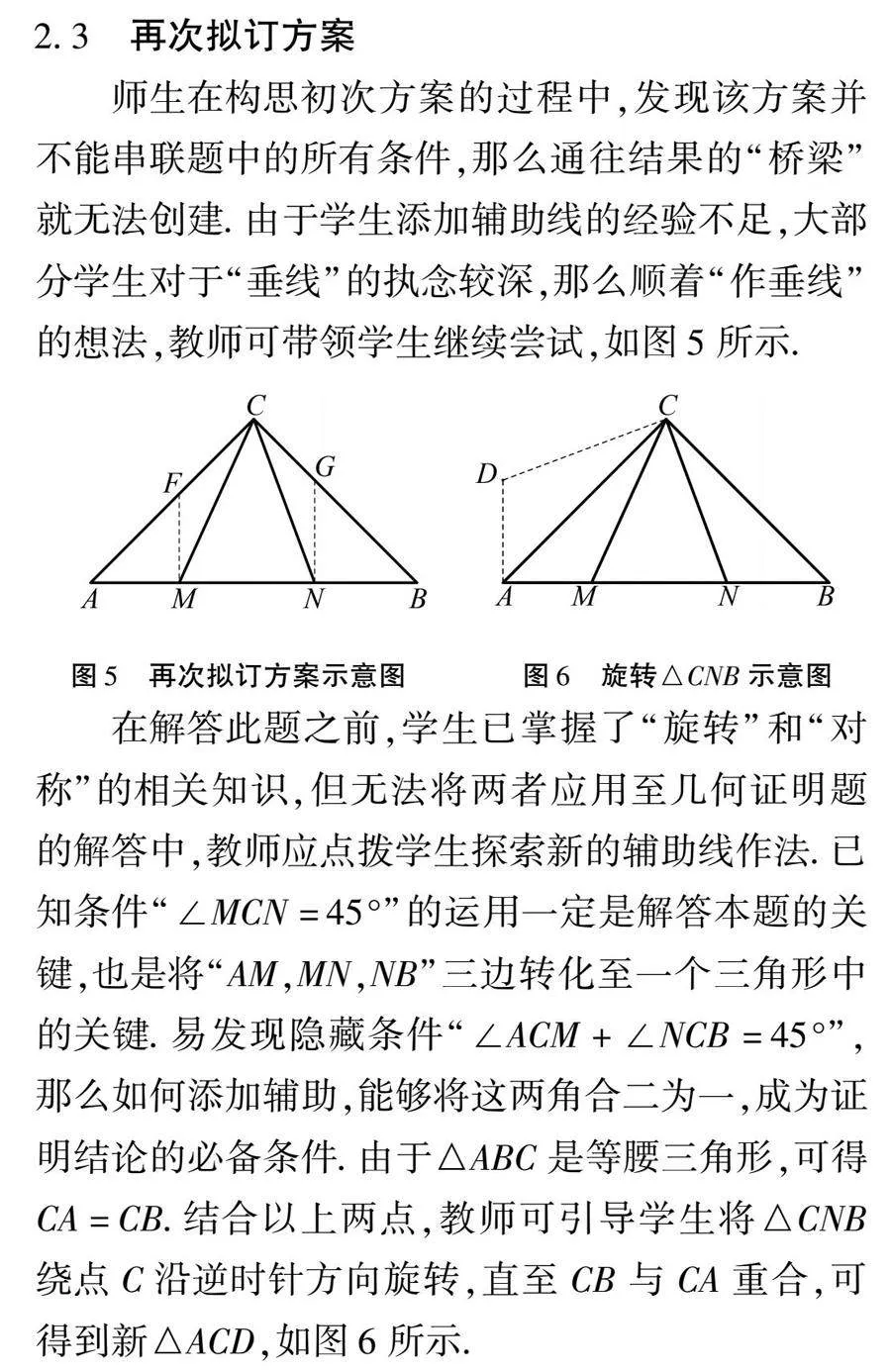
例2 若点M，N把线段AB分割成AM，MN和BN三部分，且以AM，MN和BN为边的三角形是直角三角形，则称M，N是线段AB的“勾股分割点”.如图3，在△ABC中，∠BCA=90°，AC=BC，点M，N在斜边AB上，且∠MCN=45°.求证：M，N是线段AB的“勾股分割点”.

2.1 理解题目

通过阅读，学生可将已知条件“∠BCA=90°”与“AC=BC”归为一类，由此可得出△ABC为等腰直角三角形；再将“∠MCN=45°”归为一类.

2.2 初次拟订方案

从结果出发，要证明M，N是线段AB的“勾股分割点”，此处有两个思路可供参考：一是将三条线段转化至同一个三角形中，通过证明由这三条线段组成的三角形是直角三角形，得出M，N是“勾股分割点”；二是通过代数的方法得出AM2，MN2，NB2三者的关系，若能得出两者之和等于第三者，即证M，N为“勾股分割点”.阅读完题目中的剩余条件，发现没有任何数据信息，否定第二条思路，教师应引导学生探索第一条思路.

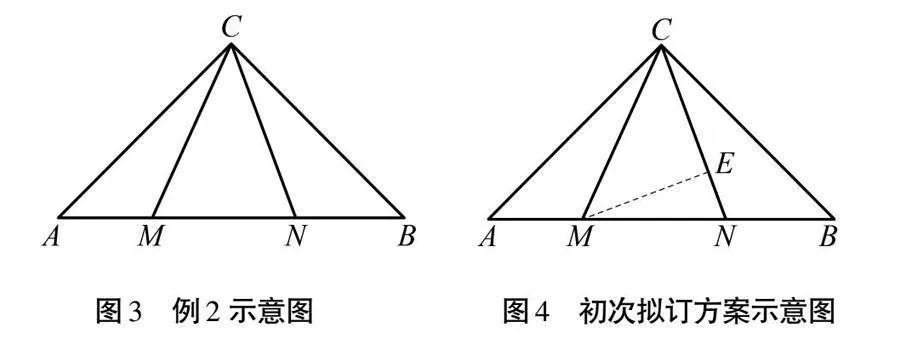
假定学生根据结论思考，结合新定义，会认为高线的添加更具有合理性.教师通过这条线索，假设学生提出“过点M作线段CN的高线，垂足为E”的想法，若没有学生提出，则教师自行陈述引导，作出该条辅助线，如图4所示，并向学生提问：“∠MCN=45°要怎么用进去呢？”有学生也许会抢答：“△MEC为等腰直角三角形.”这位学生的回答尝试将∠MCN进行应用，但很快被其他学生否定了.虽然△MEC为等腰直角三角形，但这一条件并不能将AM、MN、NB三边联系在一起，初次拟订方案失败.

2.3 再次拟订方案

师生在构思初次方案的过程中，发现该方案并不能串联题中的所有条件，那么通往结果的“桥梁”就无法创建.由于学生添加辅助线的经验不足，大部分学生对于“垂线”的执念较深，那么顺着“作垂线”的想法，教师可带领学生继续尝试，如图5所示.

在解答此题之前，学生已掌握了“旋转”和“对称”的相关知识，但无法将两者应用至几何证明题的解答中，教师应点拨学生探索新的辅助线作法.已知条件“∠MCN=45°”的运用一定是解答本题的关键，也是将“AM，MN，NB”三边转化至一个三角形中的关键.易发现隐藏条件“∠ACM+∠NCB=45°”，那么如何添加辅助，能够将这两角合二为一，成为证明结论的必备条件.由于△ABC是等腰三角形，可得CA=CB.结合以上两点，教师可引导学生将△CNB绕点C沿逆时针方向旋转，直至CB与CA重合，可得到新△ACD，如图6所示.

2.4 实施方案

在△ACD中，AD=NB，据此可建立NB与AM之间的关系，此条件也与之前的初步思路相吻合，目前只剩下MN并未与两边相结合.学生能够发现∠MCN=∠MCD，并且CD=CN，而CM为公共边，连接DM，易得△CDM≌△CMN，从而将MN化为DM，如图7所示.至此，三条线段都在△ADM中，而∠MAD=∠MAC+∠DAC=90°，易证结论成立.

2.5 探索新方案

学生运用旋转完成了例2的证明.教师继续提出问题：能否利用“对称”证明呢？∠ACM+∠NCB=45°，能否对∠MCN进行拆解呢？有了之前证明的铺垫，学生思路随之打开，既然能将△CNB进行旋转，同样也能以直线CN为对称轴，将△CNB进行对称变换，得到新△CNG，而NG=NB，实现了初步的转化.还有一边如何转化？教师将问题抛给学生，根据证明三角形全等的思路，连接MG，因为∠ACM+∠NCB=45°，那么∠ACM=∠GCM，前者通过角的相加得到全等，后者通过角的相减得到△AMC≌△CMG，从而AM=MG，且∠MGN=90°，易证结论成立.

2.6 回顾反思

完成证明后，教师应点明新的辅助线作法——旋转、对称，让学生明白辅助线不仅仅局限于作高线、角平分线、中线，突破学生的固有的知识框架.

结合例1，逆向推导的方式仍旧适用，但两题相对比，例2串联结论与已知条件的“桥梁”跨度更大，构造的难度随之递增.同样，例1的构造是建立在“直角三角形斜边上的中线等于斜边的一半”的基础上，例2则是依托于勾股定理，两题的底层逻辑一致，但后者的灵活性更强，需要学生有更为扎实的基础知识.学生在日后遇到类似问题时，须不断尝试探索，不断完善自身的知识结构，从而积累“根据图形结构特征，适当添加辅助线”的解题经验.

3 结束语

在问题解决过程中，学生通过经历“坍塌又重建”的过程，积累了更为丰富的经验，这可助力其构建更为完整的知识体系.在初中数学解题教学中，教师应引导学生学会思考，培养其逻辑思维能力，不断提高学生分析问题和解决问题的能力.

参考文献：［1］ 闫惠泽.基于波利亚解题思想的高中数学公式的教学研究［D］.大连：辽宁师范大学，2020.

［2］ 李晶.例谈波利亚“怎样解题”表在初中数学解题中的应用［J］.数学教学通讯，2011（6）：20-22.

［3］ G·波利亚.怎样解题［M］.闫育苏，译.北京：科学出版社，1982.

［责任编辑：李 璟］