大概念视角下初中数学单元教学策略研究

摘 要：在初中数学教学中，开展基于大概念视角下的单元教学，有助于提高学生的整体思维与综合能力，能够切实推动数学课堂的高效建设.基于此，文章从建构“问题链”、把握“探究链”、设计“迁移链”三个维度探究实施单元教学的有效策略，让大概念经历“引出”“融入”“应用”的过程，以保证数学单元教学的有效性.

关键词：初中数学；大概念；单元教学；策略

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2024）29-0065-03

收稿日期：2024-07-15

作者简介：赵琳（1981.9—），女，甘肃省宕昌人，本科，中小学高级教师，从事初中数学教学研究.

大概念是指知识深处的底层逻辑和核心思想，是对知识间内在关系规律的高度概括.而单元教学是指以整段教学内容为框架，以课程目标为指导，以学生认知发展规律为基础，以单元主题为线索而开展的教学活动.在大概念视角下开展单元教学，能够进一步推动数学课堂教学内容的有效整合，让知识间的关联更为紧密，形成不可分割的教学整体.这样，学生的数学综合能力便可获得全面提升，数学教学效果也会得到有效提高.

1 建构“问题链”，引出大概念

“问题”是单元教学的核心，也是学生高效学习数学知识的动力［1］.大概念是对事实的抽象与概括，为了使学生理解大概念，实现对数学事实的有效认知，教师可采取建构“问题链”的方式展开教学活动，由此有效引出大概念，让学生从具体问题出发，系统思考单元知识［2］.笔者以人教版七年级数学上册第二章《整式的加减》为例，开展单元教学分析.

1.1 以问题为载体，呈现单元大概念

在《整式的加减》单元教学中，教师需要组织学生完成对“整式”“整式的加减”两部分内容的学习.为了有效呈现单元大概念，教师可以以问题为载体，设计连续性的思考问题，以此呈现单元大概念，帮助学生实现对大概念的理解，使其有效掌握单元知识，从而提高课堂教学效果.

在设计思考问题时，教师需要围绕“整式”这一大概念进行思考.一方面，在理解“整式”前，教师需要清楚地介绍“用字母表示数”“列式表示数量关系”“单项式”“多项式”等知识点；另一方面，需要具体介绍“合并同类项”“去括号”等知识点，并完成“整式的加减运算”的教学.基于上述知识，在初中数学教学中，教师可以设置具体的数学问题，让学生能够以问题为载体，深入理解单元知识［3］.至此，教师完成了以问题的形式呈现单元知识的过程，且可以按照具体的问题组织学生开展对单元大概念“整式”的学习，让学生通过理解具体的单元知识点，完成对大概念的认识和掌握.

由此可以看出，在初中数学教学过程中，教师系统地整理“整式的加减”单元知识，并将其转变为具体的思考问题，可以帮助学生进一步理解单元知识，使其有效认知单元大概念，从而提高学生分析问题和解决问题的能力.

1.2 以逻辑为基线，解释单元大概念

在完成“以问题为载体呈现单元知识”后，教师应依照知识的内在逻辑，组织学生开展对“整式的加减”知识的具体学习.在数学课堂中，教师需要以“知识间的逻辑关系”为基线，继续通过“设置思考问题”的方式，进一步阐述单元大概念，让学生做到对“整式”知识的有效思考、扎实掌握［4］.这样，当学生完成单元知识学习后，便可构建一定的知识体系，实现逻辑思维能力的提升.

比如，在学习“整式的加减”时，教师便需要按照“先合并同类项，再去括号，最后加减运算”的逻辑过程开展单元教学活动，让学生有效理解单元大概念.首先，教师需从具体数学问题入手，引导学生学习“合并同类项”的有关知识.

问题1 运用有理数的运算律计算下列各题：

（1）100×2+252×2；

（2）100×（-2）+252×（-2）.

问题2 根据问题1中的方法，计算100 t+252 t，并说明理由.

问题3 根据问题2中的结论，计算下列各题：

（1）3+2； （2）3a-4a； （3）100 t-252 t.

基于这些数学问题，教师可让学生思考这些运算之间的共同特点，让其从中总结规律.由此，教师便可以引导学生认识“同类项”“合并同类项”的概念.其次，教师需要提高知识学习难度，带领学生思考如何化简带有括号的整式.同样，教师可先让学生思考问题，如利用乘法分配律计算12×（13-16），（-6）×（12-13）.然后根据这一解题过程，计算+（x+3），-（x+3），2（x+8）等.在计算时，学生需思考去括号的方法.通过以上问题，学生能够有效掌握去括号的有关知识.最后，教师可以设置具体的整式加减运算，强化学生对整式加减知识的理解.

在上述单元教学过程中，教师按照知识的内在逻辑组织学生学习与思考单元知识，并完成对单元知识的有效运用.这样既充分呈现了单元大概念，也让学生对大概念有了具体的认识和掌握，有助于提高学生认知能力和思考能力.

2 把握“探究链”，融入大概念

大概念与单元核心知识有所不同，大概念是具有高度概括性的内容，而单元核心知识则是具体的知识点［5］.基于此，为了在单元整体教学中有效融入大概念，教师可采取设置“探究链”的方式，激活学生的探究思维，让学生产生探索大概念的兴趣，以此提高学生对单元数学知识的认知与思考.笔者以人教版七年级数学下册《相交线与平行线》单元为例，进行单元教学分析.

2.1 串接单元知识，开启探究大门

在《相交线与平行线》单元教学中，教师需要引导学生思考相交线的相关概念、平行线的判定、平行线的性质及平移等知识.在具体讲授这些内容时，教师需要抓住单元大概念，即思考相交线与平行线，就是思考两条无限延长的线是否会相交.在此基础上，教师可以设置具体的探究任务，并借此做到有效串接单元知识内容，锻炼学生的探究能力.

2.2 落实深度学习，实现深入探究

在完成设计“探究链”后，教师需要组织学生进行具体且深入学习，让学生深度掌握单元知识.在进行具体的单元教学过程中，教师应借助对探究任务的分析与解决，营造出积极探究的课堂氛围，让学生有效探究课程任务.在深入探究的过程中，完成对单元知识的深度学习与思考.

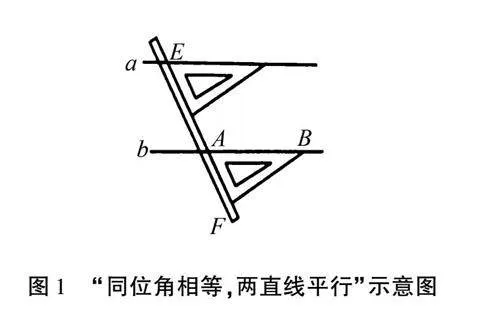
在学习“探究平行线及其相关知识”这部分单元内容时，可组织学生探究平行线的判定方法，落实深度学习.在探究过程中，教师可采取“先结合案例讲授判定方法，再组织学生自主应用探究”的方式，以此使学生实现深度学习.首先，教师需要讲授平行线有哪些判定方法，比如，经过直线外一点，有且只有一条直线与这条直线平行；同一平面内，两条直线垂直于同一条直线，则这两条直线平行；同位角相等，两直线平行.在讲授案例时，教师需要一边讲授，一边用案例图示进行展示.例如，在理解“同位角相等，两直线平行”时，教师可展示图1，并向学生详细说明判定方法.

在学生完成探究任务后，为了进一步强化学生对判定方法的掌握，教师可为学生布置一定的练习内容.

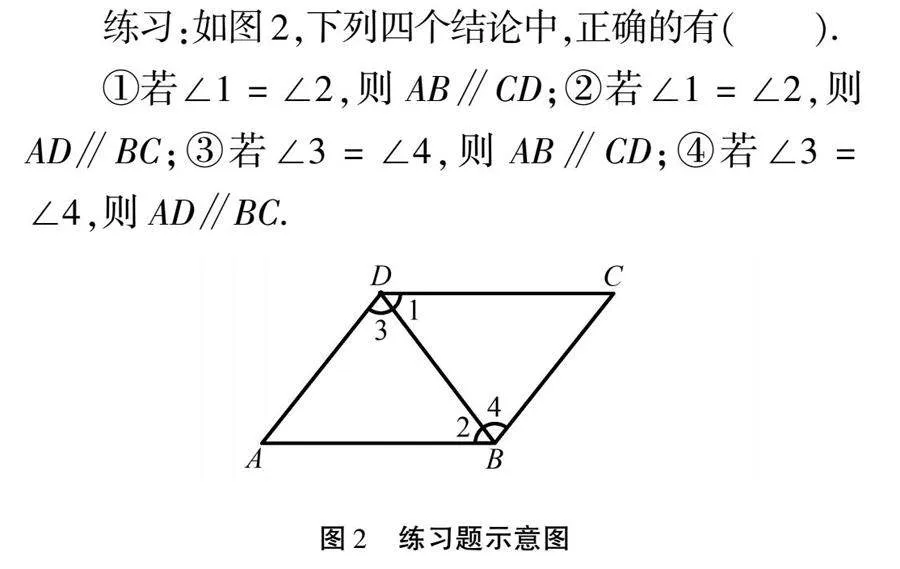
练习：如图2，下列四个结论中，正确的有（ ）.

①若∠1=∠2，则AB∥CD；②若∠1=∠2，则AD∥BC；③若∠3=∠4，则AB∥CD；④若∠3=∠4，则AD∥BC.

除选择题之外，还可以设置一些几何证明问题，提高学生运用所学知识分析问题和解决问题的能力.至此，教师组织学生完成了对所学知识的理解和思考，实现了对单元知识的深度学习，从而扎实掌握平行线的判定方法.

3 设计“迁移链”，应用大概念

培养学生的知识迁移与运用能力，是开展单元教学活动应达成的重要目标.基于此，在开展大概念视角下的单元教学活动时，教师应树立“为迁移而教”的教学思想，并通过设计“迁移链”的方式，引导学生有效应用大概念，从而提升单元教学成效.

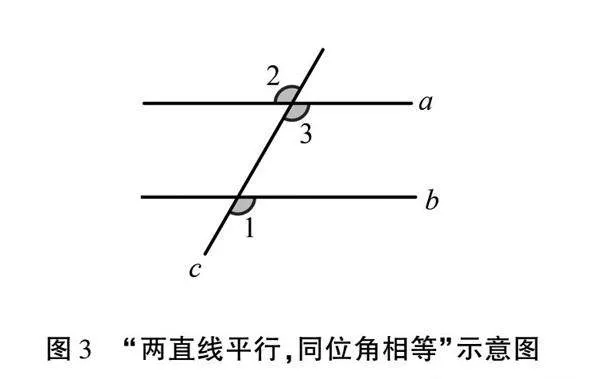
在《相交线与平行线》单元教学中，教师指导学生学习了平行线的判定方法后，需组织学生运用平行线判定解决实际问题.在解决问题过程中，教师需设计“迁移链”，组织学生对已掌握的知识进行迁移运用.比如，学生已理解“同位角相等，两直线平行”的判定方法，若对其进行反向思考，“两直线平行，同位角相等”，这个结论是否成立？学生思考、探究结束后，教师可列举具体的几何问题，让学生进一步思考，加深对所学知识的理解.比如，如图3，直线a∥b，c是截线，若∠1=120°，求∠2的度数.

根据平行线的性质，学生易知∠3=∠1=120°，而∠2和∠3是对顶角，即∠2=∠3=120°.用同样的方法，教师可组织学生完成对其余平行线性质的应用思考.这样，教师便组织学生在课堂学习中完成了对平行线性质知识的深度学习.在开展教学活动的过程中，教师借助设计“迁移链”的方式，组织学生深入思考单元大概念，并组织学生进行实际应用，以此强化学生对平行线知识的充分掌握，提高其运用平行线知识分析问题和解决问题的能力.

4 结束语

在初中数学教学中，教师应充分理解大概念思想，思考大概念为数学教学带来的益处.在教学过程中应合理开展单元教学，让数学知识的联系更为紧密，使单元教学能够在大概念的引领下不断提高教学效率，提高学生分析问题和解决问题的能力，提升学生的数学核心素养.

参考文献：［1］ 王婷.大概念视角下小学数学单元教学实践研究：以“乘法”单元为例［J］.理科爱好者，2023（6）：209-211.

［2］ 涂望星.大概念视角下的初中数学单元整体教学设计：以“一次函数”为例［J］.中学课程辅导，2023（36）：48-50.

［3］ 杨倩.大概念视角下的初中数学单元教学设计［J］.初中数学教与学，2023（18）：15-18.

［4］ 王洁.大概念视角下小学数学单元整体教学：以“生活中的负数”单元教学为例［J］.新教育，2023（26）：36-38.

［5］ 支耀红.基于学科大概念视角的初中数学单元整体教学设计的策略研究［J］.天天爱科学（教学研究），2023（6）：75-77.

［责任编辑：李 璟］